| ||||
|---|---|---|---|---|
| Cardinal | fifteen | |||
| Ordinal | 15th (fifteenth) | |||
| Numeral system | pentadecimal | |||
| Factorization | 3 × 5 | |||
| Divisors | 1, 3, 5, 15 | |||
| Greek numeral | ΙΕ´ | |||
| Roman numeral | XV | |||
| Binary | 11112 | |||
| Ternary | 1203 | |||
| Senary | 236 | |||
| Octal | 178 | |||
| Duodecimal | 1312 | |||
| Hexadecimal | F16 | |||
| Hebrew | ט"ו (Tet Vav) | |||
15 (fifteen) is the natural number following 14 and preceding 16.
Mathematics
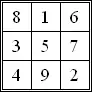
M = 15
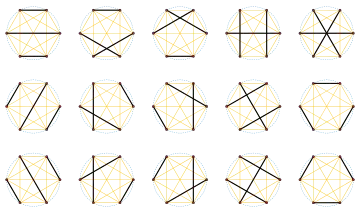
The 15 perfect matchings of K6
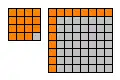
15 as the difference of two positive squares (in orange).
15 is:
- The eighth composite number and the sixth semiprime and the first odd and fourth discrete semiprime;[1] its proper divisors are 1, 3, and 5, so the first of the form (3.q),[2] where q is a higher prime.
- a deficient number, a lucky number, a bell number (i.e., the number of partitions for a set of size 4), [3] a pentatope number, [4] and a repdigit in binary (1111) and quaternary (33). In hexadecimal, and higher bases, it is represented as F.
- with an aliquot sum of 9; within an aliquot sequence of three composite numbers (15,9,4,3,1,0) to the Prime in the 3-aliquot tree.
- the second member of the first cluster of two discrete semiprimes (14, 15); the next such cluster is (21, 22).
- the first number to be polygonal in 3 ways: it is a triangular number, a hexagonal number,[5] and pentadecagonal number.[6]
- a centered tetrahedral number.
- the number of partitions of 7.
- the smallest number that can be factorized using Shor's quantum algorithm.
- the magic constant of the unique order-3 normal magic square.
- the number of supersingular primes.
- the smallest positive number that can be expressed as the difference of two positive squares in more than one way:[7] or (see image).
Furthermore,
- 15's prime factors, (3 and 5), form the first twin-prime pair.
- The first 15 superabundant numbers are the same as the first 15 colossally abundant numbers.
- In decimal, 15 contains the digits 1 and 5 and is the result of adding together the integers from 1 to 5 (1 + 2 + 3 + 4 + 5 = 15). The only other number with this property (in decimal) is 27.
- There are 15 truncatable primes that are both right-truncatable and left-truncatable:
- There are 15 perfect matchings of the complete graph K6 and 15 rooted binary trees with four labeled leaves, both of these being among the types of objects counted by double factorials.
- With only two exceptions, all prime quadruplets enclose a multiple of 15, with 15 itself being enclosed by the quadruplet (11, 13, 17, 19).
- If a positive definite quadratic form with integer matrix represents all positive integers up to 15, then it represents all positive integers via the 15 and 290 theorems.
- 15 is the product of distinct Fermat primes, 3 and 5; hence, a regular pentadecagon is constructible with a compass and unmarked straightedge, and is expressible in terms of square roots.
- There are 15 monohedral convex pentagonal tilings, with eight being edge-to-edge.
- There are 15 regular and semiregular tilings when infinite (improper) apeirogonal forms are counted: three are regular (with one self-dual), eight are semiregular (with one chiral), and four are apeirogonal (from a total of 8, in-which 4 are duplicates).
- Full icosahedral symmetry contains 15 mirror planes (2-fold axes). Specifically, the symmetry order for both the regular icosahedron and regular dodecahedron (which is made of regular pentagons) is 120: equal to sum of the first 15 integers, and the factorial of 5, wherein the sum of the first 5 integers itself is 15. Expressed mathematically:
- , while , and .
- There are 15 Archimedean solids and 15 Catalan solids when enantiomorphic forms are counted separately.
- There are 15 regular honeycombs in hyperbolic 3-space: four are compact, and 11 are paracompact.[8]
- It is the smallest non-trivial Surprise Number. When 15 is partitioned into 2 parts of digits- smaller part 1 and larger part 5, adding numbers from smaller 1 to larger 5 = 1 + 2 + 3 + 4 + 5 = 15 = Original Number.
Science

- The atomic number of phosphorus.
- 15 Eunomia is the largest Eunomian asteroid in the inner asteroid belt.
Religion
Sunnism
The Hanbali Sunni madhab states that the age of fifteen of a solar or lunar calendar is when one's taklif (obligation or responsibility) begins and is the stage whereby one has his deeds recorded.[9]
Judaism
- In the Hebrew numbering system, the number 15 is not written according to the usual method, with the letters that represent "10" and "5" (י-ה, yodh and heh), because those spell out one of the Jewish names of God. Instead, the date is written with the letters representing "9" and "6" (ט-ו, teth and vav)
References
- ↑ Sloane, N. J. A. (ed.). "Sequence A001358 (Semiprimes (or biprimes): products of two primes.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ Sloane, N. J. A. (ed.). "Sequence A001748 (a(n) = 3 * prime(n))". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ Sloane, N. J. A. (ed.). "Sequence A000110 (Bell or exponential numbers)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ Sloane, N. J. A. (ed.). "Sequence A000332 (Binomial coefficient binomial(n,4) = n*(n-1)*(n-2)*(n-3)/24)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ Sloane, N. J. A. (ed.). "Sequence A000384 (Hexagonal numbers)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ Sloane, N. J. A. (ed.). "Sequence A051867 (pentadecagonal numbers.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ Sloane, N. J. A. (ed.). "Sequence A334078 (a(n) is the smallest positive integer that can be expressed as the difference of two positive squares in at least n ways.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ H.S.M. Coxeter (1954). "Regular Honeycombs in Hyperbolic Space". Proceedings of the International Congress of Mathematicians. 3: 155–169. CiteSeerX 10.1.1.361.251.
- ↑ Spevack, Aaron (2011). Ghazali on the Principles of Islamic Spiritualit. p. 50.
Further reading
- Wells, D. The Penguin Dictionary of Curious and Interesting Numbers London: Penguin Group. (1987): 91–93
External links
Look up 15 in Wiktionary, the free dictionary.
- Clewett, James. "15: f in hexadecimal". Numberphile. Brady Haran. Archived from the original on 2013-05-16. Retrieved 2013-04-02. – discussing hexadecimals
- Bowley, Roger. "15: Bumfit". Numberphile. Brady Haran. Archived from the original on 2013-05-16. Retrieved 2013-04-01. – discussing the Celtic number as used in Lincolnshire
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.