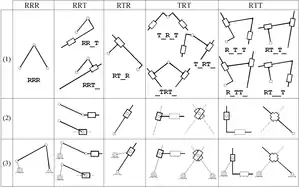
In kinematics, an Assur group is a kinematic chain with zero degree of mobility, which added or subtracted from a mechanism do not alter its original number of degrees of freedom. They have been first described by the Russian engineer Leonid Assur (1878–1920) in 1914.[2][3]
The simplest of all Assur groups (also known as dyads) have two links and three joints, of which two are potential joints. Using an underscore "_" to indicate a guide following or preceding a slider in a translating (prismatic) joint, all possible dyadic isomers will be: RRR, RR_T, RRT_, RT_R, T_R_T, T_RT_, _TRT_, R_T_T, R_T_T, RT_T_, R_TT_ and RT__T.
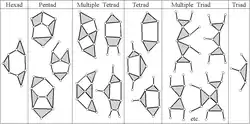
Higher order Assur groups are known such as simple and multiple triads, simple and multiple thertad, pentad hexad etc.
When an Assur group is connected to the same link, zero degree-of-freedom entities known as Baranov trusses are obtained.
MechDesigner from PSMotion, OSMEC from ESDU and MeKin2D are software programs known to use Assur group/modular approach for the motion analysis of planar linkage mechanisms.
See also
References
- ↑ Simionescu, P.A. (2014). Computer Aided Graphing and Simulation Tools for AutoCAD Users (1st ed.). Boca Raton, FL: CRC Press. ISBN 978-1-4822-5290-3.
- ↑ Assur, L. (1914). "Research of a planar linkages with lower pairs on the basis of their structure and classification". Proceedings of Saint-Petersburg Polytechnic Institute. 20–21.
- ↑ Evgrafov, A.; Kozlikin, D. (2014). "Leonid Assur (1878–1920)". In Ceccarelli, M. (ed.). Distinguished Figures in Mechanism and Machine Science: Their Contributions and Legacies. History of Mechanism and Machine Science. Vol. 26. Dordrecht: Springer. doi:10.1007/978-94-017-8947-9_2.