Barlow's formula (called "Kesselformel"[1] in German) relates the internal pressure that a pipe[2] can withstand to its dimensions and the strength of its material. This approximate formula is named after Peter Barlow, an English mathematician.[3]

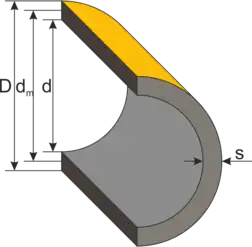Cylinder
,

where

 : internal pressure,
 : allowable stress,
  : wall thickness,
 : outside diameter.

This formula (DIN 2413) figures prominently in the design of autoclaves and other pressure vessels.

Other formulations

The design of a complex pressure containment system involves much more than the application of Barlow's formula. For example, in 100 countries the ASME BPVCcode stipulates the requirements for design and testing of pressure vessels.[4]

The formula is also common in the pipeline industry to verify that pipe used for gathering, transmission, and distribution lines can safely withstand operating pressures. The design factor is multiplied by the resulting pressure which gives the maximum operating pressure (MAOP) for the pipeline. In the United States, this design factor is dependent on Class locations which are defined in DOT Part 192. There are four class locations corresponding to four design factors:[5]

Class Definition Design
factor
1An offshore area or any class location unit that has 10 or fewer buildings intended for human occupancy0.72
2Any class location that has more than 10 but fewer than 46 buildings intended for human occupancy0.60
3Any location that has 46 or more buildings intended for human occupancy or any area where the pipeline lies within 100 yards (91 meters) of a building or a small, well-defined outdoor area (such as a playground, recreation area, outdoor theater, or place of public assembly) that is occupied by 20 or more persons at least five days a week for 10 weeks in any 12-month period—weeks need not be consecutive0.50
4Any class location unit where buildings with four or more stories above the ground are prevalent0.40

References

  1. ↑ "Kesselformel", Wikipedia (in German), 2022-08-18, retrieved 2022-08-20
  2. ↑ Or pressure vessel, or other cylindrical pressure containment structure.
  3. ↑ Adams, A.J.; Grundy, K.C.; Lin, B.; Moore, PW. (6 March 2018). The Barlow Equation for Tubular Burst: A Muddled History. IADC/SPE Drilling Conference and Exhibition. Fort Worth, Texas, USA. pp. SPE-189681-MS. doi:10.2118/189681-MS.
  4. ↑ "2017 Boiler and Pressure Vessel Code: An International Code" (PDF). Retrieved 9 October 2021.
  5. ↑ "US Code of Regulations: Title 49, Subtitle B, Chapter I, Subchapter D, Part 192.5". Retrieved 9 October 2021.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.