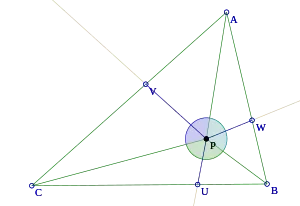
In geometry, Barrow's inequality is an inequality relating the distances between an arbitrary point within a triangle, the vertices of the triangle, and certain points on the sides of the triangle. It is named after David Francis Barrow.
Statement
Let P be an arbitrary point inside the triangle ABC. From P and ABC, define U, V, and W as the points where the angle bisectors of BPC, CPA, and APB intersect the sides BC, CA, AB, respectively. Then Barrow's inequality states that[1]
with equality holding only in the case of an equilateral triangle and P is the center of the triangle.[1]
Generalisation
Barrow's inequality can be extended to convex polygons. For a convex polygon with vertices let be an inner point and the intersections of the angle bisectors of with the associated polygon sides , then the following inequality holds:[2][3]
Here denotes the secant function. For the triangle case the inequality becomes Barrow's inequality due to .
History
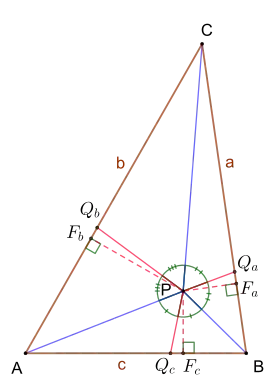
Barrow's inequality strengthens the Erdős–Mordell inequality, which has identical form except with PU, PV, and PW replaced by the three distances of P from the triangle's sides. It is named after David Francis Barrow. Barrow's proof of this inequality was published in 1937, as his solution to a problem posed in the American Mathematical Monthly of proving the Erdős–Mordell inequality.[1] This result was named "Barrow's inequality" as early as 1961.[4]
A simpler proof was later given by Louis J. Mordell.[5]
See also
References
- 1 2 3 Erdős, Paul; Mordell, L. J.; Barrow, David F. (1937), "Solution to problem 3740", American Mathematical Monthly, 44 (4): 252–254, doi:10.2307/2300713, JSTOR 2300713.
- ↑ M. Dinca: "A Simple Proof of the Erdös-Mordell Inequality". In: Articole si Note Matematice, 2009
- ↑ Hans-Christof Lenhard: "Verallgemeinerung und Verschärfung der Erdös-Mordellschen Ungleichung für Polygone". In: Archiv für Mathematische Logik und Grundlagenforschung, Band 12, S. 311–314, doi:10.1007/BF01650566 (German).
- ↑ Oppenheim, A. (1961), "New inequalities for a triangle and an internal point", Annali di Matematica Pura ed Applicata, 53: 157–163, doi:10.1007/BF02417793, MR 0124774
- ↑ Mordell, L. J. (1962), "On geometric problems of Erdös and Oppenheim", The Mathematical Gazette, 46 (357): 213–215, JSTOR 3614019.