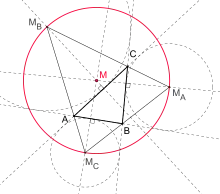
In geometry, the Bevan point, named after Benjamin Bevan, is a triangle center. It is defined as center of the Bevan circle, that is the circle through the centers of the three excircles of a triangle.
The Bevan point of a triangle is the reflection of the incenter across the circumcenter of the triangle.
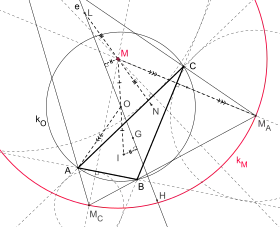
The Bevan point M of triangle △ABC has the same distance from its Euler line e as its incenter I and the circumcenter O is the midpoint of the line segment MI. The length of MI is given by
where R denotes the radius of the circumcircle and a, b, c the sides of △ABC. The Bevan is point is also the midpoint of the line segment NL connecting the Nagel point N and the de Longchamps point L. The radius of the Bevan circle is 2R, that is twice the radius of the circumcircle.
External links
- Eric W. Weisstein. Bevan Point. From MathWorld--A Wolfram Web Resource
- Alexander Bogomolny. Bevan's Point and Theorem at cut-the-knot
- Encyclopedia of Triangle Centers. X(40) = BEVAN POINT