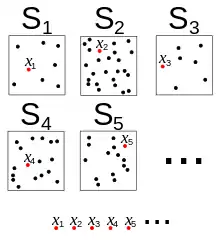
Each set in the countable sequence of sets (Si) = S1, S2, S3, ... contains a non-zero, and possibly infinite (or even uncountably infinite), number of elements. The axiom of countable choice allows us to arbitrarily select a single element from each set, forming a corresponding sequence of elements (xi) = x1, x2, x3, ...

The axiom of countable choice or axiom of denumerable choice, denoted ACω, is an axiom of set theory that states that every countable collection of non-empty sets must have a choice function. That is, given a function A with domain N (where N denotes the set of natural numbers) such that A(n) is a non-empty set for every n ∈ N, there exists a function f with domain N such that f(n) ∈ A(n) for every n ∈ N.

Overview

The axiom of countable choice (ACω) is strictly weaker than the axiom of dependent choice (DC), (Jech 1973) which in turn is weaker than the axiom of choice (AC). Paul Cohen showed that ACω is not provable in Zermelo–Fraenkel set theory (ZF) without the axiom of choice (Potter 2004). ACω holds in the Solovay model.

ZF+ACω suffices to prove that the union of countably many countable sets is countable. The converse statement "assuming ZF, 'every countable union of countable sets is countable' implies ACω" does not hold, as witnessed by Cohen's First Model.[1] ZF+ACω also suffices to prove that every infinite set is Dedekind-infinite (equivalently: has a countably infinite subset).

ACω is particularly useful for the development of analysis, where many results depend on having a choice function for a countable collection of sets of real numbers. For instance, in order to prove that every accumulation point x of a set S ⊆ R is the limit of some sequence of elements of S \ {x}, one needs (a weak form of) the axiom of countable choice. When formulated for accumulation points of arbitrary metric spaces, the statement becomes equivalent to ACω. For other statements equivalent to ACω, see Herrlich (1997) and Howard & Rubin (1998).

A common misconception is that countable choice has an inductive nature and is therefore provable as a theorem (in ZF, or similar, or even weaker systems) by induction. However, this is not the case; this misconception is the result of confusing countable choice with finite choice for a finite set of size n (for arbitrary n), and it is this latter result (which is an elementary theorem in combinatorics) that is provable by induction. However, some countably infinite sets of non-empty sets can be proven to have a choice function in ZF without any form of the axiom of choice. For example, Vω − {Ø} has a choice function, where Vω is the set of hereditarily finite sets, i.e. the first set in the Von Neumann universe of non-finite rank. The choice function is (trivially) the least element in the well-ordering. Another example is the set of proper and bounded open intervals of real numbers with rational endpoints.

Use

As an example of an application of ACω, here is a proof (from ZF + ACω) that every infinite set is Dedekind-infinite:

Let X be infinite. For each natural number n, let An be the set of all 2n-element subsets of X. Since X is infinite, each An is non-empty. The first application of ACω yields a sequence (Bn : n = 0,1,2,3,...) where each Bn is a subset of X with 2n elements.
The sets Bn are not necessarily disjoint, but we can define
C0 = B0
Cn = the difference between Bn and the union of all Cj, j < n.
Clearly each set Cn has at least 1 and at most 2n elements, and the sets Cn are pairwise disjoint. The second application of ACω yields a sequence (cn: n = 0,1,2,...) with cn ∈ Cn.
So all the cn are distinct, and X contains a countable set. The function that maps each cn to cn+1 (and leaves all other elements of X fixed) is a 1-1 map from X into X which is not onto, proving that X is Dedekind-infinite.

References

  1. ↑ Herrlich, Horst (2006). Axiom of Choice. Section A.4: Springer. ISBN 3-540-30989-6. Retrieved 18 July 2023.{{cite book}}: CS1 maint: location (link)

This article incorporates material from axiom of countable choice on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.