D* (pronounced "D star") is any one of the following three related incremental search algorithms:
- The original D*,[1] by Anthony Stentz, is an informed incremental search algorithm.
- Focused D*[2] is an informed incremental heuristic search algorithm by Anthony Stentz that combines ideas of A*[3] and the original D*. Focused D* resulted from a further development of the original D*.
- D* Lite[4] is an incremental heuristic search algorithm by Sven Koenig and Maxim Likhachev that builds on LPA*,[5] an incremental heuristic search algorithm that combines ideas of A* and Dynamic SWSF-FP.[6]
All three search algorithms solve the same assumption-based path planning problems, including planning with the freespace assumption,[7] where a robot has to navigate to given goal coordinates in unknown terrain. It makes assumptions about the unknown part of the terrain (for example: that it contains no obstacles) and finds a shortest path from its current coordinates to the goal coordinates under these assumptions. The robot then follows the path. When it observes new map information (such as previously unknown obstacles), it adds the information to its map and, if necessary, replans a new shortest path from its current coordinates to the given goal coordinates. It repeats the process until it reaches the goal coordinates or determines that the goal coordinates cannot be reached. When traversing unknown terrain, new obstacles may be discovered frequently, so this replanning needs to be fast. Incremental (heuristic) search algorithms speed up searches for sequences of similar search problems by using experience with the previous problems to speed up the search for the current one. Assuming the goal coordinates do not change, all three search algorithms are more efficient than repeated A* searches.
D* and its variants have been widely used for mobile robot and autonomous vehicle navigation. Current systems are typically based on D* Lite rather than the original D* or Focused D*. In fact, even Stentz's lab uses D* Lite rather than D* in some implementations.[8] Such navigation systems include a prototype system tested on the Mars rovers Opportunity and Spirit and the navigation system of the winning entry in the DARPA Urban Challenge, both developed at Carnegie Mellon University.
The original D* was introduced by Anthony Stentz in 1994. The name D* comes from the term "Dynamic A*",[9] because the algorithm behaves like A* except that the arc costs can change as the algorithm runs.
Operation
The basic operation of D* is outlined below.
Like Dijkstra's algorithm and A*, D* maintains a list of nodes to be evaluated, known as the "OPEN list". Nodes are marked as having one of several states:
- NEW, meaning it has never been placed on the OPEN list
- OPEN, meaning it is currently on the OPEN list
- CLOSED, meaning it is no longer on the OPEN list
- RAISE, indicating its cost is higher than the last time it was on the OPEN list
- LOWER, indicating its cost is lower than the last time it was on the OPEN list
Expansion
The algorithm works by iteratively selecting a node from the OPEN list and evaluating it. It then propagates the node's changes to all of the neighboring nodes and places them on the OPEN list. This propagation process is termed "expansion". In contrast to canonical A*, which follows the path from start to finish, D* begins by searching backwards from the goal node. This means that the algorithm is actually computing the A* optimal path for every possible start node.[10] Each expanded node has a backpointer which refers to the next node leading to the target, and each node knows the exact cost to the target. When the start node is the next node to be expanded, the algorithm is done, and the path to the goal can be found by simply following the backpointers.
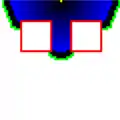 Expansion in progress. The finish node (yellow) is in the middle of the top row of points, the start node is in the middle of the bottom row. Red indicates an obstacle; black/blue indicates expanded nodes (brightness indicating cost). Green indicates nodes which are being expanded.
Expansion in progress. The finish node (yellow) is in the middle of the top row of points, the start node is in the middle of the bottom row. Red indicates an obstacle; black/blue indicates expanded nodes (brightness indicating cost). Green indicates nodes which are being expanded. Expansion finished. The path is indicated in cyan.
Expansion finished. The path is indicated in cyan.
Obstacle handling
When an obstruction is detected along the intended path, all the points that are affected are again placed on the OPEN list, this time marked RAISE. Before a RAISED node increases in cost, however, the algorithm checks its neighbors and examines whether it can reduce the node's cost. If not, the RAISE state is propagated to all of the nodes' descendants, that is, nodes which have backpointers to it. These nodes are then evaluated, and the RAISE state is passed on, forming a wave. When a RAISED node can be reduced, its backpointer is updated, and passes the LOWER state to its neighbors. These waves of RAISE and LOWER states are the heart of D*.
By this point, a whole series of other points are prevented from being "touched" by the waves. The algorithm has therefore only worked on the points which are affected by change of cost.
 An obstacle has been added (red) and nodes marked RAISE (yellow).
An obstacle has been added (red) and nodes marked RAISE (yellow). Expansion in progress. Yellow indicates nodes marked RAISE, green indicates nodes marked LOWER.
Expansion in progress. Yellow indicates nodes marked RAISE, green indicates nodes marked LOWER.
Another deadlock occurs
This time, the deadlock cannot be bypassed so elegantly. None of the points can find a new route via a neighbor to the destination. Therefore, they continue to propagate their cost increase. Only points outside of the channel can be found, which can lead to destination via a viable route. This is how two Lower waves develop, which expand as points marked as unattainable with new route information.
 Channel blocked by additional obstacles (red)
Channel blocked by additional obstacles (red) Expansion in progress (Raise wave in yellow, Lower wave in green)
Expansion in progress (Raise wave in yellow, Lower wave in green) New path found (cyan)
New path found (cyan)
Pseudocode
while (!openList.isEmpty()) {
point = openList.getFirst();
expand(point);
}
Expand
void expand(currentPoint) {
boolean isRaise = isRaise(currentPoint);
double cost;
for each (neighbor in currentPoint.getNeighbors()) {
if (isRaise) {
if (neighbor.nextPoint == currentPoint) {
neighbor.setNextPointAndUpdateCost(currentPoint);
openList.add(neighbor);
} else {
cost = neighbor.calculateCostVia(currentPoint);
if (cost < neighbor.getCost()) {
currentPoint.setMinimumCostToCurrentCost();
openList.add(currentPoint);
}
}
} else {
cost = neighbor.calculateCostVia(currentPoint);
if (cost < neighbor.getCost()) {
neighbor.setNextPointAndUpdateCost(currentPoint);
openList.add(neighbor);
}
}
}
}
Check for raise
boolean isRaise(point) {
double cost;
if (point.getCurrentCost() > point.getMinimumCost()) {
for each(neighbor in point.getNeighbors()) {
cost = point.calculateCostVia(neighbor);
if (cost < point.getCurrentCost()) {
point.setNextPointAndUpdateCost(neighbor);
}
}
}
return point.getCurrentCost() > point.getMinimumCost();
}
Variants
Focused D*
As its name suggests, Focused D* is an extension of D* which uses a heuristic to focus the propagation of RAISE and LOWER toward the robot. In this way, only the states that matter are updated, in the same way that A* only computes costs for some of the nodes.
D* Lite
D* Lite is not based on the original D* or Focused D*, but implements the same behavior. It is simpler to understand and can be implemented in fewer lines of code, hence the name "D* Lite". Performance-wise, it is as good as or better than Focused D*. D* Lite is based on Lifelong Planning A*, which was introduced by Koenig and Likhachev few years earlier. D* Lite
Minimum cost versus current cost
For D*, it is important to distinguish between current and minimum costs. The former is only important at the time of collection and the latter is critical because it sorts the OpenList. The function which returns the minimum cost is always the lowest cost to the current point since it is the first entry of the OpenList.
References
- ↑ Stentz, Anthony (1994), "Optimal and Efficient Path Planning for Partially-Known Environments", Proceedings of the International Conference on Robotics and Automation: 3310–3317, CiteSeerX 10.1.1.15.3683
- ↑ Stentz, Anthony (1995), "The Focussed D* Algorithm for Real-Time Replanning", Proceedings of the International Joint Conference on Artificial Intelligence: 1652–1659, CiteSeerX 10.1.1.41.8257
- ↑ Hart, P.; Nilsson, N.; Raphael, B. (1968), "A Formal Basis for the Heuristic Determination of Minimum Cost Paths", IEEE Transactions on Systems Science and Cybernetics, SSC-4 (2): 100–107, doi:10.1109/TSSC.1968.300136
- ↑ Koenig, S.; Likhachev, M. (2005), "Fast Replanning for Navigation in Unknown Terrain", IEEE Transactions on Robotics, 21 (3): 354–363, CiteSeerX 10.1.1.65.5979, doi:10.1109/tro.2004.838026, S2CID 15664344
- ↑ Koenig, S.; Likhachev, M.; Furcy, D. (2004), "Lifelong Planning A*", Artificial Intelligence, 155 (1–2): 93–146, doi:10.1016/j.artint.2003.12.001
- ↑ Ramalingam, G.; Reps, T. (1996), "An incremental algorithm for a generalization of the shortest-path problem", Journal of Algorithms, 21 (2): 267–305, CiteSeerX 10.1.1.3.7926, doi:10.1006/jagm.1996.0046
- ↑ Koenig, S.; Smirnov, Y.; Tovey, C. (2003), "Performance Bounds for Planning in Unknown Terrain", Artificial Intelligence, 147 (1–2): 253–279, doi:10.1016/s0004-3702(03)00062-6
- ↑ Wooden, D. (2006). Graph-based Path Planning for Mobile Robots (Thesis). Georgia Institute of Technology.
- ↑ Stentz, Anthony (1995), "The Focussed D* Algorithm for Real-Time Replanning", Proceedings of the International Joint Conference on Artificial Intelligence: 1652–1659, CiteSeerX 10.1.1.41.8257
- ↑ Murphy, Robin R. (2019). Introduction to AI robotics (2nd ed.). Bradford Books. Paragraph 14.5.2. ISBN 978-0262038485.