Jacobi elliptic functions

In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions. They are found in the description of the motion of a pendulum (see also pendulum (mathematics)), as well as in the design of electronic elliptic filters. While trigonometric functions are defined with reference to a circle, the Jacobi elliptic functions are a generalization which refer to other conic sections, the ellipse in particular. The relation to trigonometric functions is contained in the notation, for example, by the matching notation $\operatorname {sn}$ for $\sin$ . The Jacobi elliptic functions are used more often in practical problems than the Weierstrass elliptic functions as they do not require notions of complex analysis to be defined and/or understood. They were introduced by Carl Gustav Jakob Jacobi (1829). Carl Friedrich Gauss had already studied special Jacobi elliptic functions in 1797, the lemniscate elliptic functions in particular,^[1] but his work was published much later.

Overview

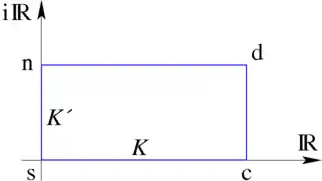
The fundamental rectangle in the complex plane of

u

There are twelve Jacobi elliptic functions denoted by $\operatorname {pq} (u,m)$ , where $\mathrm {p}$ and $\mathrm {q}$ are any of the letters $\mathrm {c}$ , $\mathrm {s}$ , $\mathrm {n}$ , and $\mathrm {d}$ . (Functions of the form $\operatorname {pp} (u,m)$ are trivially set to unity for notational completeness.) $u$ is the argument, and $m$ is the parameter, both of which may be complex. In fact, the Jacobi elliptic functions are meromorphic in both $u$ and $m$ .^[2] The distribution of the zeros and poles in the $u$ -plane is well-known. However, questions of the distribution of the zeros and poles in the $m$ -plane remain to be investigated.^[2]

In the complex plane of the argument $u$ , the twelve functions form a repeating lattice of simple poles and zeroes.^[3] Depending on the function, one repeating parallelogram, or unit cell, will have sides of length $2K$ or $4K$ on the real axis, and $2K'$ or $4K'$ on the imaginary axis, where $K=K(m)$ and $K'=K(1-m)$ are known as the quarter periods with $K(\cdot )$ being the elliptic integral of the first kind. The nature of the unit cell can be determined by inspecting the "auxiliary rectangle" (generally a parallelogram), which is a rectangle formed by the origin $(0,0)$ at one corner, and $(K,K')$ as the diagonally opposite corner. As in the diagram, the four corners of the auxiliary rectangle are named $\mathrm {s}$ , $\mathrm {c}$ , $\mathrm {d}$ , and $\mathrm {n}$ , going counter-clockwise from the origin. The function $\operatorname {pq} (u,m)$ will have a zero at the $\mathrm {p}$ corner and a pole at the $\mathrm {q}$ corner. The twelve functions correspond to the twelve ways of arranging these poles and zeroes in the corners of the rectangle.

When the argument $u$ and parameter $m$ are real, with $0<m<1$ , $K$ and $K'$ will be real and the auxiliary parallelogram will in fact be a rectangle, and the Jacobi elliptic functions will all be real valued on the real line.

Since the Jacobian elliptic functions are doubly periodic in $u$ , they factor through a torus – in effect, their domain can be taken to be a torus, just as cosine and sine are in effect defined on a circle. Instead of having only one circle, we now have the product of two circles, one real and the other imaginary. The complex plane can be replaced by a complex torus. The circumference of the first circle is $4K$ and the second $4K'$ , where $K$ and $K'$ are the quarter periods. Each function has two zeroes and two poles at opposite positions on the torus. Among the points $0$ , $K$ , $K+iK'$ , $iK'$ there is one zero and one pole.

The Jacobian elliptic functions are then doubly periodic, meromorphic functions satisfying the following properties:

There is a simple zero at the corner $\mathrm {p}$ , and a simple pole at the corner $\mathrm {q}$ .
The complex number $\mathrm {p} -\mathrm {q}$ is equal to half the period of the function $\operatorname {pq} u$ ; that is, the function $\operatorname {pq} u$ is periodic in the direction $\operatorname {pq}$ , with the period being $2(\mathrm {p} -\mathrm {q} )$ . The function $\operatorname {pq} u$ is also periodic in the other two directions $\mathrm {pp} '$ and $\mathrm {pq} '$ , with periods such that $\mathrm {p} -\mathrm {p} '$ and $\mathrm {p} -\mathrm {q} '$ are quarter periods.

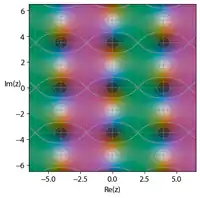
$alt=Elliptic Jacobi function sn {\displaystyle \operatorname {sn} } , k = 0.8 {\displaystyle k=0.8}$

Jacobi elliptic function

\operatorname {sn}

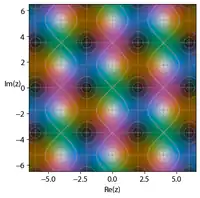
$alt=Elliptic Jacobi function cn {\displaystyle \operatorname {cn} } , k = 0.8 {\displaystyle k=0.8}$

Jacobi elliptic function

\operatorname {cn}

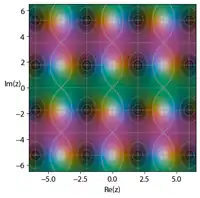
$alt=Elliptic Jacobi function dn {\displaystyle \operatorname {dn} } , k = 0.8 {\displaystyle k=0.8}$

Jacobi elliptic function

\operatorname {dn}

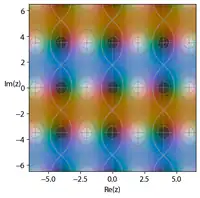
$alt=Elliptic Jacobi function sc {\displaystyle \operatorname {sc} } , k = 0.8 {\displaystyle k=0.8}$

Jacobi elliptic function

\operatorname {sc}

Plots of four Jacobi Elliptic Functions in the complex plane of

u

, illustrating their double periodic behavior. Images generated using a version of the domain coloring method.^[4] All have values of

k={\sqrt {m}}

equal to

0.8

.

Notation

The elliptic functions can be given in a variety of notations, which can make the subject unnecessarily confusing. Elliptic functions are functions of two variables. The first variable might be given in terms of the amplitude $\varphi$ , or more commonly, in terms of $u$ given below. The second variable might be given in terms of the parameter $m$ , or as the elliptic modulus $k$ , where $k^{2}=m$ , or in terms of the modular angle $\alpha$ , where $m=\sin ^{2}\alpha$ . The complements of $k$ and $m$ are defined as $m'=1-m$ and ${\textstyle k'={\sqrt {m'}}}$ . These four terms are used below without comment to simplify various expressions.

The twelve Jacobi elliptic functions are generally written as $\operatorname {pq} (u,m)$ where $\mathrm {p}$ and $\mathrm {q}$ are any of the letters $\mathrm {c}$ , $\mathrm {s}$ , $\mathrm {n}$ , and $\mathrm {d}$ . Functions of the form $\operatorname {pp} (u,m)$ are trivially set to unity for notational completeness. The “major” functions are generally taken to be $\operatorname {cn} (u,m)$ , $\operatorname {sn} (u,m)$ and $\operatorname {dn} (u,m)$ from which all other functions can be derived and expressions are often written solely in terms of these three functions, however, various symmetries and generalizations are often most conveniently expressed using the full set. (This notation is due to Gudermann and Glaisher and is not Jacobi's original notation.)

Throughout this article, $\operatorname {pq} (u,t^{2})=\operatorname {pq} (u;t)$ .

The functions are notationally related to each other by the multiplication rule: (arguments suppressed)

\operatorname {pq} \cdot \operatorname {p'q'} =\operatorname {pq'} \cdot \operatorname {p'q}

from which other commonly used relationships can be derived:

{\frac {\operatorname {pr} }{\operatorname {qr} }}=\operatorname {pq}

\operatorname {pr} \cdot \operatorname {rq} =\operatorname {pq}

{\frac {1}{\operatorname {qp} }}=\operatorname {pq}

The multiplication rule follows immediately from the identification of the elliptic functions with the Neville theta functions^[5]

\operatorname {pq} (u,m)={\frac {\theta _{\operatorname {p} }(u,m)}{\theta _{\operatorname {q} }(u,m)}}

Also note that:

K(m)=K(k^{2})=\int _{0}^{1}{\frac {dt}{\sqrt {(1-t^{2})(1-mt^{2})}}}=\int _{0}^{1}{\frac {dt}{\sqrt {(1-t^{2})(1-k^{2}t^{2})}}}.

Definition in terms of inverses of elliptic integrals

Model of the Jacobi amplitude (measured along vertical axis) as a function of independent variables u and the modulus k

There is a definition, relating the elliptic functions to the inverse of the incomplete elliptic integral of the first kind. These functions take the parameters $u$ and $m$ as inputs. The $\varphi$ that satisfies

u=\int _{0}^{\varphi }{\frac {\mathrm {d} \theta }{\sqrt {1-m\sin ^{2}\theta }}}

is called the Jacobi amplitude:

\operatorname {am} (u,m)=\varphi .

In this framework, the elliptic sine sn u (Latin: sinus amplitudinis) is given by

\operatorname {sn} (u,m)=\sin \operatorname {am} (u,m)

and the elliptic cosine cn u (Latin: cosinus amplitudinis) is given by

\operatorname {cn} (u,m)=\cos \operatorname {am} (u,m)

and the delta amplitude dn u (Latin: delta amplitudinis)^{[note 1]}

\operatorname {dn} (u,m)={\frac {\mathrm {d} }{\mathrm {d} u}}\operatorname {am} (u,m).

In the above, the value $m$ is a free parameter, usually taken to be real such that $0\leq m\leq 1$ , and so the elliptic functions can be thought of as being given by two variables, $u$ and the parameter $m$ . The remaining nine elliptic functions are easily built from the above three ( $\operatorname {sn}$ , $\operatorname {cn}$ , $\operatorname {dn}$ ), and are given in a section below.

In the most general setting, $\operatorname {am} (u,m)$ is a multivalued function (in $u$ ) with infinitely many logarithmic branch points (the branches differ by integer multiples of $2\pi$ ), namely the points $2sK(m)+(4t+1)K(1-m)i$ and $2sK(m)+(4t+3)K(1-m)i$ where $s,t\in \mathbb {Z}$ .^[6] This multivalued function can be made single-valued by cutting the complex plane along the line segments joining these branch points (the cutting can be done in non-equivalent ways, giving non-equivalent single-valued functions), thus making $\operatorname {am} (u,m)$ analytic everywhere except on the branch cuts. In contrast, $\sin \operatorname {am} (u,m)$ and other elliptic functions have no branch points, give consistent values for every branch of $\operatorname {am}$ , and are meromorphic in the whole complex plane. Since every elliptic function is meromorphic in the whole complex plane (by definition), $\operatorname {am} (u,m)$ (when considered as a single-valued function) is not an elliptic function.

However, the integral inversion above defines a unique single-valued real-analytic function in a real neighborhood of $u=0$ if $m$ is real. There is a unique analytic continuation of this function from that neighborhood to $u\in \mathbb {R}$ . The analytic continuation of this function is periodic in $u$ if and only if $m>1$ (with the minimal period $4K(1/m)/{\sqrt {m}}$ ), and it is denoted by $\operatorname {am} (u,m)$ in the rest of this article.

Jacobi also introduced the coamplitude function:

\operatorname {coam} (u,m)=\operatorname {am} (K(m)-u,m)

.

The Jacobi epsilon function can be defined as^[7]

{\mathcal {E}}(u,m)=\int _{0}^{u}\operatorname {dn} ^{2}(t,m)\,\mathrm {d} t

and relates the incomplete elliptic integral of the first kind to the incomplete elliptic integral of the second kind (with parameter $m$ ):

E(\varphi ,m)={\mathcal {E}}(F(\varphi ,m),m).

The Jacobi epsilon function is not an elliptic function. However, unlike the Jacobi amplitude and coamplitude, the Jacobi epsilon function is meromorphic in the whole complex plane (in both $u$ and $m$ ).

The Jacobi zn function is defined by

\operatorname {zn} (u,m)=\int _{0}^{u}\left(\operatorname {dn} (t,m)^{2}-{\frac {E(m)}{K(m)}}\right)\,\mathrm {d} t.

It is a singly periodic function which is meromorphic in $u$ . Its minimal period is $2K(m)$ . It is related to the Jacobi zeta function by $Z(\varphi ,m)=\operatorname {zn} (F(\varphi ,m),m).$

Note that when $\varphi =\pi /2$ , that $u$ then equals the quarter period $K$ .

Definition as trigonometry: the Jacobi ellipse

Plot of the Jacobi ellipse (x² + y²/b² = 1, b real) and the twelve Jacobi elliptic functions pq(u,m) for particular values of angle φ and parameter b. The solid curve is the ellipse, with m = 1 − 1/b² and u = F(φ,m) where F(·,·) is the elliptic integral of the first kind (with parameter

m=k^{2}

). The dotted curve is the unit circle. Tangent lines from the circle and ellipse at x = cd crossing the x-axis at dc are shown in light grey.

$\cos \varphi ,\sin \varphi$ are defined on the unit circle, with radius r = 1 and angle $\varphi =$ arc length of the unit circle measured from the positive x-axis. Similarly, Jacobi elliptic functions are defined on the unit ellipse, with a = 1. Let

{\begin{aligned}&x^{2}+{\frac {y^{2}}{b^{2}}}=1,\quad b>1,\\&m=1-{\frac {1}{b^{2}}},\quad 0<m<1,\\&x=r\cos \varphi ,\quad y=r\sin \varphi \end{aligned}}

then:

r(\varphi ,m)={\frac {1}{\sqrt {1-m\sin ^{2}\varphi }}}\,.

For each angle $\varphi$ the parameter

u=u(\varphi ,m)=\int _{0}^{\varphi }r(\theta ,m)\,d\theta

(the incomplete elliptic integral of the first kind) is computed. On the unit circle ( $a=b=1$ ), $u$ would be an arc length. The quantity $u[\varphi ,k]=u(\varphi ,k^{2})$ is related to the incomplete elliptic integral of the second kind (with modulus $k$ ) by^[8]

u[\varphi ,k]={\frac {1}{\sqrt {1-k^{2}}}}\left({\frac {1+{\sqrt {1-k^{2}}}}{2}}\operatorname {E} \left(\varphi +\arctan \left({\sqrt {1-k^{2}}}\tan \varphi \right),{\frac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right)-\operatorname {E} (\varphi ,k)+{\frac {k^{2}\sin \varphi \cos \varphi }{2{\sqrt {1-k^{2}\sin ^{2}\varphi }}}}\right),

and therefore is related to the arc length of an ellipse. Let $P=(x,y)=(r\cos \varphi ,r\sin \varphi )$ be a point on the ellipse, and let $P'=(x',y')=(\cos \varphi ,\sin \varphi )$ be the point where the unit circle intersects the line between $P$ and the origin $O$ . Then the familiar relations from the unit circle:

x'=\cos \varphi ,\quad y'=\sin \varphi

read for the ellipse:

x'=\operatorname {cn} (u,m),\quad y'=\operatorname {sn} (u,m).

So the projections of the intersection point $P'$ of the line $OP$ with the unit circle on the x- and y-axes are simply $\operatorname {cn} (u,m)$ and $\operatorname {sn} (u,m)$ . These projections may be interpreted as 'definition as trigonometry'. In short:

\operatorname {cn} (u,m)={\frac {x}{r(\varphi ,m)}},\quad \operatorname {sn} (u,m)={\frac {y}{r(\varphi ,m)}},\quad \operatorname {dn} (u,m)={\frac {1}{r(\varphi ,m)}}.

For the $x$ and $y$ value of the point $P$ with $u$ and parameter $m$ we get, after inserting the relation:

r(\varphi ,m)={\frac {1}{\operatorname {dn} (u,m)}}

into: $x=r(\varphi ,m)\cos(\varphi ),y=r(\varphi ,m)\sin(\varphi )$ that:

x={\frac {\operatorname {cn} (u,m)}{\operatorname {dn} (u,m)}},\quad y={\frac {\operatorname {sn} (u,m)}{\operatorname {dn} (u,m)}}.

The latter relations for the x- and y-coordinates of points on the unit ellipse may be considered as generalization of the relations $x=\cos \varphi ,y=\sin \varphi$ for the coordinates of points on the unit circle.

The following table summarizes the expressions for all Jacobi elliptic functions pq(u,m) in the variables (x,y,r) and (φ,dn) with ${\textstyle r={\sqrt {x^{2}+y^{2}}}}$

Jacobi elliptic functions pq[u,m] as functions of {x,y,r} and {φ,dn}
		q
		c	s	n	d
p
	c	1	$x/y=\cot \varphi$	$x/r=\cos \varphi$	$x=\cos \varphi /\operatorname {dn}$
	s	$y/x=\tan \varphi$	1	$y/r=\sin \varphi$	$y=\sin \varphi /\operatorname {dn}$
	n	$r/x=\sec \varphi$	$r/y=\csc \varphi$	1	$r=1/\operatorname {dn}$
	d	$1/x=\sec \varphi \,\operatorname {dn}$	$1/y=\csc \varphi \,\operatorname {dn}$	$1/r=\operatorname {dn}$	1

Definition in terms of Jacobi theta functions

Jacobi theta function description

Equivalently, Jacobi's elliptic functions can be defined in terms of his theta functions. If we abbreviate $\vartheta _{00}(0;q)$ as $\vartheta _{00}(q)$ , and $\vartheta _{01}(0;q),\vartheta _{10}(0;q),\vartheta _{11}(0;q)$ respectively as $\vartheta _{01}(q),\vartheta _{10}(q),\vartheta _{11}(q)$ (the theta constants) then the theta function elliptic modulus k is $k={\biggl \{}{\vartheta _{10}[q(k)] \over \vartheta _{00}[q(k)]}{\biggr \}}^{2}$ . We define the nome as $q=\exp(\pi i\tau )$ in relation to the period ratio. We have

{\begin{aligned}\operatorname {sn} (u;k)&=-{\frac {\vartheta _{00}[q(k)]\,\vartheta _{11}[u\div {\bar {K}}(k);\,q(k)]}{\vartheta _{10}[q(k)]\,\vartheta _{01}[u\div {\bar {K}}(k);\,q(k)]}}\\[7pt]\operatorname {cn} (u;k)&={\frac {\vartheta _{01}[q(k)]\,\vartheta _{10}[u\div {\bar {K}}(k);\,q(k)]}{\vartheta _{10}[q(k)]\,\vartheta _{01}[u\div {\bar {K}}(k);\,q(k)]}}\\[7pt]\operatorname {dn} (u;k)&={\frac {\vartheta _{01}[q(k)]\,\vartheta _{00}[u\div {\bar {K}}(k);\,q(k)]}{\vartheta _{00}[q(k)]\,\vartheta _{01}[u\div {\bar {K}}(k);\,q(k)]}}\end{aligned}}

where ${\bar {K}}(k)={\frac {2}{\pi }}\,K(k)$ and $q=\exp[-\pi \,K'(k)/K(k)]$ .

Edmund Whittaker and George Watson defined the Jacobi theta functions this way in their textbook A Course of Modern Analysis:^[9]

\vartheta _{00}(v;w)=\prod _{n=1}^{\infty }(1-w^{2n})[1+2\cos(2v)w^{2n-1}+w^{4n-2}]

\vartheta _{01}(v;w)=\prod _{n=1}^{\infty }(1-w^{2n})[1-2\cos(2v)w^{2n-1}+w^{4n-2}]

\vartheta _{10}(v;w)=2w^{1/4}\cos v\prod _{n=1}^{\infty }(1-w^{2n})[1+2\cos(2v)w^{2n}+w^{4n}]

\vartheta _{11}(v;w)=-2w^{1/4}\sin v\prod _{n=1}^{\infty }(1-w^{2n})[1-2\cos(2v)w^{2n}+w^{4n}]

Jacobi zn function

The Jacobi zn function can be expressed by theta functions as well:

{\begin{aligned}\operatorname {zn} (u;k)&={\frac {\pi }{2K}}{\frac {\vartheta _{01}'[u\div {\bar {K}}(k);\,q(k)]}{\vartheta _{01}[u\div {\bar {K}}(k);\,q(k)]}}\\&={\frac {\pi }{2K}}{\frac {\vartheta _{00}'[u\div {\bar {K}}(k);\,q(k)]}{\vartheta _{00}[u\div {\bar {K}}(k);\,q(k)]}}+k^{2}{\frac {\operatorname {sn} (u;k)\operatorname {cn} (u;k)}{\operatorname {dn} (u;k)}}\\[6pt]&={\frac {\pi }{2K}}{\frac {\vartheta _{10}'[u\div {\bar {K}}(k);\,q(k)]}{\vartheta _{10}[u\div {\bar {K}}(k);\,q(k)]}}+{\frac {\operatorname {dn} (u;k)\operatorname {sn} (u;k)}{\operatorname {cn} (u;k)}}\\[6pt]&={\frac {\pi }{2K}}{\frac {\vartheta _{11}'[u\div {\bar {K}}(k);\,q(k)]}{\vartheta _{11}[u\div {\bar {K}}(k);\,q(k)]}}-{\frac {\operatorname {cn} (u;k)\operatorname {dn} (u;k)}{\operatorname {sn} (u;k)}}\end{aligned}}

where $'$ denotes the partial derivative with respect to the left bracket entry:

{\begin{aligned}&\vartheta '_{00}(v;w)={\frac {\partial }{\partial v}}\vartheta _{00}(v;w)\\[6pt]&\vartheta '_{01}(v;w)={\frac {\partial }{\partial v}}\vartheta _{01}(v;w)\end{aligned}}

and so on.

The following definition of the Jacobi zn function is identical to the now mentioned formulas:

{\text{zn}}(u;k)=\sum _{n=1}^{\infty }{\frac {2\pi K(k)^{-1}\sin[\pi K(k)^{-1}u]q(k)^{2n-1}}{1-2\cos[\pi K(k)^{-1}u]q(k)^{2n-1}+q(k)^{4n-2}}}

In a successive way the amplitude sine sn can be generated as follows:

\operatorname {sn} (u;k)={\frac {2{\bigl \{}{\operatorname {zn} }{\bigl (}{\tfrac {1}{2}}u;k{\bigr )}+{\operatorname {zn} }{\bigl [}K(k)-{\tfrac {1}{2}}u;k{\bigr ]}{\bigr \}}}{k^{2}+{\bigl \{}{\operatorname {zn} }{\bigl (}{\tfrac {1}{2}}u;k{\bigr )}+{\operatorname {zn} }{\bigl [}K(k)-{\tfrac {1}{2}}u;k{\bigr ]}{\bigr \}}^{2}}}

Comparison between sums and products

The reduced elliptic integral of first kind shall be defined as follows again:

{\bar {K}}(\varepsilon )={\frac {2}{\pi }}K(\varepsilon )

And the reduced elliptic nome shall be defined after this pattern:

{\bar {q}}(\varepsilon )={\sqrt[{4}]{\varepsilon ^{-2}q(\varepsilon )}}

The brothers Peter and Jonathan Borwein also gave these two following formulas for the amplitude sine in their work π and the AGM on page 60 ff:

$\operatorname {sn} (u;k)=\,{\frac {4}{{\bar {K}}(k)}}\,{\bar {q}}(k)^{2}\sin[u\div {\bar {K}}(k)]\sum _{n=1}^{\infty }{\frac {q(k)^{n-1}[1+q(k)^{2n-1}]}{1-2q(k)^{2n-1}\cos[2u\div {\bar {K}}(k)]+q(k)^{4n-2}}}$
$\operatorname {sn} (u;k)=2\,{\bar {q}}(k)\sin[u\div {\bar {K}}(k)]\prod _{n=1}^{\infty }{\frac {1-2q(k)^{2n}\cos[2u\div {\bar {K}}(k)]+q(k)^{4n}}{1-2q(k)^{2n-1}\cos[2u\div {\bar {K}}(k)]+q(k)^{4n-2}}}$

This defining formula, which results directly from the inner substitution $z\rightarrow K(k)-z$ , applies analogously to the cd function:

$\operatorname {cd} (u;k)=\,{\frac {4}{{\bar {K}}(k)}}\,{\bar {q}}(k)^{2}\cos[u\div {\bar {K}}(k)]\sum _{n=1}^{\infty }{\frac {q(k)^{n-1}[1+q(k)^{2n-1}]}{1+2q(k)^{2n-1}\cos[2u\div {\bar {K}}(k)]+q(k)^{4n-2}}}$
$\operatorname {cd} (u;k)=2\,{\bar {q}}(k)\cos[u\div {\bar {K}}(k)]\prod _{n=1}^{\infty }{\frac {1+2q(k)^{2n}\cos[2u\div {\bar {K}}(k)]+q(k)^{4n}}{1+2q(k)^{2n-1}\cos[2u\div {\bar {K}}(k)]+q(k)^{4n-2}}}$

These formulas are based on Whittaker and Watson's definition of theta non-zero value functions.

These formulas^[10] apply to the cosine amplitude:

$\operatorname {cn} (u;k)=\,{\frac {4}{{\bar {K}}(k)}}\,{\bar {q}}(k)^{2}\cos[u\div {\bar {K}}(k)]\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}q(k)^{n-1}[1-q(k)^{2n-1}]}{1-2q(k)^{2n-1}\cos[2u\div {\bar {K}}(k)]+q(k)^{4n-2}}}$
$\operatorname {cn} (u;k)=2\,{\sqrt[{4}]{1-k^{2}}}\,{\bar {q}}(k)\cos[u\div {\bar {K}}(k)]\prod _{n=1}^{\infty }{\frac {1+2q(k)^{2n}\cos[2u\div {\bar {K}}(k)]+q(k)^{4n}}{1-2q(k)^{2n-1}\cos[2u\div {\bar {K}}(k)]+q(k)^{4n-2}}}$

According to the Whittaker-Watson product formulas, this formula also applies to the delta amplitude function:

\operatorname {dn} (u;k)={\sqrt[{4}]{1-k^{2}}}\prod _{n=1}^{\infty }{\frac {1+2\cos[2u\div {\bar {K}}(k)]q(k)^{2n-1}+q(k)^{4n-2}}{1-2\cos[2u\div {\bar {K}}(k)]q(k)^{2n-1}+q(k)^{4n-2}}}

With a Hyperbolic secant sum is a definition^[11] possible for the Delta Amplitudinis:

\operatorname {dn} (z;k)={\frac {\pi }{2K{\bigl (}{\sqrt {1-k^{2}}}{\bigr )}}}\sum _{n=-\infty }^{\infty }\operatorname {sech} {\bigl \{}\pi K{\bigl (}{\sqrt {1-k^{2}}}{\bigr )}^{-1}{\bigl [}K(k)n+{\tfrac {1}{2}}z{\bigr ]}{\bigr \}}

The elliptic nome and its series

Elliptic integral and elliptic nome

Since the Jacobi functions are defined in terms of the elliptic modulus $k(\tau )$ , we need to invert this and find $\tau$ in terms of $k$ . We start from $k'={\sqrt {1-k^{2}}}$ , the complementary modulus. As a function of $\tau$ it is

k'(\tau )={\sqrt {1-k^{2}}}={\biggl \{}{\vartheta _{01}[q(k)] \over \vartheta _{00}[q(k)]}{\biggr \}}^{2}

Let us define the elliptic nome and the complete elliptic integral of the first kind:

q(k)=\exp {\biggl [}-\pi {\frac {K{\bigl (}{\sqrt {1-k^{2}}}{\bigr )}}{K(k)}}{\biggr ]}

These are two identical definitions of the complete elliptic integral of the first kind:

K(k)=\int _{0}^{\pi /2}{\frac {1}{\sqrt {1-k^{2}\sin(\varphi )^{2}}}}\partial \varphi

K(k)={\frac {\pi }{2}}\sum _{a=0}^{\infty }{\frac {[(2a)!]^{2}}{16^{a}(a!)^{4}}}k^{2a}

An identical definition of the nome function can me produced by using a series. Following function has this identity:

{\frac {1-{\sqrt[{4}]{1-k^{2}}}}{1+{\sqrt[{4}]{1-k^{2}}}}}={\frac {\vartheta _{00}[q(k)]-\vartheta _{01}[q(k)]}{\vartheta _{00}[q(k)]+\vartheta _{01}[q(k)]}}={\biggl [}\sum _{n=1}^{\infty }2\,q(k)^{(2n-1)^{2}}{\biggr ]}{\biggl [}1+\sum _{n=1}^{\infty }2\,q(k)^{4n^{2}}{\biggr ]}^{-1}

Since we may reduce to the case where the imaginary part of $\tau$ is greater than or equal to ${\sqrt {3}}/2$ (see Modular group), we can assume the absolute value of $q$ is less than or equal to $\exp(-\pi {\sqrt {3}}/2)\approx 0.0658$ ; for values this small the above series converges very rapidly and easily allows us to find the appropriate value for $q$ . By solving this function after q we get this^[12]^[13]^[14] result:

q(k)=\sum _{n=1}^{\infty }{\frac {{\text{Sc}}(n)}{2^{4n-3}}}{\biggl (}{\frac {1-{\sqrt[{4}]{1-k^{2}}}}{1+{\sqrt[{4}]{1-k^{2}}}}}{\biggr )}^{4n-3}=k^{2}{\biggl \{}{\frac {1}{2}}+{\biggl [}\sum _{n=1}^{\infty }{\frac {{\text{Sc}}(n+1)}{2^{4n+1}}}k^{2n}{\biggr ]}{\biggr \}}^{4}

This table shows numbers of the Schwarz integer sequence A002103 accurately:

Sc(1)	Sc(2)	Sc(3)	Sc(4)	Sc(5)	Sc(6)	Sc(7)	Sc(8)
1	2	15	150	1707	20910	268616	3567400

Kneser integer sequence

The German mathematician Adolf Kneser researched on the integer sequence of the elliptic period ratio in his essay Neue Untersuchung einer Reihe aus der Theorie der elliptischen Funktionen and showed that the generating function of this sequence is an elliptic function. Also a further mathematician with the name Robert Fricke analyzed this integer sequence in his essay Die elliptischen Funktionen und ihre Anwendungen and described the accurate computing methods by using this mentioned sequence. The Kneser integer sequence Kn(n) can be constructed in this way:

${\text{Kn}}(2n)=2^{4n-3}{\binom {4n}{2n}}+\sum _{m=1}^{n}4^{2n-2m}{\binom {4n}{2n-2m}}{\text{Kn}}(m)$
${\text{Kn}}(2n+1)=2^{4n-1}{\binom {4n+2}{2n+1}}+\sum _{m=1}^{n}4^{2n-2m+1}{\binom {4n+2}{2n-2m+1}}{\text{Kn}}(m)$

Executed examples:

${\text{Kn}}(2)=2\times 6+1\times {\color {cornflowerblue}1}={\color {cornflowerblue}13}$
${\text{Kn}}(3)=8\times 20+24\times {\color {cornflowerblue}1}={\color {cornflowerblue}184}$
${\text{Kn}}(4)=32\times 70+448\times {\color {cornflowerblue}1}+1\times {\color {cornflowerblue}13}={\color {cornflowerblue}2701}$
${\text{Kn}}(5)=128\times 252+7680\times {\color {cornflowerblue}1}+40\times {\color {cornflowerblue}13}={\color {cornflowerblue}40456}$
${\text{Kn}}(6)=512\times 924+126720\times {\color {cornflowerblue}1}+1056\times {\color {cornflowerblue}13}+1\times {\color {cornflowerblue}184}={\color {cornflowerblue}613720}$
${\text{Kn}}(7)=2048\times 3432+2050048\times {\color {cornflowerblue}1}+23296\times {\color {cornflowerblue}13}+56\times {\color {cornflowerblue}184}={\color {cornflowerblue}9391936}$

The Kneser sequence appears in the Taylor series of the period ratio (half period ratio):

{\frac {1}{4}}\ln \left({\frac {16}{x^{2}}}\right)-{\frac {\pi \,K'(x)}{4\,K(x)}}=\sum _{n=1}^{\infty }{\frac {{\text{Kn}}(n)}{2^{4n-1}n}}\,x^{2n}

Schellbach Schwarz integer sequence

The mathematician Karl Heinrich Schellbach discovered the integer number sequence that appears in the MacLaurin series of the Elliptic Nome function. This scientist^[15] constructed this sequence A002103 in his work Die Lehre von den elliptischen Integralen und den Thetafunktionen in detail. Especially on page 60 of this work a synthesis route of this sequence is written down in his work. Also the Silesian German mathematician Hermann Amandus Schwarz wrote in his work Formeln und Lehrsätze zum Gebrauche der elliptischen Funktionen in the chapter Berechnung der Grösse k on pages 54 to 56 that integer number sequence down. This Schellbach Schwarz number sequence Sc(n) (OEIS: A002103) was also analyzed by the mathematicians Karl Theodor Wilhelm Weierstrass and Louis Melville Milne-Thomson in the 20th century. The mathematician Adolf Kneser determined a synthesis method for this sequence based on the following pattern:

{\text{Sc}}(n+1)={\frac {2}{n}}\sum _{m=1}^{n}{\text{Sc}}(m){\text{Kn}}(n+1-m)

The Schellbach Schwarz sequence Sc(n) is entered in the online encyclopedia of number sequences under the number A002103 and the Kneser sequence Kn(n) is entered under the number A227503. Adolf Kneser researched on this integer sequence in his essay Neue Untersuchung einer Reihe aus der Theorie der elliptischen Funktionen and showed that the generating function of this sequence is an elliptic function. Also Robert Fricke analyzed this integer sequence in his essay Die elliptischen Funktionen und ihre Anwendungen and described accurate computing methods by using this sequence. Following table^[16]^[17] contains the Kneser numbers and the Schellbach Schwarz numbers:

Constructed sequences Kneser and Schellbach Schwarz
Index n	Kn(n) (A227503)	Sc(n) (A002103)
1	1	1
2	13	2
3	184	15
4	2701	150
5	40456	1707
6	613720	20910
7	9391936	268616
8	144644749	3567400

In the following, it will be shown as an example how the Schellbach Schwarz numbers are built up successively. For this, the examples with the numbers Sc(4) = 150, Sc(5) = 1707 and Sc(6) = 20910 are used:

\mathrm {Sc} (4)={\tfrac {2}{3}}\sum _{m=1}^{3}\mathrm {Sc} (m)\,\mathrm {Kn} (4-m)={\tfrac {2}{3}}{\bigl [}{\color {navy}\mathrm {Sc} (1)}\,{\color {cornflowerblue}\mathrm {Kn} (3)}+{\color {navy}\mathrm {Sc} (2)}\,{\color {cornflowerblue}\mathrm {Kn} (2)}+{\color {navy}\mathrm {Sc} (3)}\,{\color {cornflowerblue}\mathrm {Kn} (1)}{\bigr ]}

{\color {navy}\mathrm {Sc} (4)}={\tfrac {2}{3}}{\bigl (}{\color {navy}1}\times {\color {cornflowerblue}184}+{\color {navy}2}\times {\color {cornflowerblue}13}+{\color {navy}15}\times {\color {cornflowerblue}1}{\bigr )}={\color {navy}150}

\mathrm {Sc} (5)={\tfrac {2}{4}}\sum _{m=1}^{4}\mathrm {Sc} (m)\,\mathrm {Kn} (5-m)={\tfrac {2}{4}}{\bigl [}{\color {navy}\mathrm {Sc} (1)}\,{\color {cornflowerblue}\mathrm {Kn} (4)}+{\color {navy}\mathrm {Sc} (2)}\,{\color {cornflowerblue}\mathrm {Kn} (3)}+{\color {navy}\mathrm {Sc} (3)}\,{\color {cornflowerblue}\mathrm {Kn} (2)}+{\color {navy}\mathrm {Sc} (4)}\,{\color {cornflowerblue}\mathrm {Kn} (1)}{\bigr ]}

{\color {navy}\mathrm {Sc} (5)}={\tfrac {2}{4}}{\bigl (}{\color {navy}1}\times {\color {cornflowerblue}2701}+{\color {navy}2}\times {\color {cornflowerblue}184}+{\color {navy}15}\times {\color {cornflowerblue}13}+{\color {navy}150}\times {\color {cornflowerblue}1}{\bigr )}={\color {navy}1707}

\mathrm {Sc} (6)={\tfrac {2}{5}}\sum _{m=1}^{5}\mathrm {Sc} (m)\,\mathrm {Kn} (6-m)={\tfrac {2}{5}}{\bigl [}{\color {navy}\mathrm {Sc} (1)}\,{\color {cornflowerblue}\mathrm {Kn} (5)}+{\color {navy}\mathrm {Sc} (2)}\,{\color {cornflowerblue}\mathrm {Kn} (4)}+{\color {navy}\mathrm {Sc} (3)}\,{\color {cornflowerblue}\mathrm {Kn} (3)}+{\color {navy}\mathrm {Sc} (4)}\,{\color {cornflowerblue}\mathrm {Kn} (2)}+{\color {navy}\mathrm {Sc} (5)}\,{\color {cornflowerblue}\mathrm {Kn} (1)}{\bigr ]}

{\color {navy}\mathrm {Sc} (6)}={\tfrac {2}{5}}{\bigl (}{\color {navy}1}\times {\color {cornflowerblue}40456}+{\color {navy}2}\times {\color {cornflowerblue}2701}+{\color {navy}15}\times {\color {cornflowerblue}184}+{\color {navy}150}\times {\color {cornflowerblue}13}+{\color {navy}1707}\times {\color {cornflowerblue}1}{\bigr )}={\color {navy}20910}

And this sequence creates the MacLaurin series of the elliptic nome in exactly this way mentioned above:

q(x)=\sum _{n=1}^{\infty }{\frac {{\text{Sc}}(n)}{2^{4n-3}}}{\biggl (}{\frac {1-{\sqrt[{4}]{1-x^{2}}}}{1+{\sqrt[{4}]{1-x^{2}}}}}{\biggr )}^{4n-3}=x^{2}{\biggl \{}{\frac {1}{2}}+{\biggl [}\sum _{n=1}^{\infty }{\frac {{\text{Sc}}(n+1)}{2^{4n+1}}}x^{2n}{\biggr ]}{\biggr \}}^{4}

Definition in terms of Neville theta functions

The Jacobi elliptic functions can be defined very simply using the Neville theta functions:^[18]

\operatorname {pq} (u,m)={\frac {\theta _{\operatorname {p} }(u,m)}{\theta _{\operatorname {q} }(u,m)}}

Simplifications of complicated products of the Jacobi elliptic functions are often made easier using these identities.

Jacobi transformations

The Jacobi imaginary transformations

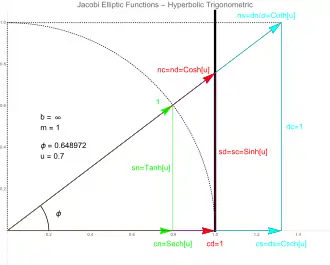
Plot of the degenerate Jacobi curve (x² + y²/b² = 1, b = ∞) and the twelve Jacobi Elliptic functions pq(u,1) for a particular value of angle φ. The solid curve is the degenerate ellipse (x² = 1) with m = 1 and u = F(φ,1) where F(·,·) is the elliptic integral of the first kind. The dotted curve is the unit circle. Since these are the Jacobi functions for m = 0 (circular trigonometric functions) but with imaginary arguments, they correspond to the six hyperbolic trigonometric functions.

The Jacobi imaginary transformations relate various functions of the imaginary variable i u or, equivalently, relations between various values of the m parameter. In terms of the major functions:^[19]^: 506

\operatorname {cn} (u,m)=\operatorname {nc} (i\,u,1\!-\!m)

\operatorname {sn} (u,m)=-i\operatorname {sc} (i\,u,1\!-\!m)

\operatorname {dn} (u,m)=\operatorname {dc} (i\,u,1\!-\!m)

Using the multiplication rule, all other functions may be expressed in terms of the above three. The transformations may be generally written as $\operatorname {pq} (u,m)=\gamma _{\operatorname {pq} }\operatorname {pq} '(i\,u,1\!-\!m)$ . The following table gives the $\gamma _{\operatorname {pq} }\operatorname {pq} '(i\,u,1\!-\!m)$ for the specified pq(u,m).^[18] (The arguments $(i\,u,1\!-\!m)$ are suppressed)

Jacobi Imaginary transformations $\gamma _{\operatorname {pq} }\operatorname {pq} '(i\,u,1\!-\!m)$
		q
		c	s	n	d
p
	c	1	i ns	nc	nd
	s	−i sn	1	−i sc	−i sd
	n	cn	i cs	1	cd
	d	dn	i ds	dc	1

Since the hyperbolic trigonometric functions are proportional to the circular trigonometric functions with imaginary arguments, it follows that the Jacobi functions will yield the hyperbolic functions for m=1.^[5]^: 249 In the figure, the Jacobi curve has degenerated to two vertical lines at x = 1 and x = −1.

The Jacobi real transformations

The Jacobi real transformations^[5]^: 308 yield expressions for the elliptic functions in terms with alternate values of m. The transformations may be generally written as $\operatorname {pq} (u,m)=\gamma _{\operatorname {pq} }\operatorname {pq} '(k\,u,1/m)$ . The following table gives the $\gamma _{\operatorname {pq} }\operatorname {pq} '(k\,u,1/m)$ for the specified pq(u,m).^[18] (The arguments $(k\,u,1/m)$ are suppressed)

Jacobi real transformations $\gamma _{\operatorname {pq} }\operatorname {pq} '(k\,u,1/m)$
		q
		c	s	n	d
p
	c	$1$	$k\operatorname {ds}$	$\operatorname {dn}$	$\operatorname {dc}$
	s	${\frac {1}{k}}\operatorname {sd}$	$1$	${\frac {1}{k}}\operatorname {sn}$	${\frac {1}{k}}\operatorname {sc}$
	n	$\operatorname {nd}$	$k\operatorname {ns}$	$1$	$\operatorname {nc}$
	d	$\operatorname {cd}$	$k\operatorname {cs}$	$\operatorname {cn}$	$1$

Other Jacobi transformations

Jacobi's real and imaginary transformations can be combined in various ways to yield three more simple transformations .^[5]^: 214 The real and imaginary transformations are two transformations in a group (D₃ or anharmonic group) of six transformations. If

\mu _{R}(m)=1/m

is the transformation for the m parameter in the real transformation, and

\mu _{I}(m)=1-m=m'

is the transformation of m in the imaginary transformation, then the other transformations can be built up by successive application of these two basic transformations, yielding only three more possibilities:

{\begin{aligned}\mu _{IR}(m)&=&\mu _{I}(\mu _{R}(m))&=&-m'/m\\\mu _{RI}(m)&=&\mu _{R}(\mu _{I}(m))&=&1/m'\\\mu _{RIR}(m)&=&\mu _{R}(\mu _{I}(\mu _{R}(m)))&=&-m/m'\end{aligned}}

These five transformations, along with the identity transformation (μ_U(m) = m) yield the six-element group. With regard to the Jacobi elliptic functions, the general transformation can be expressed using just three functions:

\operatorname {cs} (u,m)=\gamma _{i}\operatorname {cs'} (\gamma _{i}u,\mu _{i}(m))

\operatorname {ns} (u,m)=\gamma _{i}\operatorname {ns'} (\gamma _{i}u,\mu _{i}(m))

\operatorname {ds} (u,m)=\gamma _{i}\operatorname {ds'} (\gamma _{i}u,\mu _{i}(m))

where i = U, I, IR, R, RI, or RIR, identifying the transformation, γ_i is a multiplication factor common to these three functions, and the prime indicates the transformed function. The other nine transformed functions can be built up from the above three. The reason the cs, ns, ds functions were chosen to represent the transformation is that the other functions will be ratios of these three (except for their inverses) and the multiplication factors will cancel.

The following table lists the multiplication factors for the three ps functions, the transformed m's, and the transformed function names for each of the six transformations.^[5]^: 214 (As usual, k² = m, 1 − k² = k₁² = m′ and the arguments ( $\gamma _{i}u,\mu _{i}(m)$ ) are suppressed)

Parameters for the six transformations
Transformation i	$\gamma _{i}$	$\mu _{i}(m)$	cs'	ns'	ds'
U	1	m	cs	ns	ds
I	i	m′	ns	cs	ds
IR	i k	−m′/m	ds	cs	ns
R	k	1/m	ds	ns	cs
RI	i k₁	1/m′	ns	ds	cs
RIR	k₁	−m/m′	cs	ds	ns

Thus, for example, we may build the following table for the RIR transformation.^[18] The transformation is generally written $\operatorname {pq} (u,m)=\gamma _{\operatorname {pq} }\,\operatorname {pq'} (k'\,u,-m/m')$ (The arguments $(k'\,u,-m/m')$ are suppressed)

The RIR transformation $\gamma _{\operatorname {pq} }\,\operatorname {pq'} (k'\,u,-m/m')$
		q
		c	s	n	d
p
	c	1	k' cs	cd	cn
	s	${\frac {1}{k'}}$ sc	1	${\frac {1}{k'}}$ sd	${\frac {1}{k'}}$ sn
	n	dc	$k'$ ds	1	dn
	d	nc	$k'$ ns	nd	1

The value of the Jacobi transformations is that any set of Jacobi elliptic functions with any complex-valued parameter m can be converted into another set for which 0 ≤ m ≤ 1 and, for real values of u, the function values will be real.^[5]^{: p. 215}

The Jacobi hyperbola

Plot of the Jacobi hyperbola (x² + y²/b² = 1, b imaginary) and the twelve Jacobi Elliptic functions pq(u,m) for particular values of angle φ and parameter b. The solid curve is the hyperbola, with m = 1 − 1/b² and u = F(φ,m) where F(·,·) is the elliptic integral of the first kind. The dotted curve is the unit circle. For the ds-dc triangle, σ = sinφ cos φ.

Introducing complex numbers, our ellipse has an associated hyperbola:

x^{2}-{\frac {y^{2}}{b^{2}}}=1

from applying Jacobi's imaginary transformation^[18] to the elliptic functions in the above equation for x and y.

x={\frac {1}{\operatorname {dn} (u,1-m)}},\quad y={\frac {\operatorname {sn} (u,1-m)}{\operatorname {dn} (u,1-m)}}

It follows that we can put $x=\operatorname {dn} (u,1-m),y=\operatorname {sn} (u,1-m)$ . So our ellipse has a dual ellipse with m replaced by 1-m. This leads to the complex torus mentioned in the Introduction.^[20] Generally, m may be a complex number, but when m is real and m<0, the curve is an ellipse with major axis in the x direction. At m=0 the curve is a circle, and for 0<m<1, the curve is an ellipse with major axis in the y direction. At m = 1, the curve degenerates into two vertical lines at x = ±1. For m > 1, the curve is a hyperbola. When m is complex but not real, x or y or both are complex and the curve cannot be described on a real x-y diagram.

Minor functions

Reversing the order of the two letters of the function name results in the reciprocals of the three functions above:

\operatorname {ns} (u)={\frac {1}{\operatorname {sn} (u)}},\qquad \operatorname {nc} (u)={\frac {1}{\operatorname {cn} (u)}},\qquad \operatorname {nd} (u)={\frac {1}{\operatorname {dn} (u)}}.

Similarly, the ratios of the three primary functions correspond to the first letter of the numerator followed by the first letter of the denominator:

{\begin{aligned}\operatorname {sc} (u)={\frac {\operatorname {sn} (u)}{\operatorname {cn} (u)}},\qquad \operatorname {sd} (u)={\frac {\operatorname {sn} (u)}{\operatorname {dn} (u)}},\qquad \operatorname {dc} (u)={\frac {\operatorname {dn} (u)}{\operatorname {cn} (u)}},\qquad \operatorname {ds} (u)={\frac {\operatorname {dn} (u)}{\operatorname {sn} (u)}},\qquad \operatorname {cs} (u)={\frac {\operatorname {cn} (u)}{\operatorname {sn} (u)}},\qquad \operatorname {cd} (u)={\frac {\operatorname {cn} (u)}{\operatorname {dn} (u)}}.\end{aligned}}

More compactly, we have

\operatorname {pq} (u)={\frac {\operatorname {pn} (u)}{\operatorname {qn} (u)}}

where p and q are any of the letters s, c, d.

Periodicity, poles, and residues

Plots of the phase for the twelve Jacobi Elliptic functions pq(u,m) as a function complex argument u, with poles and zeroes indicated. The plots are over one full cycle in the real and imaginary directions with the colored portion indicating phase according to the color wheel at the lower right (which replaces the trivial dd function). Regions with absolute value below 1/3 are colored black, roughly indicating the location of a zero, while regions with absolute value above 3 are colored white, roughly indicating the position of a pole. All plots use m = 2/3 with K = K(m), K′ = K(1 − m), K(·) being the complete elliptic integral of the first kind. Arrows at the poles point in direction of zero phase. Right and left arrows imply positive and negative real residues respectively. Up and down arrows imply positive and negative imaginary residues respectively.

In the complex plane of the argument u, the Jacobi elliptic functions form a repeating pattern of poles (and zeroes). The residues of the poles all have the same absolute value, differing only in sign. Each function pq(u,m) has an "inverse function" (in the multiplicative sense) qp(u,m) in which the positions of the poles and zeroes are exchanged. The periods of repetition are generally different in the real and imaginary directions, hence the use of the term "doubly periodic" to describe them.

The Jacobi amplitude and the Jacobi epsilon function are quasi-periodic:

\operatorname {am} (u+2K,m)=\operatorname {am} (u,m)+\pi ,

{\mathcal {E}}(u+2K,m)={\mathcal {E}}(u,m)+2E

where $E(m)$ is the complete elliptic integral of the second kind with parameter $m$ .

Also

\operatorname {zn} (u+2iK',m)=\operatorname {zn} (u,m)-{\frac {\pi i}{K}}

.

The double periodicity of the Jacobi elliptic functions may be expressed as:

\operatorname {pq} (u+2\alpha K(m)+2i\beta K(1-m)\,,\,m)=(-1)^{\gamma }\operatorname {pq} (u,m)

where α and β are any pair of integers. K(·) is the complete elliptic integral of the first kind, also known as the quarter period. The power of negative unity (γ) is given in the following table:

$\gamma$
		q
		c	s	n	d
p
	c	0	β	α + β	α
	s	β	0	α	α + β
	n	α + β	α	0	β
	d	α	α + β	β	0

When the factor (−1)^γ is equal to −1, the equation expresses quasi-periodicity. When it is equal to unity, it expresses full periodicity. It can be seen, for example, that for the entries containing only α when α is even, full periodicity is expressed by the above equation, and the function has full periods of 4K(m) and 2iK(1 − m). Likewise, functions with entries containing only β have full periods of 2K(m) and 4iK(1 − m), while those with α + β have full periods of 4K(m) and 4iK(1 − m).

In the diagram on the right, which plots one repeating unit for each function, indicating phase along with the location of poles and zeroes, a number of regularities can be noted: The inverse of each function is opposite the diagonal, and has the same size unit cell, with poles and zeroes exchanged. The pole and zero arrangement in the auxiliary rectangle formed by (0,0), (K,0), (0,K′) and (K,K′) are in accordance with the description of the pole and zero placement described in the introduction above. Also, the size of the white ovals indicating poles are a rough measure of the absolute value of the residue for that pole. The residues of the poles closest to the origin in the figure (i.e. in the auxiliary rectangle) are listed in the following table:

Residues of Jacobi elliptic functions
		q
		c	s	n	d
p
	c		1	$-{\frac {i}{k}}$	$-{\frac {1}{k}}$
	s	$-{\frac {1}{k'}}$		${\frac {1}{k}}$	$-{\frac {i}{k\,k'}}$
	n	$-{\frac {1}{k'}}$	1		$-{\frac {i}{k'}}$
	d	-1	1	$-i$

When applicable, poles displaced above by 2K or displaced to the right by 2K′ have the same value but with signs reversed, while those diagonally opposite have the same value. Note that poles and zeroes on the left and lower edges are considered part of the unit cell, while those on the upper and right edges are not.

Special values

Lemniscatic values

The Values along with the modulus $k={\tfrac {1}{2}}{\sqrt {2}}=\lambda ^{*}(1)$ are called lemniscatic values:

Values for the thirds of the integral K:

\operatorname {sn} {\bigl [}{\tfrac {1}{3}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}({\sqrt[{4}]{12}}-{\sqrt {3}}+1)

\operatorname {cn} {\bigl [}{\tfrac {2}{3}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}({\sqrt {3}}-{\sqrt[{4}]{12}}+1)

\operatorname {cn} {\bigl [}{\tfrac {1}{3}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\sqrt[{4}]{2{\sqrt {3}}-3}}

\operatorname {sn} {\bigl [}{\tfrac {2}{3}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}({\sqrt[{4}]{27}}+{\sqrt[{4}]{3}}-{\sqrt {2}}){\sqrt[{4}]{2{\sqrt {3}}-3}}

Values for the fifths of the integral K:

\operatorname {sn} {\bigl [}{\tfrac {1}{5}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}{\Bigl (}{\tan {\tfrac {1}{5}}\pi }+1-{\sqrt {2\tan {\tfrac {3}{20}}\pi }}\,{\Bigr )}

\operatorname {sn} {\bigl [}{\tfrac {3}{5}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}{\Bigl (}{\tan {\tfrac {1}{5}}\pi }-1+{\sqrt {2\cot {\tfrac {3}{20}}\pi }}\,{\Bigr )}

\operatorname {cn} {\bigl [}{\tfrac {2}{5}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}{\Bigl (}{\cot {\tfrac {1}{10}}\pi }-1-{\sqrt {2\tan {\tfrac {1}{20}}\pi }}\,{\Bigr )}

\operatorname {cn} {\bigl [}{\tfrac {4}{5}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}{\Bigl (}{\cot {\tfrac {1}{10}}\pi }+1-{\sqrt {2\cot {\tfrac {1}{20}}\pi }}\,{\Bigr )}

For the corresponding Pythagorean opposites these formulas are valid:

\operatorname {cn} {\bigl [}{\tfrac {1}{5}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}=2{\sqrt[{4}]{{\sqrt {5}}-2}}\,{\sqrt {\sin {\tfrac {3}{20}}\pi \,\cos {\tfrac {1}{20}}\pi }}

\operatorname {cn} {\bigl [}{\tfrac {3}{5}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}=2{\sqrt[{4}]{{\sqrt {5}}-2}}\,{\sqrt {\sin {\tfrac {1}{20}}\pi \,\cos {\tfrac {3}{20}}\pi }}

\operatorname {sn} {\bigl [}{\tfrac {2}{5}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}{\sqrt[{4}]{2\tan {\tfrac {1}{20}}\pi }}\,\left({\sqrt {\cot {\tfrac {1}{10}}\pi +1}}-{\sqrt {\cot {\tfrac {1}{10}}\pi -3}}\,\right)

\operatorname {sn} {\bigl [}{\tfrac {4}{5}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}{\sqrt[{4}]{2\cot {\tfrac {1}{20}}\pi }}\,\left({\sqrt {\cot {\tfrac {1}{10}}\pi +3}}-{\sqrt {\cot {\tfrac {1}{10}}\pi -1}}\,\right)

Values for the sevenths of the integral K:

\operatorname {cn} {\bigl [}{\tfrac {2}{7}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}=\tanh {\Bigl [}{\tfrac {1}{2}}\operatorname {arcoth} {\Bigl (}{\tfrac {1}{2}}{\sqrt {2\sin {\tfrac {1}{7}}\pi \,\cot {\tfrac {3}{28}}\pi }}+\sin {\tfrac {1}{14}}\pi {\Bigr )}{\Bigr ]}

\operatorname {cn} {\bigl [}{\tfrac {4}{7}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}=\tanh {\Bigl [}{\tfrac {1}{2}}\operatorname {arcoth} {\Bigl (}{\tfrac {1}{2}}{\sqrt {2\cos {\tfrac {1}{14}}\pi \,\tan {\tfrac {5}{28}}\pi }}+\sin {\tfrac {3}{14}}\pi {\Bigr )}{\Bigr ]}

\operatorname {cn} {\bigl [}{\tfrac {6}{7}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}=\tanh {\Bigl [}{\tfrac {1}{2}}\operatorname {arcoth} {\Bigl (}{\tfrac {1}{2}}{\sqrt {2\cos {\tfrac {3}{14}}\pi \,\cot {\tfrac {1}{28}}\pi }}+\cos {\tfrac {1}{7}}\pi {\Bigr )}{\Bigr ]}

For the corresponding Pythagorean opposites these formulas are valid:

\operatorname {sn} {\bigl [}{\tfrac {2}{7}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}=\operatorname {sech} {\Bigl [}{\tfrac {1}{2}}\operatorname {arcoth} {\Bigl (}{\tfrac {1}{2}}{\sqrt {2\sin {\tfrac {1}{7}}\pi \,\cot {\tfrac {3}{28}}\pi }}+\sin {\tfrac {1}{14}}\pi {\Bigr )}{\Bigr ]}

\operatorname {sn} {\bigl [}{\tfrac {4}{7}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}=\operatorname {sech} {\Bigl [}{\tfrac {1}{2}}\operatorname {arcoth} {\Bigl (}{\tfrac {1}{2}}{\sqrt {2\cos {\tfrac {1}{14}}\pi \,\tan {\tfrac {5}{28}}\pi }}+\sin {\tfrac {3}{14}}\pi {\Bigr )}{\Bigr ]}

\operatorname {sn} {\bigl [}{\tfrac {6}{7}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}=\operatorname {sech} {\Bigl [}{\tfrac {1}{2}}\operatorname {arcoth} {\Bigl (}{\tfrac {1}{2}}{\sqrt {2\cos {\tfrac {3}{14}}\pi \,\cot {\tfrac {1}{28}}\pi }}+\cos {\tfrac {1}{7}}\pi {\Bigr )}{\Bigr ]}

Important identities:

Setting $k={\tfrac {1}{2}}{\sqrt {2}}$ gives the lemniscate elliptic functions $\operatorname {sl}$ and $\operatorname {cl}$ in this way:

\operatorname {sl} (u)={\tfrac {1}{2}}{\sqrt {2}}\,\operatorname {sd} {\bigl (}{\sqrt {2}}\,u;{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )}={\tfrac {1}{2}}{\sqrt {2}}\,{\frac {\operatorname {sn} {\bigl (}{\sqrt {2}}\,u;{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )}}{\operatorname {dn} {\bigl (}{\sqrt {2}}\,u;{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )}}},\quad \operatorname {cl} (u)=\operatorname {cn} {\bigl (}{\sqrt {2}}\,u;{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )}.

Setting $k=i$ gives the lemniscate elliptic functions $\operatorname {sl}$ and $\operatorname {cl}$ in the following way:

\operatorname {sl} (u)=\operatorname {sn} (u;i),\quad \operatorname {cl} (u)=\operatorname {cd} (u;i)={\frac {\operatorname {cn} (u;i)}{\operatorname {dn} (u;i)}}.

Equianharmonic values

The Values along with the modulus $k=\sin {\tfrac {1}{12}}\pi =\lambda ^{*}(3)$ and $k=\cos {\tfrac {1}{12}}\pi =\lambda ^{*}{\bigl (}{\tfrac {1}{3}}{\bigr )}$ are called equianharmonic values or also values of the Equianharmonic Case:

\operatorname {cn} {\bigl [}{\tfrac {2}{5}}K{\bigl (}\sin {\tfrac {1}{12}}\pi {\bigr )};\,\sin {\tfrac {1}{12}}\pi {\bigr ]}=\tan {\bigl [}\arctan {\bigl (}{\sqrt[{3}]{10}}\tan {\tfrac {1}{10}}\pi +{\tfrac {1}{3}}{\sqrt {3}}({\sqrt[{3}]{10}}-1){\bigr )}-{\tfrac {1}{12}}\pi {\bigr ]}

\operatorname {cn} {\bigl [}{\tfrac {4}{5}}K{\bigl (}\sin {\tfrac {1}{12}}\pi {\bigr )};\,\sin {\tfrac {1}{12}}\pi {\bigr ]}=\tan {\bigl [}\arctan {\bigl (}{\sqrt[{3}]{10}}\tan {\tfrac {1}{10}}\pi -{\tfrac {1}{3}}{\sqrt {3}}({\sqrt[{3}]{10}}-1){\bigr )}+{\tfrac {1}{12}}\pi {\bigr ]}

\operatorname {cn} {\bigl [}{\tfrac {2}{5}}K{\bigl (}\cos {\tfrac {1}{12}}\pi {\bigr )};\,\cos {\tfrac {1}{12}}\pi {\bigr ]}=\cot {\bigl [}\arctan {\bigl (}{\sqrt[{3}]{10}}\cot {\tfrac {1}{5}}\pi +{\tfrac {1}{3}}{\sqrt {3}}({\sqrt[{3}]{10}}-1){\bigr )}-{\tfrac {1}{12}}\pi {\bigr ]}

\operatorname {cn} {\bigl [}{\tfrac {4}{5}}K{\bigl (}\cos {\tfrac {1}{12}}\pi {\bigr )};\,\cos {\tfrac {1}{12}}\pi {\bigr ]}=\cot {\bigl [}\arctan {\bigl (}{\sqrt[{3}]{10}}\cot {\tfrac {1}{5}}\pi -{\tfrac {1}{3}}{\sqrt {3}}({\sqrt[{3}]{10}}-1){\bigr )}+{\tfrac {1}{12}}\pi {\bigr ]}

The flower marks the Elliptic lambda star function!

Elementary functions

When $k=0$ or $k=1$ , the Jacobi elliptic functions are reduced to non-elliptic functions:

Function	k = 0	k = 1
$\operatorname {sn} (u;k)$	$\sin u$	$\tanh u$
$\operatorname {cn} (u;k)$	$\cos u$	$\operatorname {sech} u$
$\operatorname {dn} (u;k)$	$1$	$\operatorname {sech} u$
$\operatorname {ns} (u;k)$	$\csc u$	$\coth u$
$\operatorname {nc} (u;k)$	$\sec u$	$\cosh u$
$\operatorname {nd} (u;k)$	$1$	$\cosh u$
$\operatorname {sd} (u;k)$	$\sin u$	$\sinh u$
$\operatorname {cd} (u;k)$	$\cos u$	$1$
$\operatorname {cs} (u;k)$	$\cot u$	$\operatorname {csch} u$
$\operatorname {ds} (u;k)$	$\csc u$	$\operatorname {csch} u$
$\operatorname {dc} (u;k)$	$\sec u$	$1$
$\operatorname {sc} (u;k)$	$\tan u$	$\sinh u$

For the Jacobi amplitude, $\operatorname {am} (u;0)=u$ and $\operatorname {am} (u;1)=\operatorname {gd} u$ where $\operatorname {gd}$ is the Gudermannian function.

In general if neither of p, q is d then $\operatorname {pq} (u;1)=\operatorname {pq} (\operatorname {gd} (u);0)$ .

Identities

Addition theorems

The functions satisfy the two square relations in dependency of the modulus $k$ in Legendre form:

\operatorname {cn} ^{2}(u;k)+\operatorname {sn} ^{2}(u;k)=1,\,

\operatorname {dn} ^{2}(u;k)+k^{2}\operatorname {sn} ^{2}(u;k)=1.\,

From this we see that (cn, sn, dn) parametrizes an elliptic curve which is the intersection of the two quadrics defined by the above two equations. We now may define a group law for points on this curve by the addition formulas for the Jacobi functions^[3]^[21]

{\begin{aligned}\operatorname {sn} (x+y;k)&={\operatorname {sn} (x;k)\operatorname {cn} (y;k)\operatorname {dn} (y;k)+\operatorname {sn} (y;k)\operatorname {cn} (x;k)\operatorname {dn} (x;k) \over {1-k^{2}\operatorname {sn} ^{2}(x;k)\operatorname {sn} ^{2}(y;k)}},\\[8pt]\operatorname {cn} (x+y;k)&={\operatorname {cn} (x;k)\operatorname {cn} (y;k)-\operatorname {sn} (x;k)\operatorname {sn} (y;k)\operatorname {dn} (x;k)\operatorname {dn} (y;k) \over {1-k^{2}\operatorname {sn} ^{2}(x;k)\operatorname {sn} ^{2}(y;k)}},\\[8pt]\operatorname {dn} (x+y;k)&={\operatorname {dn} (x;k)\operatorname {dn} (y;k)-k^{2}\operatorname {sn} (x;k)\operatorname {sn} (y;k)\operatorname {cn} (x;k)\operatorname {cn} (y;k) \over {1-k^{2}\operatorname {sn} ^{2}(x;k)\operatorname {sn} ^{2}(y;k)}}.\end{aligned}}

By only treating the functions sn and cd, the following pair of addition theorems can be established in which the two theorems are antisymmetric to each other:

${\color {blueviolet}\operatorname {sn} }(x+y;k)={\frac {{\color {blueviolet}\operatorname {sn} }(x;k)\,{\color {blue}\operatorname {cd} }(y;k)+{\color {blue}\operatorname {cd} }(x;k)\,{\color {blueviolet}\operatorname {sn} }(y;k)}{1+k^{2}\,{\color {blueviolet}\operatorname {sn} }(x;k)\,{\color {blue}\operatorname {cd} }(x;k)\,{\color {blueviolet}\operatorname {sn} }(y;k)\,{\color {blue}\operatorname {cd} }(y;k)}}$
${\color {blue}\operatorname {cd} }(x+y;k)={\frac {{\color {blue}\operatorname {cd} }(x;k)\,{\color {blue}\operatorname {cd} }(y;k)-{\color {blueviolet}\operatorname {sn} }(x;k)\,{\color {blueviolet}\operatorname {sn} }(y;k)}{1-k^{2}\,{\color {blueviolet}\operatorname {sn} }(x;k)\,{\color {blue}\operatorname {cd} }(x;k)\,{\color {blueviolet}\operatorname {sn} }(y;k)\,{\color {blue}\operatorname {cd} }(y;k)}}$

The Jacobi epsilon and zn functions satisfy a quasi-addition theorem:

{\begin{aligned}{\mathcal {E}}(x+y;k)&={\mathcal {E}}(x;k)+{\mathcal {E}}(y;k)-k^{2}\operatorname {sn} (x;k)\operatorname {sn} (y;k)\operatorname {sn} (x+y;k),\\\operatorname {zn} (x+y;k)&=\operatorname {zn} (x;k)+\operatorname {zn} (y;k)-k^{2}\operatorname {sn} (x;k)\operatorname {sn} (y;k)\operatorname {sn} (x+y;k).\end{aligned}}

Double angle formulae can be easily derived from the above equations by setting x = y.^[3] Half angle formulae^[18]^[3] are all of the form:

\operatorname {pq} {\bigl (}{\tfrac {1}{2}}u;k{\bigr )}^{2}=f_{\mathrm {p} }/f_{\mathrm {q} }

where:

f_{\mathrm {c} }=\operatorname {cn} (u;k)+\operatorname {dn} (u;k)

f_{\mathrm {s} }=1-\operatorname {cn} (u;k)

f_{\mathrm {n} }=1+\operatorname {dn} (u;k)

f_{\mathrm {d} }=(1+\operatorname {dn} (u;k))-m(1-\operatorname {cn} (u;k))

Half Angle formula

These three formulas describe the halving theorem:

\operatorname {sn} \left({\tfrac {1}{2}}u;k\right)^{2}={\frac {1-\operatorname {cn} (u;k)}{1+\operatorname {dn} (u;k)}}

\operatorname {cn} \left({\tfrac {1}{2}}u;k\right)^{2}={\frac {\operatorname {cn} (u;k)+\operatorname {dn} (u;k)}{1+\operatorname {dn} (u;k)}}

\operatorname {dn} \left({\tfrac {1}{2}}u;k\right)^{2}={\frac {1-k^{2}+\operatorname {dn} (u;k)+k^{2}\operatorname {cn} (u;k)}{1+\operatorname {dn} (u;k)}}

And the theorem of the arithmetic mean is described by this formula:

\operatorname {sn} {\bigl (}{\tfrac {1}{2}}x+{\tfrac {1}{2}}y;k{\bigr )}^{2}={\frac {1+\operatorname {sn} (x;k)\operatorname {sn} (y;k)-\operatorname {cn} (x;k)\operatorname {cn} (y;k)}{1+k^{2}\operatorname {sn} (x;k)\operatorname {sn} (y;k)+\operatorname {dn} (x;k)\operatorname {dn} (y;k)}}

K formulas

Half K formula

\operatorname {sn} \left[{\tfrac {1}{2}}K(k);k\right]={\frac {\sqrt {2}}{{\sqrt {1+k}}+{\sqrt {1-k}}}}

\operatorname {cn} \left[{\tfrac {1}{2}}K(k);k\right]={\frac {{\sqrt {2}}\,{\sqrt[{4}]{1-k^{2}}}}{{\sqrt {1+k}}+{\sqrt {1-k}}}}

\operatorname {dn} \left[{\tfrac {1}{2}}K(k);k\right]={\sqrt[{4}]{1-k^{2}}}

Third K formula

Also this equation^[21] leads to the sn-value of the third of K:

k^{2}s^{4}-2k^{2}s^{3}+2s-1=0

s=\operatorname {sn} {\bigl [}{\tfrac {1}{3}}K(k);k{\bigr ]}

These equations lead to the other values of the Jacobi functions:

\operatorname {cn} {\bigl [}{\tfrac {2}{3}}K(k);k{\bigr ]}=1-\operatorname {sn} {\bigl [}{\tfrac {1}{3}}K(k);k{\bigr ]}

\operatorname {dn} {\bigl [}{\tfrac {2}{3}}K(k);k{\bigr ]}=1/\operatorname {sn} {\bigl [}{\tfrac {1}{3}}K(k);k{\bigr ]}-1

On the basis of that now mentioned quartic equation we can a simplified formula by using the solution algorithm for the General case of the quartic equation. This parametrized formula can be generated in that way:

\operatorname {sn} {\bigl \{}{\tfrac {1}{3}}K{\bigl [}\tan {\bigl (}{\tfrac {1}{2}}\arctan x^{3}{\bigr )}{\bigr ]};\tan {\bigl (}{\tfrac {1}{2}}\arctan x^{3}{\bigr )}{\bigr \}}=\tanh {\Bigl [}{\tfrac {1}{2}}\ln {\Bigl (}{\sqrt {2{\sqrt {x^{4}-x^{2}+1}}-x^{2}+2}}+{\sqrt {x^{2}+1}}{\Bigr )}{\Bigr ]}

The Pythagorean opposite gives that formula successively:

\operatorname {cn} {\bigl \{}{\tfrac {1}{3}}K{\bigl [}\tan {\bigl (}{\tfrac {1}{2}}\arctan x^{3}{\bigr )};\tan {\bigl (}{\tfrac {1}{2}}\arctan x^{3}{\bigr )}{\bigr \}}=\operatorname {sech} {\Bigl [}{\tfrac {1}{2}}\ln {\Bigl (}{\sqrt {2{\sqrt {x^{4}-x^{2}+1}}-x^{2}+2}}+{\sqrt {x^{2}+1}}{\Bigr )}{\Bigr ]}

These two now mentioned formulas are valid for all real values of x, the criterion $x\in \mathbb {R}$ is fulfilled in both equations.

To get x, we take the tangent of twice the arctangent of the modulus and then we take the cube root so that x appears.

And then we insert the generated value x into the right side of the balance of the shown parametrized equations.

In relation to this calculation algorithm, three examples are given below:

First example: ${\tfrac {1}{2}}{\sqrt {2}}=\tan {\bigl [}{\tfrac {1}{2}}\arctan {\bigl (}x^{3}{\bigr )}{\bigr ]}(x={\sqrt {2}}\,)$ If we insert the value $x={\sqrt {2}}\,$ into the fraction showed above, we get this result: $\operatorname {sn} {\bigl [}{\tfrac {1}{3}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}=\tanh {\bigl [}{\tfrac {1}{2}}\ln {\bigl (}{\sqrt[{4}]{12}}+{\sqrt {3}}\,{\bigr )}{\bigr ]}={\tfrac {1}{2}}({\sqrt[{4}]{12}}-{\sqrt {3}}+1)$ $\operatorname {cn} {\bigl [}{\tfrac {1}{3}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}=\operatorname {sech} {\bigl [}{\tfrac {1}{2}}\ln {\bigl (}{\sqrt[{4}]{12}}+{\sqrt {3}}\,{\bigr )}{\bigr ]}={\sqrt[{4}]{2{\sqrt {3}}-3}}$

Second example: ${\tfrac {1}{2}}=\tan {\bigl [}{\tfrac {1}{2}}\arctan {\bigl (}x^{3}{\bigr )}{\bigr ]}(x={\sqrt[{3}]{4/3}}\,)$ If we insert the value $x={\sqrt[{3}]{\tfrac {4}{3}}}\,$ into the fraction showed above, we get this result: $\operatorname {sn} {\bigl [}{\tfrac {1}{3}}K{\bigl (}{\tfrac {1}{2}}{\bigr )};{\tfrac {1}{2}}{\bigr ]}=\tanh {\Bigl [}{\tfrac {1}{2}}\ln {\Bigl (}{\sqrt {2{\sqrt {{\bigl (}{\tfrac {4}{3}}{\bigr )}^{4/3}-{\bigl (}{\tfrac {4}{3}}{\bigr )}^{2/3}+1}}-{\bigl (}{\tfrac {4}{3}}{\bigr )}^{2/3}+2}}+{\sqrt {{\bigl (}{\tfrac {4}{3}}{\bigr )}^{2/3}+1}}\,{\Bigr )}{\Bigr ]}$ $\operatorname {cn} {\bigl [}{\tfrac {1}{3}}K{\bigl (}{\tfrac {1}{2}}{\bigr )};{\tfrac {1}{2}}{\bigr ]}=\operatorname {sech} {\Bigl [}{\tfrac {1}{2}}\ln {\Bigl (}{\sqrt {2{\sqrt {{\bigl (}{\tfrac {4}{3}}{\bigr )}^{4/3}-{\bigl (}{\tfrac {4}{3}}{\bigr )}^{2/3}+1}}-{\bigl (}{\tfrac {4}{3}}{\bigr )}^{2/3}+2}}+{\sqrt {{\bigl (}{\tfrac {4}{3}}{\bigr )}^{2/3}+1}}\,{\Bigr )}{\Bigr ]}$

Third example: ${\tfrac {1}{4}}=\tan {\bigl [}{\tfrac {1}{2}}\arctan {\bigl (}x^{3}{\bigr )}{\bigr ]}(x={\sqrt[{3}]{8/15}}\,)$ If we insert the value $x={\sqrt[{3}]{\tfrac {8}{15}}}\,$ into the fraction showed above, we get this result: $\operatorname {sn} {\bigl [}{\tfrac {1}{3}}K{\bigl (}{\tfrac {1}{4}}{\bigr )};{\tfrac {1}{4}}{\bigr ]}=\tanh {\Bigl [}{\tfrac {1}{2}}\ln {\Bigl (}{\sqrt {2{\sqrt {{\bigl (}{\tfrac {8}{15}}{\bigr )}^{4/3}-{\bigl (}{\tfrac {8}{15}}{\bigr )}^{2/3}+1}}-{\bigl (}{\tfrac {8}{15}}{\bigr )}^{2/3}+2}}+{\sqrt {{\bigl (}{\tfrac {8}{15}}{\bigr )}^{2/3}+1}}\,{\Bigr )}{\Bigr ]}$ $\operatorname {cn} {\bigl [}{\tfrac {1}{3}}K{\bigl (}{\tfrac {1}{4}}{\bigr )};{\tfrac {1}{4}}{\bigr ]}=\operatorname {sech} {\Bigl [}{\tfrac {1}{2}}\ln {\Bigl (}{\sqrt {2{\sqrt {({\tfrac {8}{15}})^{4/3}-({\tfrac {8}{15}})^{2/3}+1}}-({\tfrac {8}{15}})^{2/3}+2}}+{\sqrt {({\tfrac {8}{15}})^{2/3}+1}}\,{\Bigr )}{\Bigr ]}$

Fifth K formula

Following equation has following solution:

4k^{2}t^{6}+8k^{2}t^{5}+2(1-k^{2})^{2}t-(1-k^{2})^{2}=0

t={\tfrac {1}{2}}-{\tfrac {1}{2}}k^{2}\operatorname {sn} {\bigl [}{\tfrac {2}{5}}K(k);k{\bigr ]}^{2}\operatorname {sn} {\bigl [}{\tfrac {4}{5}}K(k);k{\bigr ]}^{2}={\frac {\operatorname {sn} {\bigl [}{\frac {4}{5}}K(k);k{\bigr ]}^{2}-\operatorname {sn} {\bigl [}{\frac {2}{5}}K(k);k{\bigr ]}^{2}}{2\operatorname {sn} {\bigl [}{\frac {2}{5}}K(k);k{\bigr ]}\operatorname {sn} {\bigl [}{\frac {4}{5}}K(k);k{\bigr ]}}}

To get the sn-values, we put the solution x into following expressions:

\operatorname {sn} {\bigl [}{\tfrac {2}{5}}K(k);k{\bigr ]}=(1+k^{2})^{-1/2}{\sqrt {2(1-t-t^{2}){\bigl (}t^{2}+1-t{\sqrt {t^{2}+1}}\,{\bigr )}}}

\operatorname {sn} {\bigl [}{\tfrac {4}{5}}K(k);k{\bigr ]}=(1+k^{2})^{-1/2}{\sqrt {2(1-t-t^{2}){\bigl (}t^{2}+1+t{\sqrt {t^{2}+1}}\,{\bigr )}}}

The t solution between zero and a half is this solution which has to be used for these expressions.

In relation to the now mentioned calculation algorithm, an important example are given below:

This equation of sixth degree is given: $4k^{2}t^{6}+8k^{2}t^{5}+2(1-k^{2})^{2}t-(1-k^{2})^{2}=0$ The value $k={\tfrac {1}{2}}{\sqrt {2}}$ shall be entered in this example. By entering this modulus value and multiplying the whole equation with the factor 4 we get that equation: $8t^{6}+16t^{5}+2t-1=0$ This is the solution of that equation for t that is located between zero and a half: $t={\tfrac {1}{4}}({\sqrt {5}}+1)({\sqrt[{4}]{5}}-1)$ This solution t and the corresponding modulus k will be inserted into the formulas for the amplitude sine values: $\operatorname {sn} {\bigl [}{\tfrac {2}{5}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}=(1+k^{2})^{-1/2}{\sqrt {2(1-t-t^{2})(t^{2}+1-t{\sqrt {t^{2}+1}})}}\,{\bigl [}k={\tfrac {1}{2}}{\sqrt {2}}\,\cap \,t={\tfrac {1}{4}}({\sqrt {5}}+1)({\sqrt[{4}]{5}}-1){\bigr ]}$ $\operatorname {sn} {\bigl [}{\tfrac {4}{5}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}=(1+k^{2})^{-1/2}{\sqrt {2(1-t-t^{2})(t^{2}+1+t{\sqrt {t^{2}+1}})}}\,{\bigl [}k={\tfrac {1}{2}}{\sqrt {2}}\,\cap \,t={\tfrac {1}{4}}({\sqrt {5}}+1)({\sqrt[{4}]{5}}-1){\bigr ]}$ By doing this, following results appear, that are mentioned already in the section of the special values: $\operatorname {sn} {\bigl [}{\tfrac {2}{5}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}{\sqrt[{4}]{2\tan {\tfrac {1}{20}}\pi }}\,{\Bigl (}{\sqrt {\cot {\tfrac {1}{10}}\pi +1}}-{\sqrt {\cot {\tfrac {1}{10}}\pi -3}}{\Bigr )}$ $\operatorname {sn} {\bigl [}{\tfrac {4}{5}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}{\sqrt[{4}]{2\cot {\tfrac {1}{20}}\pi }}\,{\Bigl (}{\sqrt {\cot {\tfrac {1}{10}}\pi +3}}-{\sqrt {\cot {\tfrac {1}{10}}\pi -1}}{\Bigr )}$ By using the hyperbolic functions, these equivalent expressions can be produced: $\operatorname {sn} {\bigl [}{\tfrac {2}{5}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}=\operatorname {sech} {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}\cot {\tfrac {1}{10}}\pi -{\tfrac {1}{2}}{\bigr ]}{\bigr \}}$ $\operatorname {sn} {\bigl [}{\tfrac {4}{5}}K{\bigl (}{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr )};{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}=\operatorname {sech} {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}\cot {\tfrac {1}{10}}\pi +{\tfrac {1}{2}}{\bigr ]}{\bigr \}}$

According to Abel–Ruffini theorem, it is completely impossible to set up elementary expressions for the amplitude sine values of the fifths of the complete first kind elliptic integral for the regular case of the elliptic modulus.

Relations between squares of the functions

Relations between squares of the functions can be derived from two basic relationships (Arguments (u,m) suppressed):

\operatorname {cn} ^{2}+\operatorname {sn} ^{2}=1

\operatorname {cn} ^{2}+m'\operatorname {sn} ^{2}=\operatorname {dn} ^{2}

where m + m' = 1. Multiplying by any function of the form nq yields more general equations:

\operatorname {cq} ^{2}+\operatorname {sq} ^{2}=\operatorname {nq} ^{2}

\operatorname {cq} ^{2}{}+m'\operatorname {sq} ^{2}=\operatorname {dq} ^{2}

With q = d, these correspond trigonometrically to the equations for the unit circle ( $x^{2}+y^{2}=r^{2}$ ) and the unit ellipse ( $x^{2}{}+m'y^{2}=1$ ), with x = cd, y = sd and r = nd. Using the multiplication rule, other relationships may be derived. For example:

-\operatorname {dn} ^{2}{}+m'=-m\operatorname {cn} ^{2}={m\operatorname {sn} ^{2}}{}-m

-m'\operatorname {nd} ^{2}{}+m'=-mm'\operatorname {sd} ^{2}={m\operatorname {cd} ^{2}}-m

m'\operatorname {sc} ^{2}{}+m'=m'\operatorname {nc} ^{2}={\operatorname {dc} ^{2}}-m

\operatorname {cs} ^{2}{}+m'=\operatorname {ds} ^{2}={\operatorname {ns} ^{2}}-m

Representations of the function values via Theta functions

Given are the product definitions of the Jacobi Theta Nullwert Functions as the mathematicians Edmund Taylor Whittaker and George Neville Watson^[22]^[23]^[24] set them up:

\vartheta _{00}(w)=\prod _{n=1}^{\infty }(1-w^{2n})(1+w^{2n-1})^{2}

\vartheta _{01}(w)=\prod _{n=1}^{\infty }(1-w^{2n})(1-w^{2n-1})^{2}

Identities of thirds of the integral $K$ :

With the so-called theta zero-value functions of the elliptic noun of the module, many Jacobian function values can be represented:

\operatorname {sc} [{\tfrac {2}{3}}K(k);k]={\frac {{\sqrt {3}}\,\vartheta _{01}[q(k)^{6}]}{{\sqrt {1-k^{2}}}\,\vartheta _{01}[q(k)^{2}]}}

\operatorname {sn} [{\tfrac {1}{3}}K(k);k]={\frac {2\,\vartheta _{00}[q(k)]^{2}}{3\,\vartheta _{00}[q(k)^{3}]^{2}+\vartheta _{00}[q(k)]^{2}}}={\frac {3\,\vartheta _{01}[q(k)^{3}]^{2}-\vartheta _{01}[q(k)]^{2}}{3\,\vartheta _{01}[q(k)^{3}]^{2}+\vartheta _{01}[q(k)]^{2}}}

\operatorname {cn} [{\tfrac {2}{3}}K(k);k]={\frac {3\,\vartheta _{00}[q(k)^{3}]^{2}-\vartheta _{00}[q(k)]^{2}}{3\,\vartheta _{00}[q(k)^{3}]^{2}+\vartheta _{00}[q(k)]^{2}}}={\frac {2\,\vartheta _{01}[q(k)]^{2}}{3\,\vartheta _{01}[q(k)^{3}]^{2}+\vartheta _{01}[q(k)]^{2}}}

Identities of the fifths of the integral $K$ :

\operatorname {sn} [{\tfrac {1}{5}}K(k);k]={\biggl \{}{\frac {{\sqrt {5}}\,\vartheta _{01}[q(k)^{5}]}{\vartheta _{01}[q(k)]}}-1{\biggr \}}{\biggl \{}{\frac {5\,\vartheta _{01}[q(k)^{10}]^{2}}{\vartheta _{01}[q(k)^{2}]^{2}}}-1{\biggr \}}^{-1}

\operatorname {sn} [{\tfrac {3}{5}}K(k);k]={\biggl \{}{\frac {{\sqrt {5}}\,\vartheta _{01}[q(k)^{5}]}{\vartheta _{01}[q(k)]}}+1{\biggr \}}{\biggl \{}{\frac {5\,\vartheta _{01}[q(k)^{10}]^{2}}{\vartheta _{01}[q(k)^{2}]^{2}}}-1{\biggr \}}^{-1}

\operatorname {cn} [{\tfrac {2}{5}}K(k);k]={\biggl \{}{\frac {{\sqrt {5}}\,\vartheta _{00}[q(k)^{5}]}{\vartheta _{00}[q(k)]}}+1{\biggr \}}{\biggl \{}{\frac {5\,\vartheta _{01}[q(k)^{10}]^{2}}{\vartheta _{01}[q(k)^{2}]^{2}}}-1{\biggr \}}^{-1}

\operatorname {cn} [{\tfrac {4}{5}}K(k);k]={\biggl \{}{\frac {{\sqrt {5}}\,\vartheta _{00}[q(k)^{5}]}{\vartheta _{00}[q(k)]}}-1{\biggr \}}{\biggl \{}{\frac {5\,\vartheta _{01}[q(k)^{10}]^{2}}{\vartheta _{01}[q(k)^{2}]^{2}}}-1{\biggr \}}^{-1}

The elementary combinations of theta zero-value functions and the elliptic nome are not sufficient for the representation of the Jacobian function values of left-hand parenthesis entries beyond rationally broken K-integrals. This requires the theta non-zero functions of the pattern described above.

Jacobi elliptic functions as solutions of nonlinear ordinary differential equations

The derivatives of the three basic Jacobi elliptic functions are:

{\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {sn} (z)=\operatorname {cn} (z)\operatorname {dn} (z),

{\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {cn} (z)=-\operatorname {sn} (z)\operatorname {dn} (z),

{\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {dn} (z)=-m\operatorname {sn} (z)\operatorname {cn} (z).

These can be used to derive the derivatives of all other functions as shown in the table below (arguments (u,m) suppressed):

Derivatives ${\frac {\mathrm {d} }{\mathrm {d} u}}\operatorname {pq} (u,m)$
		q
		c	s	n	d
p
	c	0	−ds ns	−dn sn	−m' nd sd
	s	dc nc	0	cn dn	cd nd
	n	dc sc	−cs ds	0	m cd sd
	d	m' nc sc	−cs ns	−m cn sn	0

With the addition theorems above and for a given m with 0 < m < 1 the major functions are therefore solutions to the following nonlinear ordinary differential equations:

$\operatorname {sn} (x)$ solves the differential equations ${\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}+(1+m)y-2my^{3}=0$ and $\left({\frac {\mathrm {d} y}{\mathrm {d} x}}\right)^{2}=(1-y^{2})(1-my^{2})$
$\operatorname {cn} (x)$ solves the differential equations ${\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}+(1-2m)y+2my^{3}=0$ and $\left({\frac {\mathrm {d} y}{\mathrm {d} x}}\right)^{2}=(1-y^{2})(1-m+my^{2})$
$\operatorname {dn} (x)$ solves the differential equations ${\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}-(2-m)y+2y^{3}=0$ and $\left({\frac {\mathrm {d} y}{\mathrm {d} x}}\right)^{2}=(y^{2}-1)(1-m-y^{2})$

The Jacobi amplitude provides a non-trivial solution of the differential equation describing the exact motion of a simple pendulum. In particular,

\theta =2\operatorname {am} \left({\frac {t{\sqrt {2c}}}{2}},2\right)\rightarrow {\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}+c\sin \theta =0.

A function which solves the above pendulum differential equation with initial angle $\theta _{0}$ is

\theta =2\arcsin(k\operatorname {cd} ({\sqrt {c}}t,k^{2})),\quad k=\sin {\frac {\theta _{0}}{2}}.

Lambert series expansion in terms of the nome

Let the nome be $q=\exp(-\pi K'(m)/K(m))=e^{i\pi \tau }$ , $\operatorname {Im} (\tau )>0$ , $m=k^{2}$ and let $v=\pi u/(2K(m))$ . Then the functions have expansions as Lambert series

\operatorname {sn} (u,m)={\frac {2\pi }{kK(m)}}\sum _{n=0}^{\infty }{\frac {q^{n+1/2}}{1-q^{2n+1}}}\sin((2n+1)v),

\operatorname {cn} (u,m)={\frac {2\pi }{kK(m)}}\sum _{n=0}^{\infty }{\frac {q^{n+1/2}}{1+q^{2n+1}}}\cos((2n+1)v),

\operatorname {dn} (u,m)={\frac {\pi }{2K(m)}}+{\frac {2\pi }{K(m)}}\sum _{n=1}^{\infty }{\frac {q^{n}}{1+q^{2n}}}\cos(2nv)

\operatorname {zn} (u,m)={\frac {2\pi }{K(m)}}\sum _{n=1}^{\infty }{\frac {q^{n}}{1-q^{2n}}}\sin(2nv)

when $q\exp(2\left|\operatorname {Im} (v)\right|)<1$ .

For the Jacobi amplitude,

\operatorname {am} (u,m)={\frac {\pi u}{2K(m)}}+2\sum _{n=1}^{\infty }{\frac {q^{n}}{n(1+q^{2n})}}\sin(2nv)

where $0<m<1$ and $u\in \mathbb {R}$ .

Bivariate power series expansions have been published by Schett.^[25]

Fast computation

The theta function ratios provide an efficient way of computing the Jacobi elliptic functions. There is an alternative method, based on the arithmetic-geometric mean and Landen's transformations:^[6]

Initialize

a_{0}=1,\,b_{0}={\sqrt {1-m}},c_{0}={\sqrt {1-b_{0}^{2}}}

where $0<m<1$ . Define

a_{n}={\frac {a_{n-1}+b_{n-1}}{2}},\,b_{n}={\sqrt {a_{n-1}b_{n-1}}},\,c_{n}={\frac {a_{n-1}-b_{n-1}}{2}}

where $n\geq 1$ . Then define

\varphi _{N}=2^{N}a_{N}u

for $u\in \mathbb {R}$ and a fixed $N\in \mathbb {N}$ . If

\varphi _{n-1}={\frac {1}{2}}\left(\varphi _{n}+\arcsin \left({\frac {c_{n}}{a_{n}}}\sin \varphi _{n}\right)\right)

for $n\geq 1$ , then

\operatorname {am} (u,m)=\varphi _{0}

as $N\to \infty$ . This is notable for its rapid convergence. It is then trivial to compute all Jacobi elliptic functions from the Jacobi amplitude $\operatorname {am}$ on the real line.

In conjunction with the addition theorems for elliptic functions (which hold for complex numbers in general) and the Jacobi transformations, the method of computation described above can be used to compute all Jacobi elliptic functions in the whole complex plane.

Another method of fast computation of the Jacobi elliptic functions via the arithmetic–geometric mean, avoiding the computation of the Jacobi amplitude, is due to Herbert E. Salzer:^[26]

Let

0\leq m\leq 1,\,0\leq u\leq K(m),\,a_{0}=1,\,b_{0}={\sqrt {1-m}},

a_{n+1}={\frac {a_{n}+b_{n}}{2}},\,b_{n+1}={\sqrt {a_{n}b_{n}}},\,c_{n+1}={\frac {a_{n}-b_{n}}{2}}.

Set

{\begin{aligned}y_{N}&={\frac {a_{N}}{\sin(a_{N}u)}}\\y_{N-1}&=y_{N}+{\frac {a_{N}c_{N}}{y_{N}}}\\y_{N-2}&=y_{N-1}+{\frac {a_{N-1}c_{N-1}}{y_{N-1}}}\\&\,\,\,\vdots \\y_{0}&=y_{1}+{\frac {m}{4y_{1}}}.\end{aligned}}

Then

{\begin{aligned}\operatorname {sn} (u,m)&={\frac {1}{y_{0}}}\\\operatorname {cn} (u,m)&={\sqrt {1-{\frac {1}{y_{0}^{2}}}}}\\\operatorname {dn} (u,m)&={\sqrt {1-{\frac {m}{y_{0}^{2}}}}}\end{aligned}}

as $N\to \infty$ .

Approximation in terms of hyperbolic functions

The Jacobi elliptic functions can be expanded in terms of the hyperbolic functions. When $m$ is close to unity, such that $m'^{2}$ and higher powers of $m'$ can be neglected, we have:^[27]^[28]

sn(u): $\operatorname {sn} (u,m)\approx \tanh(u)+{\frac {1}{4}}m'(\sinh(u)\cosh(u)-u)\operatorname {sech} ^{2}(u).$
cn(u): $\operatorname {cn} (u,m)\approx \operatorname {sech} (u)-{\frac {1}{4}}m'(\sinh(u)\cosh(u)-u)\tanh(u)\operatorname {sech} (u).$
dn(u): $\operatorname {dn} (u,m)\approx \operatorname {sech} (u)+{\frac {1}{4}}m'(\sinh(u)\cosh(u)+u)\tanh(u)\operatorname {sech} (u).$

For the Jacobi amplitude,

\operatorname {am} (u,m)\approx \operatorname {gd} (u)+{\frac {1}{4}}m'(\sinh(u)\cosh(u)-u)\operatorname {sech} (u).

Continued fractions

Assuming real numbers $a,p$ with $0<a<p$ and the nome $q=e^{\pi i\tau }$ , $\operatorname {Im} (\tau )>0$ with elliptic modulus ${\textstyle k(\tau )={\sqrt {1-k'(\tau )^{2}}}=(\vartheta _{10}(0;\tau )/\vartheta _{00}(0;\tau ))^{2}}$ . If $K[\tau ]=K(k(\tau ))$ , where $K(x)=\pi /2\cdot {}_{2}F_{1}(1/2,1/2;1;x^{2})$ is the complete elliptic integral of the first kind, then holds the following continued fraction expansion^[29]

{\begin{aligned}&{\frac {{\textrm {dn}}\left((p/2-a)\tau K\left[{\frac {p\tau }{2}}\right];k\left({\frac {p\tau }{2}}\right)\right)}{\sqrt {k'\left({\frac {p\tau }{2}}\right)}}}={\frac {\sum _{n=-\infty }^{\infty }q^{p/2n^{2}+(p/2-a)n}}{\sum _{n=-\infty }^{\infty }(-1)^{n}q^{p/2n^{2}+(p/2-a)n}}}\\[4pt]={}&-1+{\frac {2}{1-{}}}\,{\frac {q^{a}+q^{p-a}}{1-q^{p}+{}}}\,{\frac {(q^{a}+q^{2p-a})(q^{a+p}+q^{p-a})}{1-q^{3p}+{}}}\,{\frac {q^{p}(q^{a}+q^{3p-a})(q^{a+2p}+q^{p-a})}{1-q^{5p}+{}}}\,{\frac {q^{2p}(q^{a}+q^{4p-a})(q^{a+3p}+q^{p-a})}{1-q^{7p}+{}}}\cdots \end{aligned}}

Known continued fractions involving ${\textrm {sn}}(t),{\textrm {cn}}(t)$ and ${\textrm {dn}}(t)$ with elliptic modulus $k$ are

For $z\in \mathbb {C}$ , $|k|<1$ :^[30] pg. 374

\int _{0}^{\infty }{\textrm {sn}}(t)e^{-tz}\,\mathrm {d} t={\frac {1}{1^{2}(1+k^{2})+z^{2}-{}}}\,{\frac {1\cdot 2^{2}\cdot 3k^{2}}{3^{2}(1+k^{2})+z^{2}-{}}}\,{\frac {3\cdot 4^{2}\cdot 5k^{2}}{5^{2}(1+k^{2})+z^{2}-{}}}\cdots

For $z\in \mathbb {C} \setminus \{0\}$ , $|k|<1$ :^[30] pg. 375

\int _{0}^{\infty }{\textrm {sn}}^{2}(t)e^{-tz}\,\mathrm {d} t={\frac {2z^{-1}}{2^{2}(1+k^{2})+z^{2}-{}}}\,{\frac {2\cdot 3^{2}\cdot 4k^{2}}{4^{2}(1+k^{2})+z^{2}-{}}}\,{\frac {4\cdot 5^{2}\cdot 6k^{2}}{6^{2}(1+k^{2})+z^{2}-{}}}\cdots

For $z\in \mathbb {C} \setminus \{0\}$ , $|k|<1$ :^[31] pg. 220

\int _{0}^{\infty }{\textrm {cn}}(t)e^{-tz}\,\mathrm {d} t={\frac {1}{z+{}}}\,{\frac {1^{2}}{z+{}}}\,{\frac {2^{2}k^{2}}{z+{}}}\,{\frac {3^{2}}{z+{}}}\,{\frac {4^{2}k^{2}}{z+{}}}\,{\frac {5^{2}}{z+{}}}\cdots

For $z\in \mathbb {C} \setminus \{0\}$ , $|k|<1$ :^[30] pg. 374

\int _{0}^{\infty }{\textrm {dn}}(t)e^{-tz}\,\mathrm {d} t={\frac {1}{z+{}}}\,{\frac {1^{2}k^{2}}{z+{}}}\,{\frac {2^{2}}{z+{}}}\,{\frac {3^{2}k^{2}}{z+{}}}\,{\frac {4^{2}}{z+{}}}\,{\frac {5^{2}k^{2}}{z+{}}}\cdots

For $z\in \mathbb {C}$ , $|k|<1$ :^[30] pg. 375

\int _{0}^{\infty }{\frac {{\textrm {sn}}(t){\textrm {cn}}(t)}{{\textrm {dn}}(t)}}e^{-tz}\,\mathrm {d} t={\frac {1}{2\cdot 1^{2}(2-k^{2})+z^{2}-{}}}\,{\frac {1\cdot 2^{2}\cdot 3k^{4}}{2\cdot 3^{2}(2-k^{2})+z^{2}-{}}}\,{\frac {3\cdot 4^{2}\cdot 5k^{4}}{2\cdot 5^{2}(2-k^{2})+z^{2}-{}}}\cdots

Inverse functions

The inverses of the Jacobi elliptic functions can be defined similarly to the inverse trigonometric functions; if $x=\operatorname {sn} (\xi ,m)$ , $\xi =\operatorname {arcsn} (x,m)$ . They can be represented as elliptic integrals,^[32]^[33]^[34] and power series representations have been found.^[35]^[3]

$\operatorname {arcsn} (x,m)=\int _{0}^{x}{\frac {\mathrm {d} t}{\sqrt {(1-t^{2})(1-mt^{2})}}}$
$\operatorname {arccn} (x,m)=\int _{x}^{1}{\frac {\mathrm {d} t}{\sqrt {(1-t^{2})(1-m+mt^{2})}}}$
$\operatorname {arcdn} (x,m)=\int _{x}^{1}{\frac {\mathrm {d} t}{\sqrt {(1-t^{2})(t^{2}+m-1)}}}$

Map projection

The Peirce quincuncial projection is a map projection based on Jacobian elliptic functions.

Notes

↑ If $u\in \mathbb {R}$ and $m$ is restricted to $[0,1]$ , then $\operatorname {dn} (u,m)$ can be also written as ${\sqrt {1-m\sin ^{2}\operatorname {am} (u,m)}}.$

References

Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. "Chapter 16". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 569. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
Jonathan M. Borwein, Peter B. Borwein: Pi and the AGM. A study in analytical Number Theory and Computational Complexity. John Wiley & Sons, 1987.
N. I. Akhiezer, Elements of the Theory of Elliptic Functions (1970) Moscow, translated into English as AMS Translations of Mathematical Monographs Volume 79 (1990) AMS, Rhode Island ISBN 0-8218-4532-2
A. C. Dixon The elementary properties of the elliptic functions, with examples (Macmillan, 1894)
Alfred George Greenhill The applications of elliptic functions (London, New York, Macmillan, 1892)
Edmund T. Whittaker, George Neville Watson: A Course in Modern Analysis. 4th ed. Cambridge, England: Cambridge University Press, 1990. pp. 469–470.
H. Hancock Lectures on the theory of elliptic functions (New York, J. Wiley & sons, 1910)
Jacobi, C. G. J. (1829), Fundamenta nova theoriae functionum ellipticarum (in Latin), Königsberg, ISBN 978-1-108-05200-9, Reprinted by Cambridge University Press 2012
Reinhardt, William P.; Walker, Peter L. (2010), "Jacobian Elliptic Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
(in French) P. Appell and E. Lacour Principes de la théorie des fonctions elliptiques et applications (Paris, Gauthier Villars, 1897)
(in French) G. H. Halphen Traité des fonctions elliptiques et de leurs applications (vol. 1) (Paris, Gauthier-Villars, 1886–1891)
(in French) G. H. Halphen Traité des fonctions elliptiques et de leurs applications (vol. 2) (Paris, Gauthier-Villars, 1886–1891)
(in French) G. H. Halphen Traité des fonctions elliptiques et de leurs applications (vol. 3) (Paris, Gauthier-Villars, 1886–1891)
(in French) J. Tannery and J. Molk Eléments de la théorie des fonctions elliptiques. Tome I, Introduction. Calcul différentiel. Ire partie (Paris : Gauthier-Villars et fils, 1893)
(in French) J. Tannery and J. Molk Eléments de la théorie des fonctions elliptiques. Tome II, Calcul différentiel. IIe partie (Paris : Gauthier-Villars et fils, 1893)
(in French) J. Tannery and J. Molk Eléments de la théorie des fonctions elliptiques. Tome III, Calcul intégral. Ire partie, Théorèmes généraux. Inversion (Paris : Gauthier-Villars et fils, 1893)
(in French) J. Tannery and J. Molk Eléments de la théorie des fonctions elliptiques. Tome IV, Calcul intégral. IIe partie, Applications (Paris : Gauthier-Villars et fils, 1893)
(in French) C. Briot and J. C. Bouquet Théorie des fonctions elliptiques (Paris : Gauthier-Villars, 1875)
Toshio Fukushima: Fast Computation of Complete Elliptic Integrals and Jacobian Elliptic Functions. 2012, National Astronomical Observatory of Japan (国立天文台)
Lowan, Blanch und Horenstein: On the Inversion of the q-Series Associated with Jacobian Elliptic Functions. Bull. Amer. Math. Soc. 48, 1942
H. Ferguson, D. E. Nielsen, G. Cook: A partition formula for the integer coefficients of the theta function nome. Mathematics of computation, Volume 29, Nummer 131, July 1975
J. D. Fenton and R. S. Gardiner-Garden: Rapidly-convergent methods for evaluating elliptic integrals and theta and elliptic functions. J. Austral. Math. Soc. (Series B) 24, 1982, p. 57
Adolf Kneser: Neue Untersuchung einer Reihe aus der Theorie der elliptischen Funktionen. J. reine u. angew. Math. 157, 1927. pages 209 – 218

External links

"Jacobi elliptic functions", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Weisstein, Eric W. "Jacobi Elliptic Functions". MathWorld.

↑ Armitage, J. V.; Eberlein, W. F. (2006). Elliptic Functions (First ed.). Cambridge University Press. ISBN 978-0-521-78078-0. p. 48
1 2 Walker, Peter (2003). "The Analyticity of Jacobian Functions with Respect to the Parameter k". Proceedings of the Royal Society. 459 (2038): 2569–2574. Bibcode:2003RSPSA.459.2569W. doi:10.1098/rspa.2003.1157. JSTOR 3560143. S2CID 121368966.
1 2 3 4 5 Olver, F. W. J.; et al., eds. (2017-12-22). "NIST Digital Library of Mathematical Functions (Release 1.0.17)". National Institute of Standards and Technology. Retrieved 2018-02-26.
↑ "cplot, Python package for plotting complex-valued functions". GitHub.
1 2 3 4 5 6 Neville, Eric Harold (1944). Jacobian Elliptic Functions. Oxford: Oxford University Press.
1 2 Sala, Kenneth L. (November 1989). "Transformations of the Jacobian Amplitude Function and Its Calculation via the Arithmetic-Geometric Mean". SIAM Journal on Mathematical Analysis. 20 (6): 1514–1528. doi:10.1137/0520100.
↑ Reinhardt, W. P.; Walker, P. L. (2010), "Jacobian Elliptic Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
↑ Carlson, B. C. (2010), "Elliptic Integrals", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
↑ Whittaker and Watson (1990) pp. 469–470
↑ Alvaro H. Salas, Lorenzo J. H. Martinez, David L. R. Ocampo R. (2021-10-11), "Approximation of Elliptic Functions by Means of Trigonometric Functions with Applications", Mathematical Problems in Engineering, vol. 2021, pp. e5546666, doi:10.1155/2021/5546666, ISSN 1024-123X{{citation}}: CS1 maint: multiple names: authors list (link)
↑ "Table of Infinite Products Infinite Sums Infinite Series Elliptic Theta". Retrieved 2021-08-31.
↑ "A002103 - OEIS". Retrieved 2023-05-28.
↑ "Series Expansion of EllipticNomeQ differs from older Mathematica Version". Retrieved 2023-05-28.
↑ R. B. King, E. R. Canfield (1992-08-01), "Icosahedral symmetry and the quintic equation", Computers & Mathematics with Applications, vol. 24, no. 3, pp. 13–28, doi:10.1016/0898-1221(92)90210-9, ISSN 0898-1221
↑ Karl Heinrich Schellbach (1864), Die Lehre von den Elliptischen Integralen und den ThetaFunctionen, G. Reimer, retrieved 2023-06-11
↑ Adolf Kneser (1927), "Neue Untersuchung einer Reihe aus der Theorie der elliptischen Funktionen.", Journal für die reine und angewandte Mathematik, vol. 158, pp. 209–218, ISSN 0075-4102, retrieved 2023-06-11
↑ D. K. Lee (1989-03-01), Application of theta functions for numerical evaluation of complete elliptic integrals of the first and second kinds, Oak Ridge National Lab. (ORNL), Oak Ridge, TN (United States), doi:10.2172/6137964, OSTI 6137964, retrieved 2023-06-11
1 2 3 4 5 6 "Introduction to the Jacobi elliptic functions". The Wolfram Functions Site. Wolfram Research, Inc. 2018. Retrieved January 7, 2018.
↑ Whittaker, E.T.; Watson, G.N. (1940). A Course in Modern Analysis. New York, USA: The MacMillan Co. ISBN 978-0-521-58807-2.
↑ "Elliptic Functions: Complex Variables".
1 2 Viktor Prasolov and Yuri Soloviev (1997), "Elliptic Functions and Elliptic Integrals" (PDF), arXiv: General Mathematics, retrieved 2023-06-24
↑ Weisstein, Eric W. "Jacobi Theta Functions". MathWorld.
↑ Borwein, Jonathan M.; Borwein, Peter B. (1998). Pi and the AGM: a study in analytic number theory and computational complexity (PDF). New York: Wiley. ISBN 978-0471315155.
↑ "DLMF: 20.5 Infinite Products and Related Results". Retrieved 2022-08-13.
↑ Schett, Alois (1976). "Properties of the Taylor series expansion coefficients of the Jacobian Elliptic Functions". Math. Comp. 30 (133): 143–147. doi:10.1090/S0025-5718-1976-0391477-3. MR 0391477. S2CID 120666361.
↑ Salzer, Herbert E. (July 1962). "Quick calculation of Jacobian elliptic functions". Communications of the ACM. 5 (7): 399. doi:10.1145/368273.368573. S2CID 44953400.
↑ Reinhardt, W. P.; Walker, P. L. (2010), "Jacobian Elliptic Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
↑ Reinhardt, W. P.; Walker, P. L. (2010), "Jacobian Elliptic Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
↑ N.Bagis.(2020)."Evaluations of series related to Jacobi elliptic functions". preprint https://www.researchgate.net/publication/331370071_Evaluations_of_Series_Related_to_Jacobi_Elliptic_Functions
1 2 3 4 H.S. Wall. (1948). "Analytic Theory of Continued Fractions", Van Nostrand, New York.
↑ Perron, O. (1957). "Die Lehre von den Kettenbruchen", Band II, B.G. Teubner, Stuttgart.
↑ Reinhardt, W. P.; Walker, P. L. (2010), "§22.15 Inverse Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
↑ Ehrhardt, Wolfgang. "The AMath and DAMath Special Functions: Reference Manual and Implementation Notes" (PDF). p. 42. Archived from the original (PDF) on 31 July 2016. Retrieved 17 July 2013.
↑ Byrd, P.F.; Friedman, M.D. (1971). Handbook of Elliptic Integrals for Engineers and Scientists (2nd ed.). Berlin: Springer-Verlag.
↑ Carlson, B. C. (2008). "Power series for inverse Jacobian elliptic functions" (PDF). Mathematics of Computation. 77 (263): 1615–1621. Bibcode:2008MaCom..77.1615C. doi:10.1090/s0025-5718-07-02049-2. Retrieved 17 July 2013.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[6] If $u\in \mathbb {R}$ and $m$ is restricted to $[0,1]$ , then $\operatorname {dn} (u,m)$ can be also written as ${\sqrt {1-m\sin ^{2}\operatorname {am} (u,m)}}.$

[1] Armitage, J. V.; Eberlein, W. F. (2006). Elliptic Functions (First ed.). Cambridge University Press. ISBN 978-0-521-78078-0. p. 48

[Walker-2] 1 2 Walker, Peter (2003). "The Analyticity of Jacobian Functions with Respect to the Parameter k". Proceedings of the Royal Society. 459 (2038): 2569–2574. Bibcode:2003RSPSA.459.2569W. doi:10.1098/rspa.2003.1157. JSTOR 3560143. S2CID 121368966.

[DLMF22-3] 1 2 3 4 5 Olver, F. W. J.; et al., eds. (2017-12-22). "NIST Digital Library of Mathematical Functions (Release 1.0.17)". National Institute of Standards and Technology. Retrieved 2018-02-26.

[4] "cplot, Python package for plotting complex-valued functions". GitHub.

[Neville1944-5] 1 2 3 4 5 6 Neville, Eric Harold (1944). Jacobian Elliptic Functions. Oxford: Oxford University Press.

[sala-7] 1 2 Sala, Kenneth L. (November 1989). "Transformations of the Jacobian Amplitude Function and Its Calculation via the Arithmetic-Geometric Mean". SIAM Journal on Mathematical Analysis. 20 (6): 1514–1528. doi:10.1137/0520100.

[8] Reinhardt, W. P.; Walker, P. L. (2010), "Jacobian Elliptic Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.

[9] Carlson, B. C. (2010), "Elliptic Integrals", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.

[10] Whittaker and Watson (1990) pp. 469–470

[11] Alvaro H. Salas, Lorenzo J. H. Martinez, David L. R. Ocampo R. (2021-10-11), "Approximation of Elliptic Functions by Means of Trigonometric Functions with Applications", Mathematical Problems in Engineering, vol. 2021, pp. e5546666, doi:10.1155/2021/5546666, ISSN 1024-123X{{citation}}: CS1 maint: multiple names: authors list (link)

[12] "Table of Infinite Products Infinite Sums Infinite Series Elliptic Theta". Retrieved 2021-08-31.

[13] "A002103 - OEIS". Retrieved 2023-05-28.

[14] "Series Expansion of EllipticNomeQ differs from older Mathematica Version". Retrieved 2023-05-28.

[15] R. B. King, E. R. Canfield (1992-08-01), "Icosahedral symmetry and the quintic equation", Computers & Mathematics with Applications, vol. 24, no. 3, pp. 13–28, doi:10.1016/0898-1221(92)90210-9, ISSN 0898-1221

[16] Karl Heinrich Schellbach (1864), Die Lehre von den Elliptischen Integralen und den ThetaFunctionen, G. Reimer, retrieved 2023-06-11

[17] Adolf Kneser (1927), "Neue Untersuchung einer Reihe aus der Theorie der elliptischen Funktionen.", Journal für die reine und angewandte Mathematik, vol. 158, pp. 209–218, ISSN 0075-4102, retrieved 2023-06-11

[18] D. K. Lee (1989-03-01), Application of theta functions for numerical evaluation of complete elliptic integrals of the first and second kinds, Oak Ridge National Lab. (ORNL), Oak Ridge, TN (United States), doi:10.2172/6137964, OSTI 6137964, retrieved 2023-06-11

[WolframJE-19] 1 2 3 4 5 6 "Introduction to the Jacobi elliptic functions". The Wolfram Functions Site. Wolfram Research, Inc. 2018. Retrieved January 7, 2018.

[W&W-20] Whittaker, E.T.; Watson, G.N. (1940). A Course in Modern Analysis. New York, USA: The MacMillan Co. ISBN 978-0-521-58807-2.

[21] "Elliptic Functions: Complex Variables".

[auto-22] 1 2 Viktor Prasolov and Yuri Soloviev (1997), "Elliptic Functions and Elliptic Integrals" (PDF), arXiv: General Mathematics, retrieved 2023-06-24

[23] Weisstein, Eric W. "Jacobi Theta Functions". MathWorld.

[24] Borwein, Jonathan M.; Borwein, Peter B. (1998). Pi and the AGM: a study in analytic number theory and computational complexity (PDF). New York: Wiley. ISBN 978-0471315155.

[25] "DLMF: 20.5 Infinite Products and Related Results". Retrieved 2022-08-13.

[26] Schett, Alois (1976). "Properties of the Taylor series expansion coefficients of the Jacobian Elliptic Functions". Math. Comp. 30 (133): 143–147. doi:10.1090/S0025-5718-1976-0391477-3. MR 0391477. S2CID 120666361.

[27] Salzer, Herbert E. (July 1962). "Quick calculation of Jacobian elliptic functions". Communications of the ACM. 5 (7): 399. doi:10.1145/368273.368573. S2CID 44953400.

[28] Reinhardt, W. P.; Walker, P. L. (2010), "Jacobian Elliptic Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.

[29] Reinhardt, W. P.; Walker, P. L. (2010), "Jacobian Elliptic Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.

[bagis-evaluations-30] N.Bagis.(2020)."Evaluations of series related to Jacobi elliptic functions". preprint https://www.researchgate.net/publication/331370071_Evaluations_of_Series_Related_to_Jacobi_Elliptic_Functions

[wall-analytic-theory-31] 1 2 3 4 H.S. Wall. (1948). "Analytic Theory of Continued Fractions", Van Nostrand, New York.

[perron-32] Perron, O. (1957). "Die Lehre von den Kettenbruchen", Band II, B.G. Teubner, Stuttgart.

[33] Reinhardt, W. P.; Walker, P. L. (2010), "§22.15 Inverse Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.

[34] Ehrhardt, Wolfgang. "The AMath and DAMath Special Functions: Reference Manual and Implementation Notes" (PDF). p. 42. Archived from the original (PDF) on 31 July 2016. Retrieved 17 July 2013.

[35] Byrd, P.F.; Friedman, M.D. (1971). Handbook of Elliptic Integrals for Engineers and Scientists (2nd ed.). Berlin: Springer-Verlag.

[36] Carlson, B. C. (2008). "Power series for inverse Jacobian elliptic functions" (PDF). Mathematics of Computation. 77 (263): 1615–1621. Bibcode:2008MaCom..77.1615C. doi:10.1090/s0025-5718-07-02049-2. Retrieved 17 July 2013.

[1]

[2]

[3]

[4]

[5]

[note 1]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

Overview

Notation

Definition in terms of inverses of elliptic integrals

Definition as trigonometry: the Jacobi ellipse

Definition in terms of Jacobi theta functions

Jacobi theta function description

Jacobi zn function

Comparison between sums and products

The elliptic nome and its series

Elliptic integral and elliptic nome

Kneser integer sequence

Schellbach Schwarz integer sequence

Definition in terms of Neville theta functions

Jacobi transformations

The Jacobi imaginary transformations

The Jacobi real transformations

Other Jacobi transformations

The Jacobi hyperbola

Minor functions

Periodicity, poles, and residues

Special values

Lemniscatic values

Equianharmonic values

Elementary functions

Identities

Addition theorems

Half Angle formula

K formulas

Relations between squares of the functions

Representations of the function values via Theta functions

Jacobi elliptic functions as solutions of nonlinear ordinary differential equations

Lambert series expansion in terms of the nome

Fast computation

Approximation in terms of hyperbolic functions

Continued fractions

Inverse functions

Map projection

See also

Notes

References

External links