Tetrahedron with a right-angle corner in O

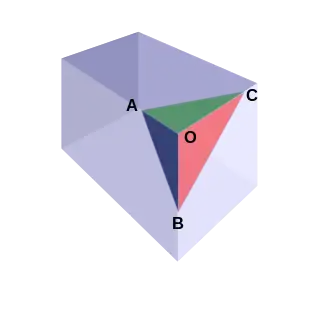
In mathematics, De Gua's theorem is a three-dimensional analog of the Pythagorean theorem named after Jean Paul de Gua de Malves. It states that if a tetrahedron has a right-angle corner (like the corner of a cube), then the square of the area of the face opposite the right-angle corner is the sum of the squares of the areas of the other three faces:

$${\displaystyle A_{ABC}^{2}=A_{\color {blue}ABO}^{2}+A_{\color {green}ACO}^{2}+A_{\color {red}BCO}^{2}}$$

De Gua's theorem can be applied for proving a special case of Heron's formula.^[1]

Generalizations

The Pythagorean theorem and de Gua's theorem are special cases (n = 2, 3) of a general theorem about n-simplices with a right-angle corner, proved by P. S. Donchian and H. S. M. Coxeter in 1935.^[2] This, in turn, is a special case of a yet more general theorem by Donald R. Conant and William A. Beyer (1974),^[3] which can be stated as follows.

Let U be a measurable subset of a k-dimensional affine subspace of ${\displaystyle \mathbb {R} ^{n}}$ (so ${\displaystyle k\leq n}$). For any subset ${\displaystyle I\subseteq \{1,\ldots ,n\}}$ with exactly k elements, let ${\displaystyle U_{I}}$ be the orthogonal projection of U onto the linear span of ${\displaystyle e_{i_{1}},\ldots ,e_{i_{k}}}$, where ${\displaystyle I=\{i_{1},\ldots ,i_{k}\}}$ and ${\displaystyle e_{1},\ldots ,e_{n}}$ is the standard basis for ${\displaystyle \mathbb {R} ^{n}}$. Then

$${\displaystyle \operatorname {vol} _{k}^{2}(U)=\sum _{I}\operatorname {vol} _{k}^{2}(U_{I}),}$$

where ${\displaystyle \operatorname {vol} _{k}(U)}$ is the k-dimensional volume of U and the sum is over all subsets ${\displaystyle I\subseteq \{1,\ldots ,n\}}$ with exactly k elements.

De Gua's theorem and its generalisation (above) to n-simplices with right-angle corners correspond to the special case where k = n−1 and U is an (n−1)-simplex in ${\displaystyle \mathbb {R} ^{n}}$ with vertices on the co-ordinate axes. For example, suppose n = 3, k = 2 and U is the triangle ${\displaystyle \triangle ABC}$ in ${\displaystyle \mathbb {R} ^{3}}$ with vertices A, B and C lying on the ${\displaystyle x_{1}}$-, ${\displaystyle x_{2}}$- and ${\displaystyle x_{3}}$-axes, respectively. The subsets ${\displaystyle I}$ of ${\displaystyle \{1,2,3\}}$ with exactly 2 elements are ${\displaystyle \{2,3\}}$, ${\displaystyle \{1,3\}}$ and ${\displaystyle \{1,2\}}$. By definition, ${\displaystyle U_{\{2,3\}}}$ is the orthogonal projection of ${\displaystyle U=\triangle ABC}$ onto the ${\displaystyle x_{2}x_{3}}$-plane, so ${\displaystyle U_{\{2,3\}}}$ is the triangle ${\displaystyle \triangle OBC}$ with vertices O, B and C, where O is the origin of ${\displaystyle \mathbb {R} ^{3}}$. Similarly, ${\displaystyle U_{\{1,3\}}=\triangle AOC}$ and ${\displaystyle U_{\{1,2\}}=\triangle ABO}$, so the Conant–Beyer theorem says

$${\displaystyle \operatorname {vol} _{2}^{2}(\triangle ABC)=\operatorname {vol} _{2}^{2}(\triangle OBC)+\operatorname {vol} _{2}^{2}(\triangle AOC)+\operatorname {vol} _{2}^{2}(\triangle ABO),}$$

which is de Gua's theorem.

The generalisation of de Gua's theorem to n-simplices with right-angle corners can also be obtained as a special case from the Cayley–Menger determinant formula.

De Gua's theorem can also be generalized to arbitrary tetrahedra and to pyramids.^[4][5]

History

Jean Paul de Gua de Malves (1713–1785) published the theorem in 1783, but around the same time a slightly more general version was published by another French mathematician, Charles de Tinseau d'Amondans (1746–1818), as well. However the theorem had also been known much earlier to Johann Faulhaber (1580–1635) and René Descartes (1596–1650).^[6][7]

See also

• Vector area and projected area
• Bivector

Notes

References

• Sergio A. Alvarez: Note on an n-dimensional Pythagorean theorem, Carnegie Mellon University.
• Hull, Lewis; Perfect, Hazel; Heading, J. (1978). "62.23 Pythagoras in Higher Dimensions: Three Approaches". Mathematical Gazette. 62 (421): 206–211. doi:10.2307/3616695. JSTOR 3616695. S2CID 187356402.
• Weisstein, Eric W. "de Gua's theorem". MathWorld.