
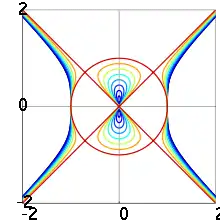
In geometry, a Devil's curve, also known as the Devil on Two Sticks, is a curve defined in the Cartesian plane by an equation of the form
The polar equation of this curve is of the form
- .
Devil's curves were discovered in 1750 by Gabriel Cramer, who studied them extensively.[2]
The name comes from the shape its central lemniscate takes when graphed. The shape is named after the juggling game diabolo, which was named after the Devil[3] and which involves two sticks, a string, and a spinning prop in the likeness of the lemniscate.[4]
For , the central lemniscate, often called hourglass, is horizontal. For it is vertical. If , the shape becomes a circle. The vertical hourglass intersects the y-axis at . The horizontal hourglass intersects the x-axis at .
Electric Motor Curve
A special case of the Devil's curve occurs at , where the curve is called the electric motor curve.[5] It is defined by an equation of the form
.
The name of the special case comes from the middle shape's resemblance to the coils of wire, which rotate from forces exerted by magnets surrounding it.
References
- ↑ "Devil's Curve". Wolfram MathWorld.
- ↑ Introduction a l'analyse des lignes courbes algébriques, p. 19 (Genova, 1750).
- ↑ "Diabolo Patent". Retrieved 16 July 2013.
- ↑ Wassenaar, Jan. "devil's curve". www.2dcurves.com. Retrieved 2018-02-26.
- ↑ Mathematical Models, p. 71 (Cundy and Rollet. 1961)