Extract from Diego Ortiz's El Primo Libro ... Nel qual si tratta delle Glose depicting rhythm and generic intervals. Observe the diminution (i.e. division) process suggested by the composer, in reference to the rhythmic figures in the upper and lower musical parts.
A realization of the bottom line of the above Diego Ortiz extract in modern notation, completed with an arbitrarily chosen clef and a time signature. Playⓘ

In Western music and music theory, diminution (from Medieval Latin diminutio, alteration of Latin deminutio, decrease) has four distinct meanings. Diminution may be a form of embellishment in which a long note is divided into a series of shorter, usually melodic, values (also called "coloration"; Ger. Kolorieren). Diminution may also be the compositional device where a melody, theme or motif is presented in shorter note-values than were previously used. Diminution is also the term for the proportional shortening of the value of individual note-shapes in mensural notation, either by coloration or by a sign of proportion. A minor or perfect interval that is narrowed by a chromatic semitone is a diminished interval, and the process may be referred to as diminution (this, too, was sometimes referred to as "coloration").

Diminution as embellishment

Diminution is a form of embellishment or melodic variation in which a long note or a series of long notes is divided into shorter, usually melodic, values, as in the similar practices of breaking or division in England, passaggio in Italy, double in France and glosas or diferencias in Spain.[1] It is thoroughly documented in written sources of the sixteenth, seventeenth and early eighteenth centuries, and enjoyed a remarkable flowering in Venice from about 1580–1620. It is an integral aspect of modern performance practice; Donington describes the consequences of failing to add "necessary figuration" as "disastrous".[2]: 152 

Italian literature of the sixteenth and early seventeenth century

Spanish literature

English literature

German literature

Dutch literature

For Heinrich Schenker, "all foreground is diminution".[4] "All diminution must be secured firmly to the total work by means which are precisely demonstrable and organically verified by the inner necessities of the voice-leading".[5] This conception has been essential to Schenker's theory from some of his earliest writings.[6] In Schenkerian analysis a diminution is an elaboration by which an event formed of notes of longer value is expressed in notes of smaller value. See nonchord tone.

Diminution in composition

A melody or series of notes is diminished if the lengths of the notes are shortened; diminution is thus the opposite of augmentation, where the notes are lengthened. A melody originally consisting of four crotchets (quarter-notes) for example, is diminished if it later appears with four quavers (eighth-notes) instead. In the following theme from Beethoven's Leonora no. 3 Overture, the melodic ideas in bars 3 and 5 recur at twice the speed in bars 7-8:

Leonora no 3

This technique is often used in contrapuntal music, as in the "canon by diminution" ("per diminutionem"), in which the notes in the following voice or voices are shorter than those in the leading voice, usually half the length.[7]

Contrapuntus VII from Bach's Art of Fugue. Observe the lower voice of the canon in halved (i.e. diminished) note values.

In jazz, Thelonious Monk's composition "Brilliant Corners" consists of a theme that is repeated at twice the speed, an effect known as "double time."

Diminution of note values

In mensural notation, diminution of the duration of note shapes is the most common function of coloration. Diminution is most often by one-third of the note-value, so that three colored notes fit into the time of two uncolored notes of the same shape; it is thus often found in notation of triplet or hemiola figures.[8][9]

Diminution may also be achieved by a sign of proportion. Thus a sign such as 3
2 is in proportional notation not a modern time signature, but a proportional signature indicating diminutio sesquialtera, that is, that after the sign each three notes of the basic note value integer valor occupy the time of two such notes elsewhere in the piece, either previously in the same voice, or simultaneously in another voice.[8]

Diminution of intervals

A diminished interval is an interval obtained from a minor interval or perfect interval by narrowing it by a chromatic semitone, meaning that the interval is narrowed by a semitone, but the staff positions are not changed (only an accidental is changed); the process may occasionally be referred to as diminution For example, a diminished fifth is a chromatic semitone narrower than the perfect fifth: starting with the interval from C to G, which is a perfect fifth, seven semitones wide, both the intervals from C to G♭, and from C♯ to G are diminished fifths, spanning six semitones, but the same staff lines. By contrast, the interval from D♭ to G is not a diminished fifth (it is an augmented fourth): even though it is six semitones wide, it spans four staff positions, and is thus a fourth, not a fifth; it is a diatonic semitone narrower than a perfect fifth. The standard abbreviations for diminished intervals are dX, such that a diminished third = d3.[10] The diminished fifth (d5) is the only diminished interval that appears in diatonic scales (in C major it occurs between B and F).

Diminished intervals on C
Diminished second Diminished third Diminished fourth Diminished fifth Diminished sixth Diminished seventh Diminished octave
PlayⓘPlayⓘPlayⓘPlayⓘPlayⓘPlayⓘPlayⓘ

a diminished unison is unthinkable, and the diminished 2d [sic] and 9th are of no practical use:...

— Foote[11]

In the theory of harmony it is known that a diminished interval needs to be resolved inwards, and an augmented interval outwards.

— Maria Renold (2004), p.15.[12]

Augmented intervals have a rather over-tense quality, while diminished intervals are experienced as rather cramped. Therefore, one may call the former luciferic in tendency and the latter ahrimanic.

— Renold (2004), p.16

If a perfect or major interval is made one-half step larger (without changing its interval number) it becomes augmented. If a perfect or minor interval is made one-half step smaller (without changing its interval number) it becomes diminished.

— Benward & Saker (2003), p.54.[10]

Most nonharmonic tones are dissonant and create intervals of a second, fourth, or seventh. Diminished or augmented intervals are also considered dissonant.

— Benward & Saker (2003), p.92.[13]

Diminished chords

Diminished triad on C playⓘ.

A diminished triad consists of two superposed minor thirds, and thus contains a diminished fifth. In classical repertoire the usual symbol is the degree, °, as in vii°. In lead sheets and popular music books it is usually written Cdim or C°.

Diminished seventh chord on C Playⓘ.

A diminished seventh chord consists of three superposed minor thirds, and thus has all successive notes a minor third apart; it contains two diminished fifths. In jazz theory, a diminished seventh chord has four available tensions, each a major ninth above the chord tones, and thus forming a diminished seventh chord a whole tone (or major ninth) above the root chord. Because any chord tone of the diminished seventh can be heard as the root, the tensions are not numbered as ninth, eleventh and so on. The usual notation is Cdim7 or C°7, but some lead sheets or popular music books may omit the 7.

Half-diminished seventh chord on C (Playⓘ).

A diminished triad with a minor seventh is a half-diminished chord, usually notated either Cm7(♭5) or Cø7. A diminished triad played over a root a major third away creates a Dominant 7th chord, notated C7, with a C Major triad on the bottom, and an E° from the chord third of C (C E G B♭). A minor third below would give a fully diminished 7th chord which is made entirely of minor thirds that evenly divide an octave. This even division of the octave leaves us with only three unique diminished 7th chords: C E♭ G♭ Bdouble flat, C♯ E G B♭, and D F A♭ C♭, as all other diminished 7th chords are inversions of one of those three.

Diminished chords with sheet music and tab.

Diminished scales

Octatonic scales on C Playⓘ.

Several scales may be referred to as diminished. One of the more common is the Octatonic scale constructed from C°7 and its tensions (transposed into the same octave), which has alternating tone and semitone intervals.

Half diminished scale on C Playⓘ.

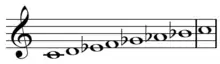
See also

References

  1. ↑ Greer Garden, Robert Donington (2001). Diminution. Grove Music Online. Oxford Music Online. Accessed August 2011. doi:10.1093/gmo/9781561592630.article.42071. (subscription required).
  2. ↑ Robert Donington (1989). The Interpretation of Early Music (new revised edition). London: Faber and Faber. pp. 152–188. ISBN 0571150403.
  3. ↑ Giovanni Luca Conforto, Giancarlo Rostirolla (editor) (1986). Breve et facile maniera d'essercitarsi a far passaggi, Roma 1593 (in Italian). Roma: Società Italiana del Flauto Dolce.
  4. ↑ Schenker, Heinrich (1979). Free Composition. Translated by Ernst Oster. New York, London: Longman. pp. 96, § 252.
  5. ↑ Schenker, Heinrich (1979). Free Composition. Translated by Ernst Oster. New York, London: Longman. pp. 98, § 253.
  6. ↑ Schenker, Heinrich (1908) [1904]. Ein Beitrag zur Ornamentik als Einführung zu Ph. Em. Bach's Klavierwerken. Wien, Leipzig: Universal Edition.
  7. ↑ Jeppesen, Knud. Counterpoint: The Polyphonic Vocal Style of the Sixteenth Century. trans. Glen Haydon. New York: Dover Publications. 1992. p. 235 Jeppesen, Knud (January 1992). Counterpoint: The Polyphonic Vocal Style of the Sixteenth Century. Courier Corporation. ISBN 978-0-486-27036-4.
  8. 1 2 Roger Bowers (2001). Proportional notation. Grove Music Online. Oxford Music Online. Accessed August 2011. doi:10.1093/gmo/9781561592630.article.22424. (subscription required).
  9. ↑ Robert Donington, Peter Wright (2001). Coloration. Grove Music Online. Oxford Music Online. Accessed August 2011. doi:10.1093/gmo/9781561592630.article.06153. (subscription required).
  10. 1 2 Benward & Saker (2003). Music: In Theory and Practice, Vol. I, p.54. ISBN 978-0-07-294262-0.
  11. ↑ Arthur Foote, Walter Raymond Spalding (1905). Modern Harmony in its Theory and Practice, p.5. Arthur P. Schmidt.
  12. ↑ Renold, Maria (2004). Intervals, scales, tones and the concert pitch, p.15. ISBN 1-902636-46-5.
  13. ↑ Benward & Saker (2003), p.92. Benward & Saker (2009). Music: In Theory and Practice, Vol. II, p.36. ISBN 978-0-07-310188-0.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.