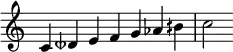
The double harmonic major scale[1] is a musical scale with a flattened second and sixth degree. This is also known as Mayamalavagowla, Bhairav Raga, Byzantine scale, Arabic (Hijaz Kar),[1][2] and Gypsy major.[3] It can be likened to a gypsy scale because of the diminished step between the 1st and 2nd degrees. Arabic scale may also refer to any Arabic mode, the simplest of which, however, to Westerners, resembles the double harmonic major scale.[4]
Details
The sequence of steps comprising the double harmonic scale is :
- half, augmented second, half, whole, half, augmented second, half
Or, in relation to the tonic note
- minor second, major third, perfect fourth and fifth, minor sixth, major seventh, octave
However, this scale is commonly represented with the first and last half step each being represented with quarter tones:
The non-quarter tone form is identical, in terms of notes, to the North Indian Thaat named Bhairav and the South Indian (Carnatic) Melakarta named Mayamalavagowla.
The double harmonic scale is arrived at by either:
- lowering both the second and sixth of the Ionian mode by a semitone.
- lowering the second note and raising the third note of the harmonic minor scale by one semitone.
- raising the seventh of the Phrygian dominant scale (a mode of the harmonic minor scale) by a semitone. The Phrygian dominant in turn is produced by raising the third of the diatonic Phrygian mode (a mode of the major scale) by a semitone.
- raising the third of the neapolitan minor scale by a semitone.
- lowering the second note of the harmonic major scale by a semitone.
- combining the lower half of the Phrygian dominant scale with the upper half of harmonic minor.[1]
It is referred to as the "double harmonic" scale because it contains two harmonic tetrads featuring augmented seconds. By contrast, both the harmonic major and harmonic minor scales contain only one augmented second, located between their sixth and seventh degrees.
The scale contains a built-in tritone substitution, a dominant seventh chord a half step above the root, with strong harmonic movement towards the tonic chord.
The double harmonic scale is not commonly used in classical music from Western culture, as it does not closely follow any of the basic musical modes, nor is it easily derived from them. It also does not easily fit into common Western chord progressions such as the authentic cadence. This is because it is mostly used as a modal scale, not intended for much movement through chord progressions.
The Arabic scale (in the key of E) was used in Nikolas Roubanis's "Misirlou", and in the Bacchanale from the opera Samson and Delilah by Saint-Saëns. Claude Debussy used the scale in "Soirée dans Grenade", "La Puerta del Vino", and "Sérénade interrompue" to evoke Spanish flamenco music or Moorish heritage.[5] In popular music, Ritchie Blackmore of Deep Purple and Rainbow used the scale in pieces such as "Gates of Babylon" and "Stargazer". The Miles Davis jazz standard "Nardis" also makes use of the double harmonic.. Opeth used this scale in their song "Bleak" from the album Blackwater Park. Megadeth use the scale in a guitar solo from their song "The Threat Is Real" from their 2015 album Dystopia. It is also used by Hans Zimmer in his score for Dune.
Symmetry and balance
The double harmonic scale features radial symmetry, or symmetry around its root, or center note. Breaking up the three note chromaticism and removing this symmetry by sharpening the 2nd or flattening the 7th note respectively by one semitone yields the harmonic major and Phrygian Dominant mode of the harmonic minor scales respectively, each of which, unlike the double harmonic minor scale, has a full diminished chord backbone.
This scale (and its modes like the Hungarian minor scale) is the only seven-note scale (in 12-tone equal temperament) that is perfectly balanced; this means that when its pitches are represented as points on a circle (whose full circumference represents an octave), their average position (or "centre of mass") is the centre of the circle.[6]
Tetrads
The main chords of the double harmonic major are:
I7M bII7M iii6 iv7M V7(b5) bVI7M(#5) viisus2add13(b5)
There are other possibilities of tetrad:
I7M(#5) bII7 bii7M bii7 bii7(b5) III6 iv° V6(b5) bvi°
Modes
Like all heptatonic (seven-pitch) scales, the double harmonic scale has a mode for each of its individual scale degrees. The most commonly known of these modes is the 4th mode, the Hungarian minor scale, most similar to the harmonic minor scale with a raised 4th degree. The modes are as follows:[7]
Mode Name of scale Degrees 1 Double harmonic major 1 ♭2 3 4 5 ♭6 7 8 2 Lydian ♯2 ♯6 1 ♯2 3 ♯4 5 ♯6 7 8 3 Ultraphrygian 1 ♭2 ♭3 ♭4 5 ♭6 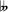 7
78 4 Hungarian/Gypsy minor 1 2 ♭3 ♯4 5 ♭6 7 8 5 Oriental 1 ♭2 3 4 ♭5 6 ♭7 8 6 Ionian ♯2 ♯5 1 ♯2 3 4 ♯5 6 7 8 7 Locrian 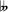 3
3 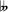 7
71 ♭2 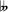 3
34 ♭5 ♭6 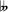 7
78
Related scales
Some of the closest existing scales to the double harmonic major scale are the Phrygian dominant scale, the fifth mode of the harmonic minor scale, as they are alike save for the Phrygian dominant's flattened seventh degree. The harmonic major scale (also known as major flat 6 and Ionian flat 6) is identical to the standard major scale aside from the sixth scale degree being flattened by a semitone, differing from the double harmonic major in having a natural second degree.
See also
References
- 1 2 3 Stetina, Troy (1999). The Ultimate Scale Book, p. 59. ISBN 0-7935-9788-9.
- ↑ Christiansen, Mike (2003). Mel Bay Complete Guitar Scale Dictionary, p. 43. ISBN 0-7866-6994-2.
- ↑ Jonathan Bellman, The "Style hongrois" in the Music of Western Europe (Boston: Northeastern University Press Archived 2011-01-15 at the Wayback Machine, 1993): 120. ISBN 1-55553-169-5.
- ↑ "R. G. Kiesewetter's 'Die Musik der Araber': A Pioneering Ethnomusicological Study of Arabic Writings on Music", p. 12. Philip V. Bohlman. Asian Music, vol. 18, no. 1. (Autumn–Winter, 1986), pp. 164–196.
- ↑ Elie Robert Schmitz, Virgil Thomson (1966). The Piano Works of Claude Debussy, p. 28. ISBN 0-486-21567-9.
- ↑ Milne, A. J., Bulger, D., Herff, S. A. Sethares, W. A. "Perfect balance: A novel principle for the construction of musical scales and meters", Mathematics and Computation in Music (Lecture Notes in Computer Science, vol. 9110, pp. 97–108) Heidelberg: Springer. ISBN 978-3-319-20602-8
- ↑ Patrice, "Acheter une guitare électrique – Zoom pour ne pas se tromper Archived June 18, 2015, at the Wayback Machine" 23 May 2016 (accessed 9 October 2016).
Further reading
- Hewitt, Michael. 2013. Musical Scales of the World. The Note Tree. ISBN 978-0957547001.