Comparison of intervals near or enharmonic with the unison

In music, two written notes have enharmonic equivalence if they produce the same pitch but are notated differently. This relation extends to pitch classes, chords, and key signatures. The term derives from Latin enharmonicus, in turn from Late Latin enarmonius, from Ancient Greek ἐναρμόνιος (enarmónios), from ἐν ('in') and ἁρμονία ('harmony').

Definition

In twelve-tone equal temperament tuning (the predominant system of musical tuning in Western music), the notes C♯ and D♭ are the same pitch and so are considered enharmonic or enharmonically equivalent. While they are identical in pitch, that pitch may be notated differently depending on its role in harmony. Arbitrary amounts of accidentals can produce further enharmonic equivalents, such as Bdouble sharp (B-double sharp), although these are used less frequently. "Enharmonic intervals are intervals with the same sound that are spelled differently... [resulting], of course, from enharmonic tones."[1]

Prior to this modern meaning, "enharmonic" referred to notes that were very close in pitch—closer than the smallest step of a diatonic scale—but not identical in pitch. One such example is G♯, which is not the same note and sound as A♭ in many temperaments of more than twelve tones,[2] as in an enharmonic scale. "Enharmonic equivalence is peculiar to post-tonal theory."[3] "Much music since at least the 18th century, however, exploits enharmonic equivalence for purposes of modulation and this requires that enharmonic equivalents in fact be equivalent."[4]

{ \magnifyStaff #5/4 \omit Score.TimeSignature \clef F \time 2/1 fis2 s ges s }
The notes F♯ and G♭ are enharmonic equivalents.
\relative c' { \magnifyStaff #5/4 \omit Score.TimeSignature \time 2/1 eis2 s fes s}
E♯ and F♭, however, are not enharmonic equivalents, because E♯ is enharmonic with F♮.
\relative c' { \magnifyStaff #5/4 \omit Score.TimeSignature \clef C \time 2/1 gisis2 s beses s}
Gdouble sharp and Bdouble flat are enharmonic equivalents, both the same as A♮.

Some key signatures have an enharmonic equivalent that represents a scale identical in sound but spelled differently. The number of sharps and flats of two enharmonically equivalent keys sum to twelve. For example, the key of B major, with five sharps, is enharmonically equivalent to the key of C♭ major with seven flats (five (sharps) + seven (flats) = 12). Keys with more than seven sharps or flats are considered theoretical keys. There are three major pairs and three minor pairs of enharmonically equivalent keys: B major/C♭ major, G♯ minor/A♭ minor, F♯ major/G♭ major, D♯ minor/E♭ minor, C♯ major/D♭ major and A♯ minor/B♭ minor. Works composed in keys that require double sharps or double flats are rare.

Enharmonic equivalents can be used to improve the readability of music, as when a sequence of notes is more easily read using sharps or flats. This may also reduce the number of accidentals required. Thus, in the key of B♭ major, the sequence B♭-B♮-B♭ may be easier to read using C♭ instead of B♮.

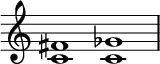
\relative c' { \magnifyStaff #5/4 \omit Score.TimeSignature \time 2/1 <c fis>1 <c ges'>}
Enharmonic tritones: augmented 4th = diminished 5th on C.

For example, the intervals of a minor sixth on C, on B♯, and an augmented fifth on C are all enharmonic intervals Playⓘ. The most common enharmonic intervals are the augmented fourth and diminished fifth, or tritone, for example C–F♯ = C–G♭.[5] "Enharmonic intervals are intervals with the same sound that are spelled differently... [resulting], of course, from enharmonic tones."[6]


Examples in practice

The melody of "All the Things You Are" (by Jerome Kern) has a G sharp at the end of the bridge section which, as the harmony changes, is then notated as an A flat (the first note of the returning "A" section).[7][8]

Beethoven's Piano Sonata in E Minor, Op. 90, contains a passage where the lowest note, B-flat, becomes an A-sharp, altering its musical function. The first two bars of the following passage unfold a descending B-flat major scale. According to Wilfrid Mellers, the B-flats here "turn out to be a pun, since they change enharmonically into A-sharps, part of a dominant ninth leading to B minor."[9]

Beethoven Sonata in E Minor Op. 90, first movement, bars 37–45

Chopin's Prelude No. 15, known as the "Raindrop Prelude", features a pedal point on the note A-flat throughout its opening section.

Chopin Prelude No. 15, opening

"The repeated A-flats ... become enharmonically changed into G-sharps in the middle section of this Prelude, and take on a brooding, ominous character."[10]

Chopin Prelude No. 15, bars 28–29

The concluding passage of the slow movement of Schubert's final piano sonata in B-flat (D960) contains a dramatic enharmonic change. In bars 102–3, the B-sharp transforms into C natural as part of a progression where a G sharp chord (the dominant chord of C sharp minor) "melts with breathtaking effect into a C major chord."[11]

\relative c'' { \magnifyStaff #5/4 \omit Score.TimeSignature \set doubleSlurs = ##t <bis dis gis>1 (<c e g!>)}
G-sharp to C progression.
Schubert Piano Sonata D960 second movement, bars 98–106

Tuning enharmonics

The modern musical use of the word enharmonic to mean identical tones is correct only in equal temperament, where the octave is divided into 12 equal semitones. In other tuning systems these pairs of notes do not indicate an identical pitch.[12]

Pythagorean

In Pythagorean tuning, all pitches are generated from a series of justly tuned perfect fifths, each with a frequency ratio of 3 to 2. If the first note in the series is an A♭, the thirteenth note in the series, G♯ is higher than the seventh octave (octave = ratio of 1 to 2, seven octaves is 1 to 27 = 128) of the A♭ by a small interval called a Pythagorean comma. This interval is expressed mathematically as:

Meantone

In quarter-comma meantone, there will be a discrepancy between, for example, G♯ and A♭. If middle C's frequency is x, the next highest C has a frequency of 2x. The quarter-comma meantone has perfectly tuned ("just") major thirds, which means major thirds with a frequency ratio of exactly 4 to 5. To form a just major third with the C above it, A♭ and the C above it must be in the ratio 4 to 5, so A♭ needs to have the frequency

To form a just major third above E, however, G♯ needs to form the ratio 5 to 4 with E, which, in turn, needs to form the ratio 5 to 4 with C, making the frequency of G♯

This leads to G♯ and A♭ being different pitches; G♯ is, in fact 41 cents (41% of a semitone) lower in pitch. The difference is the interval called the enharmonic diesis, or a frequency ratio of 128/125. On a piano tuned in equal temperament, both G♯ and A♭ are played by striking the same key, so both have a frequency

Such small differences in pitch can escape notice when presented as melodic intervals. However, when they are sounded as chords, the difference between meantone intonation and equal-tempered intonation can be quite noticeable.

Enharmonically equivalent pitches can be referred to with a single name in many situations, such as the numbers of integer notation used in serialism and musical set theory and employed by the MIDI interface.

Enharmonic genus

In ancient Greek music the enharmonic was one of the three Greek genera in music in which the tetrachords are divided (descending) as a ditone plus two microtones. The ditone can be anywhere from 16/13 to 9/7 (3.55 to 4.35 semitones) and the microtones can be anything smaller than 1 semitone.[13] Some examples of enharmonic genera are

  1. 1/1 36/35 16/15 4/3
  2. 1/1 28/27 16/15 4/3
  3. 1/1 64/63 28/27 4/3
  4. 1/1 49/48 28/27 4/3
  5. 1/1 25/24 13/12 4/3

Enharmonic key

Enharmonic key, like enharmonic, refers to a key that has a different key name but produces the same sound. Each tonic note corresponding to the enharmonic key relationship has an enharmonic relationship with each other.

The following scales are each in the Enharmonic key.

Major

D flat major - C sharp major
G flat major - F sharp major
C flat major - B major

Minor

B flat minor - A sharp minor
E flat minor - D sharp minor
A flat minor - G sharp minor

Theoretical

F flat major - (E major)
G sharp major - (A flat major)
D flat minor - (C sharp minor)
E sharp minor - (F minor)

The above is based on 12 TET, and in other pitches, the sound may be completely different from the above.

See also

References

  1. ↑ Benward, Bruce; Saker, Marilyn (2003). Music in Theory and Practice. Vol. I. p. 54. ISBN 978-0-07-294262-0.
  2. ↑ Elson, Louis Charles (1905). Elson's Music Dictionary. O. Ditson Company. p. 100. The relation existing between two chromatics, when, by the elevation of one and depression of the other, they are united into one.
  3. ↑ Randel, Don Michael, ed. (2003). "Set theory". The Harvard Dictionary of Music (4th ed.). Cambridge, MA: Belknap Press of Harvard University Press. p. 776. ISBN 978-0-674-01163-2.
  4. ↑ Randel, Don Michael, ed. (2003). "Enharmonic". The Harvard Dictionary of Music (4th ed.). Cambridge, MA: Belknap Press of Harvard University Press. p. 295. ISBN 978-0-674-01163-2.
  5. ↑ Benward, Bruce; Saker, Marilyn (2003). Music in Theory and Practice. Vol. I. p. 7 & 360. ISBN 978-0-07-294262-0.
  6. ↑ Benward, Bruce; Saker, Marilyn (2003). Music in Theory and Practice. Vol. I. p. 54. ISBN 978-0-07-294262-0.
  7. ↑ Kern, J. and Hammerstein, O. (1939, bars 23-25) "All the things you are", New York, T. B. Harms Co.
  8. ↑ Archived at Ghostarchive and the Wayback Machine: "Ella Fitzgerald - All The Things You Are (with lyrics)". YouTube.
  9. ↑ Mellers, W. (1983, p.132) Beethoven and the Voice of God. London, Faber.
  10. ↑ Walker, A. (2018, p. 383), Fryderyk Chopin, a Life and Times. London, Faber.
  11. ↑ Newbould, B., (1997, p.336) Schubert, the Music and the Man, London, Gollancz.
  12. ↑ Rushton, Julian (2001). "Enharmonic". In Sadie, Stanley; Tyrrell, John (eds.). The New Grove Dictionary of Music and Musicians (2nd ed.). London: Macmillan Publishers. ISBN 0-19-517067-9.
  13. ↑ Barbera, C. André (1977). "Arithmetic and Geometric Divisions of the Tetrachord". Journal of Music Theory. 21 (2): 294–323. doi:10.2307/843492. JSTOR 843492.

Further reading

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.