In mathematics, Faulhaber's formula, named after the early 17th century mathematician Johann Faulhaber, expresses the sum of the p-th powers of the first n positive integers

$${\displaystyle \sum _{k=1}^{n}k^{p}=1^{p}+2^{p}+3^{p}+\cdots +n^{p}}$$

as a polynomial in n. In modern notation, Faulhaber's formula is

$${\displaystyle \sum _{k=1}^{n}k^{p}={\frac {1}{p+1}}\sum _{r=0}^{p}{\binom {p+1}{r}}B_{r}n^{p-r+1}.}$$

Here, ${\textstyle {\binom {p+1}{r}}}$ is the binomial coefficient "p + 1 choose r", and the B_j are the Bernoulli numbers with the convention that ${\textstyle B_{1}=+{\frac {1}{2}}}$.

The result: Faulhaber's formula

Faulhaber's formula concerns expressing the sum of the p-th powers of the first n positive integers

$${\displaystyle \sum _{k=1}^{n}k^{p}=1^{p}+2^{p}+3^{p}+\cdots +n^{p}}$$

as a (p + 1)th-degree polynomial function of n.

The first few examples are well known. For p = 0, we have

$${\displaystyle \sum _{k=1}^{n}k^{0}=\sum _{k=1}^{n}1=n.}$$

For p = 1, we have the triangular numbers

$${\displaystyle \sum _{k=1}^{n}k^{1}=\sum _{k=1}^{n}k={\frac {n(n+1)}{2}}={\frac {1}{2}}(n^{2}+n).}$$

For p = 2, we have the square pyramidal numbers

$${\displaystyle \sum _{k=1}^{n}k^{2}={\frac {n(n+1)(2n+1)}{6}}={\frac {1}{3}}(n^{3}+{\tfrac {3}{2}}n^{2}+{\tfrac {1}{2}}n).}$$

The coefficients of Faulhaber's formula in its general form involve the Bernoulli numbers B_j. The Bernoulli numbers begin

$${\displaystyle {\begin{aligned}B_{0}&=1&B_{1}&={\tfrac {1}{2}}&B_{2}&={\tfrac {1}{6}}&B_{3}&=0\\B_{4}&=-{\tfrac {1}{30}}&B_{5}&=0&B_{6}&={\tfrac {1}{42}}&B_{7}&=0,\end{aligned}}}$$

where here we use the convention that ${\textstyle B_{1}=+{\frac {1}{2}}}$. The Bernoulli numbers have various definitions (see Bernoulli number#Definitions), such as that they are the coefficients of the exponential generating function

$${\displaystyle {\frac {t}{1-\mathrm {e} ^{-t}}}={\frac {t}{2}}\left(\operatorname {coth} {\frac {t}{2}}+1\right)=\sum _{k=0}^{\infty }B_{k}{\frac {t^{k}}{k!}}.}$$

Then Faulhaber's formula is that

$${\displaystyle \sum _{k=1}^{n}k^{p}={\frac {1}{p+1}}\sum _{k=0}^{p}{\binom {p+1}{k}}B_{k}n^{p-k+1}.}$$

Here, the B_j are the Bernoulli numbers as above, and

$${\displaystyle {\binom {p+1}{k}}={\frac {(p+1)!}{(p+1-k)!\,k!}}={\frac {(p+1)p(p-1)\cdots (p-k+3)(p-k+2)}{k(k-1)(k-2)\cdots 2\cdot 1}}}$$

is the binomial coefficient "p + 1 choose k".

Examples

So, for example, one has for p = 4,

$${\displaystyle {\begin{aligned}1^{4}+2^{4}+3^{4}+\cdots +n^{4}&={\frac {1}{5}}\sum _{j=0}^{4}{5 \choose j}B_{j}n^{5-j}\\&={\frac {1}{5}}\left(B_{0}n^{5}+5B_{1}n^{4}+10B_{2}n^{3}+10B_{3}n^{2}+5B_{4}n\right)\\&={\frac {1}{5}}\left(n^{5}+{\tfrac {5}{2}}n^{4}+{\tfrac {5}{3}}n^{3}-{\tfrac {1}{6}}n\right).\end{aligned}}}$$

The first seven examples of Faulhaber's formula are

$${\displaystyle {\begin{aligned}\sum _{k=1}^{n}k^{0}&={\frac {1}{1}}\,{\big (}n{\big )}\\\sum _{k=1}^{n}k^{1}&={\frac {1}{2}}\,{\big (}n^{2}+{\tfrac {2}{2}}n{\big )}\\\sum _{k=1}^{n}k^{2}&={\frac {1}{3}}\,{\big (}n^{3}+{\tfrac {3}{2}}n^{2}+{\tfrac {3}{6}}n{\big )}\\\sum _{k=1}^{n}k^{3}&={\frac {1}{4}}\,{\big (}n^{4}+{\tfrac {4}{2}}n^{3}+{\tfrac {6}{6}}n^{2}+0n{\big )}\\\sum _{k=1}^{n}k^{4}&={\frac {1}{5}}\,{\big (}n^{5}+{\tfrac {5}{2}}n^{4}+{\tfrac {10}{6}}n^{3}+0n^{2}-{\tfrac {5}{30}}n{\big )}\\\sum _{k=1}^{n}k^{5}&={\frac {1}{6}}\,{\big (}n^{6}+{\tfrac {6}{2}}n^{5}+{\tfrac {15}{6}}n^{4}+0n^{3}-{\tfrac {15}{30}}n^{2}+0n{\big )}\\\sum _{k=1}^{n}k^{6}&={\frac {1}{7}}\,{\big (}n^{7}+{\tfrac {7}{2}}n^{6}+{\tfrac {21}{6}}n^{5}+0n^{4}-{\tfrac {35}{30}}n^{3}+0n^{2}+{\tfrac {7}{42}}n{\big )}.\end{aligned}}}$$

History

Faulhaber's formula is also called Bernoulli's formula. Faulhaber did not know the properties of the coefficients later discovered by Bernoulli. Rather, he knew at least the first 17 cases, as well as the existence of the Faulhaber polynomials for odd powers described below.^[1]

Jakob Bernoulli's Summae Potestatum, Ars Conjectandi, 1713

In 1713, Jacob Bernoulli published under the title Summae Potestatum an expression of the sum of the p powers of the n first integers as a (p + 1)th-degree polynomial function of n, with coefficients involving numbers B_j, now called Bernoulli numbers:

${\displaystyle \sum _{k=1}^{n}k^{p}={\frac {n^{p+1}}{p+1}}+{\frac {1}{2}}n^{p}+{1 \over p+1}\sum _{j=2}^{p}{p+1 \choose j}B_{j}n^{p+1-j}.}$

Introducing also the first two Bernoulli numbers (which Bernoulli did not), the previous formula becomes

$${\displaystyle \sum _{k=1}^{n}k^{p}={1 \over p+1}\sum _{j=0}^{p}{p+1 \choose j}B_{j}n^{p+1-j},}$$

using the Bernoulli number of the second kind for which ${\textstyle B_{1}={\frac {1}{2}}}$, or

$${\displaystyle \sum _{k=1}^{n}k^{p}={1 \over p+1}\sum _{j=0}^{p}(-1)^{j}{p+1 \choose j}B_{j}^{-}n^{p+1-j},}$$

using the Bernoulli number of the first kind for which ${\textstyle B_{1}^{-}=-{\frac {1}{2}}.}$

Faulhaber himself did not know the formula in this form, but only computed the first seventeen polynomials; the general form was established with the discovery of the Bernoulli numbers.

A rigorous proof of these formulas and Faulhaber's assertion that such formulas would exist for all odd powers took until Carl Jacobi (1834), two centuries later.

Proof with exponential generating function

Let

$${\displaystyle S_{p}(n)=\sum _{k=1}^{n}k^{p},}$$

denote the sum under consideration for integer ${\displaystyle p\geq 0.}$

Define the following exponential generating function with (initially) indeterminate ${\displaystyle z}$

$${\displaystyle G(z,n)=\sum _{p=0}^{\infty }S_{p}(n){\frac {1}{p!}}z^{p}.}$$

We find

$${\displaystyle {\begin{aligned}G(z,n)=&\sum _{p=0}^{\infty }\sum _{k=1}^{n}{\frac {1}{p!}}(kz)^{p}=\sum _{k=1}^{n}e^{kz}=e^{z}\cdot {\frac {1-e^{nz}}{1-e^{z}}},\\=&{\frac {1-e^{nz}}{e^{-z}-1}}.\end{aligned}}}$$

This is an entire function in ${\displaystyle z}$ so that ${\displaystyle z}$ can be taken to be any complex number.

We next recall the exponential generating function for the Bernoulli polynomials ${\displaystyle B_{j}(x)}$

$${\displaystyle {\frac {ze^{zx}}{e^{z}-1}}=\sum _{j=0}^{\infty }B_{j}(x){\frac {z^{j}}{j!}},}$$

where ${\displaystyle B_{j}=B_{j}(0)}$ denotes the Bernoulli number with the convention ${\displaystyle B_{1}=-{\frac {1}{2}}}$. This may be converted to a generating function with the convention ${\displaystyle B_{1}^{+}={\frac {1}{2}}}$ by the addition of ${\displaystyle j}$ to the coefficient of ${\displaystyle x^{j-1}}$ in each ${\displaystyle B_{j}(x)}$ (${\displaystyle B_{0}}$ does not need to be changed):

$${\displaystyle {\begin{aligned}\sum _{j=0}^{\infty }B_{j}^{+}(x){\frac {z^{j}}{j!}}=&{\frac {ze^{zx}}{e^{z}-1}}+\sum _{j=1}^{\infty }jx^{j-1}{\frac {z^{j}}{j!}}\\=&{\frac {ze^{zx}}{e^{z}-1}}+\sum _{j=1}^{\infty }x^{j-1}{\frac {z^{j}}{(j-1)!}}\\=&{\frac {ze^{zx}}{e^{z}-1}}+ze^{zx}\\=&{\frac {ze^{zx}+ze^{z}e^{zx}-ze^{zx}}{e^{z}-1}}\\=&{\frac {ze^{zx}}{1-e^{-z}}}\end{aligned}}}$$

It follows immediately that

$${\displaystyle S_{p}(n)={\frac {B_{p+1}^{+}(n)-B_{p+1}^{+}(0)}{p+1}}}$$

for all ${\displaystyle p}$.

Faulhaber polynomials

The term Faulhaber polynomials is used by some authors to refer to another polynomial sequence related to that given above.

Write

$${\displaystyle a=\sum _{k=1}^{n}k={\frac {n(n+1)}{2}}.}$$

Faulhaber observed that if p is odd then ${\textstyle \sum _{k=1}^{n}k^{p}}$ is a polynomial function of a.

Proof without words for p = 3 ^[2]

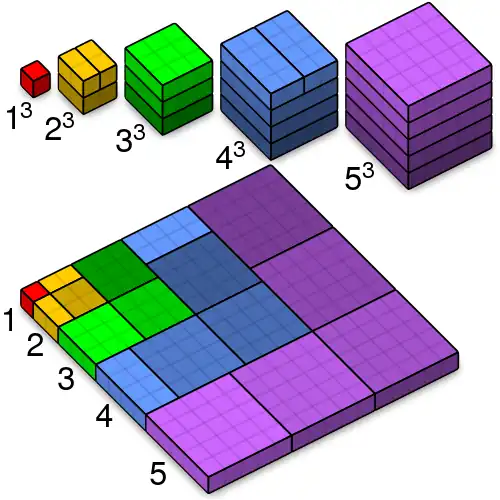
For p = 1, it is clear that

$${\displaystyle \sum _{k=1}^{n}k^{1}=\sum _{k=1}^{n}k={\frac {n(n+1)}{2}}=a.}$$

For p = 3, the result that

$${\displaystyle \sum _{k=1}^{n}k^{3}={\frac {n^{2}(n+1)^{2}}{4}}=a^{2}}$$

is known as Nicomachus's theorem.

Further, we have

$${\displaystyle {\begin{aligned}\sum _{k=1}^{n}k^{5}&={\frac {4a^{3}-a^{2}}{3}}\\\sum _{k=1}^{n}k^{7}&={\frac {6a^{4}-4a^{3}+a^{2}}{3}}\\\sum _{k=1}^{n}k^{9}&={\frac {16a^{5}-20a^{4}+12a^{3}-3a^{2}}{5}}\\\sum _{k=1}^{n}k^{11}&={\frac {16a^{6}-32a^{5}+34a^{4}-20a^{3}+5a^{2}}{3}}\end{aligned}}}$$

(see OEIS: A000537, OEIS: A000539, OEIS: A000541, OEIS: A007487, OEIS: A123095).

More generally,

$${\displaystyle \sum _{k=1}^{n}k^{2m+1}={\frac {1}{2^{2m+2}(2m+2)}}\sum _{q=0}^{m}{\binom {2m+2}{2q}}(2-2^{2q})~B_{2q}~\left[(8a+1)^{m+1-q}-1\right].}$$

Some authors call the polynomials in a on the right-hand sides of these identities Faulhaber polynomials. These polynomials are divisible by a² because the Bernoulli number B_j is 0 for odd j > 1.

Inversely, writing for simplicity ${\displaystyle s_{j}:=\sum _{k=1}^{n}k^{j}}$, we have

$${\displaystyle {\begin{aligned}4a^{3}&=3s_{5}+s_{3}\\8a^{4}&=4s_{7}+4s_{5}\\16a^{5}&=5s_{9}+10s_{7}+s_{5}\end{aligned}}}$$

and generally

$${\displaystyle 2^{m-1}a^{m}=\sum _{j>0}{\binom {m}{2j-1}}s_{2m-2j+1}.}$$

Faulhaber also knew that if a sum for an odd power is given by

$${\displaystyle \sum _{k=1}^{n}k^{2m+1}=c_{1}a^{2}+c_{2}a^{3}+\cdots +c_{m}a^{m+1}}$$

then the sum for the even power just below is given by

$${\displaystyle \sum _{k=1}^{n}k^{2m}={\frac {n+{\frac {1}{2}}}{2m+1}}(2c_{1}a+3c_{2}a^{2}+\cdots +(m+1)c_{m}a^{m}).}$$

Note that the polynomial in parentheses is the derivative of the polynomial above with respect to a.

Since a = n(n + 1)/2, these formulae show that for an odd power (greater than 1), the sum is a polynomial in n having factors n² and (n + 1)², while for an even power the polynomial has factors n, n + ½ and n + 1.

Expressing products of power sums as linear combinations of power sums

Products of two (and thus by iteration, several) power sums ${\displaystyle s_{j_{r}}:=\sum _{k=1}^{n}k^{j_{r}}}$ can be written as linear combinations of power sums with either all degrees even or all degrees odd, depending on the total degree of the product as a polynomial in ${\displaystyle n}$, e.g. ${\displaystyle 30s_{2}s_{4}=-s_{3}+15s_{5}+16s_{7}}$. Note that the sums of coefficients must be equal on both sides, as can be seen by putting ${\displaystyle n=1}$, which makes all the ${\displaystyle s_{j}}$ equal to 1. Some general formulae include:

$${\displaystyle {\begin{aligned}(m+1)s_{m}^{2}&=2\sum _{j=0}^{\lfloor {\frac {m}{2}}\rfloor }{\binom {m+1}{2j}}(2m+1-2j)B_{2j}s_{2m+1-2j}.\\m(m+1)s_{m}s_{m-1}&=m(m+1)B_{m}s_{m}+\sum _{j=0}^{\lfloor {\frac {m-1}{2}}\rfloor }{\binom {m+1}{2j}}(2m+1-2j)B_{2j}s_{2m-2j}.\\2^{m-1}s_{1}^{m}&=\sum _{j=1}^{\lfloor {\frac {m+1}{2}}\rfloor }{\binom {m}{2j-1}}s_{2m+1-2j}.\end{aligned}}}$$

Note that in the second formula, for even ${\displaystyle m}$ the term corresponding to ${\displaystyle j={\dfrac {m}{2}}}$ is different from the other terms in the sum, while for odd ${\displaystyle m}$, this additional term vanishes because of ${\displaystyle B_{m}=0}$.

Matrix form

Faulhaber's formula can also be written in a form using matrix multiplication.

Take the first seven examples

$${\displaystyle {\begin{aligned}\sum _{k=1}^{n}k^{0}&={\phantom {-}}1n\\\sum _{k=1}^{n}k^{1}&={\phantom {-}}{\tfrac {1}{2}}n+{\tfrac {1}{2}}n^{2}\\\sum _{k=1}^{n}k^{2}&={\phantom {-}}{\tfrac {1}{6}}n+{\tfrac {1}{2}}n^{2}+{\tfrac {1}{3}}n^{3}\\\sum _{k=1}^{n}k^{3}&={\phantom {-}}0n+{\tfrac {1}{4}}n^{2}+{\tfrac {1}{2}}n^{3}+{\tfrac {1}{4}}n^{4}\\\sum _{k=1}^{n}k^{4}&=-{\tfrac {1}{30}}n+0n^{2}+{\tfrac {1}{3}}n^{3}+{\tfrac {1}{2}}n^{4}+{\tfrac {1}{5}}n^{5}\\\sum _{k=1}^{n}k^{5}&={\phantom {-}}0n-{\tfrac {1}{12}}n^{2}+0n^{3}+{\tfrac {5}{12}}n^{4}+{\tfrac {1}{2}}n^{5}+{\tfrac {1}{6}}n^{6}\\\sum _{k=1}^{n}k^{6}&={\phantom {-}}{\tfrac {1}{42}}n+0n^{2}-{\tfrac {1}{6}}n^{3}+0n^{4}+{\tfrac {1}{2}}n^{5}+{\tfrac {1}{2}}n^{6}+{\tfrac {1}{7}}n^{7}.\end{aligned}}}$$

Writing these polynomials as a product between matrices gives

$${\displaystyle {\begin{pmatrix}\sum k^{0}\\\sum k^{1}\\\sum k^{2}\\\sum k^{3}\\\sum k^{4}\\\sum k^{5}\\\sum k^{6}\end{pmatrix}}=G_{7}{\begin{pmatrix}n\\n^{2}\\n^{3}\\n^{4}\\n^{5}\\n^{6}\\n^{7}\end{pmatrix}},}$$

where

$${\displaystyle G_{7}={\begin{pmatrix}1&0&0&0&0&0&0\\{1 \over 2}&{1 \over 2}&0&0&0&0&0\\{1 \over 6}&{1 \over 2}&{1 \over 3}&0&0&0&0\\0&{1 \over 4}&{1 \over 2}&{1 \over 4}&0&0&0\\-{1 \over 30}&0&{1 \over 3}&{1 \over 2}&{1 \over 5}&0&0\\0&-{1 \over 12}&0&{5 \over 12}&{1 \over 2}&{1 \over 6}&0\\{1 \over 42}&0&-{1 \over 6}&0&{1 \over 2}&{1 \over 2}&{1 \over 7}\end{pmatrix}}.}$$

Surprisingly, inverting the matrix of polynomial coefficients yields something more familiar:

$${\displaystyle G_{7}^{-1}={\begin{pmatrix}1&0&0&0&0&0&0\\-1&2&0&0&0&0&0\\1&-3&3&0&0&0&0\\-1&4&-6&4&0&0&0\\1&-5&10&-10&5&0&0\\-1&6&-15&20&-15&6&0\\1&-7&21&-35&35&-21&7\\\end{pmatrix}}={\overline {A}}_{7}}$$

In the inverted matrix, Pascal's triangle can be recognized, without the last element of each row, and with alternating signs.

Let ${\displaystyle A_{7}}$ be the matrix obtained from ${\displaystyle {\overline {A}}_{7}}$ by changing the signs of the entries in odd diagonals, that is by replacing ${\displaystyle a_{i,j}}$ by ${\displaystyle (-1)^{i+j}a_{i,j}}$, let ${\displaystyle {\overline {G}}_{7}}$ be the matrix obtained from ${\displaystyle G_{7}}$ with a similar transformation, then

$${\displaystyle A_{7}={\begin{pmatrix}1&0&0&0&0&0&0\\1&2&0&0&0&0&0\\1&3&3&0&0&0&0\\1&4&6&4&0&0&0\\1&5&10&10&5&0&0\\1&6&15&20&15&6&0\\1&7&21&35&35&21&7\\\end{pmatrix}}}$$

and

$${\displaystyle A_{7}^{-1}={\begin{pmatrix}1&0&0&0&0&0&0\\-{1 \over 2}&{1 \over 2}&0&0&0&0&0\\{1 \over 6}&-{1 \over 2}&{1 \over 3}&0&0&0&0\\0&{1 \over 4}&-{1 \over 2}&{1 \over 4}&0&0&0\\-{1 \over 30}&0&{1 \over 3}&-{1 \over 2}&{1 \over 5}&0&0\\0&-{1 \over 12}&0&{5 \over 12}&-{1 \over 2}&{1 \over 6}&0\\{1 \over 42}&0&-{1 \over 6}&0&{1 \over 2}&-{1 \over 2}&{1 \over 7}\end{pmatrix}}={\overline {G}}_{7}.}$$

Also

$${\displaystyle {\begin{pmatrix}\sum _{k=0}^{n-1}k^{0}\\\sum _{k=0}^{n-1}k^{1}\\\sum _{k=0}^{n-1}k^{2}\\\sum _{k=0}^{n-1}k^{3}\\\sum _{k=0}^{n-1}k^{4}\\\sum _{k=0}^{n-1}k^{5}\\\sum _{k=0}^{n-1}k^{6}\\\end{pmatrix}}={\overline {G}}_{7}{\begin{pmatrix}n\\n^{2}\\n^{3}\\n^{4}\\n^{5}\\n^{6}\\n^{7}\\\end{pmatrix}}}$$

This is because it is evident that ${\textstyle \sum _{k=1}^{n}k^{m}-\sum _{k=0}^{n-1}k^{m}=n^{m}}$ and that therefore polynomials of degree ${\displaystyle m+1}$ of the form ${\textstyle {\frac {1}{m+1}}n^{m+1}+{\frac {1}{2}}n^{m}+\cdots }$ subtracted the monomial difference ${\displaystyle n^{m}}$ they become ${\textstyle {\frac {1}{m+1}}n^{m+1}-{\frac {1}{2}}n^{m}+\cdots }$.

This is true for every order, that is, for each positive integer m, one has ${\displaystyle G_{m}^{-1}={\overline {A}}_{m}}$ and ${\displaystyle {\overline {G}}_{m}^{-1}=A_{m}.}$ Thus, it is possible to obtain the coefficients of the polynomials of the sums of powers of successive integers without resorting to the numbers of Bernoulli but by inverting the matrix easily obtained from the triangle of Pascal.^[3][4]

Variations

• Replacing ${\displaystyle k}$ with ${\displaystyle p-k}$, we find the alternative expression:
  $${\displaystyle \sum _{k=1}^{n}k^{p}=\sum _{k=0}^{p}{\frac {1}{k+1}}{p \choose k}B_{p-k}n^{k+1}.}$$

  
• Subtracting ${\displaystyle n^{p}}$ from both sides of the original formula and incrementing ${\displaystyle n}$ by ${\displaystyle 1}$, we get
  $${\displaystyle {\begin{aligned}\sum _{k=1}^{n}k^{p}&={\frac {1}{p+1}}\sum _{k=0}^{p}{\binom {p+1}{k}}(-1)^{k}B_{k}(n+1)^{p-k+1}\\&=\sum _{k=0}^{p}{\frac {1}{k+1}}{\binom {p}{k}}(-1)^{p-k}B_{p-k}(n+1)^{k+1},\end{aligned}}}$$

  

where ${\displaystyle (-1)^{k}B_{k}=B_{k}^{-}}$ can be interpreted as "negative" Bernoulli numbers with ${\displaystyle B_{1}^{-}=-{\tfrac {1}{2}}}$.

• We may also expand ${\displaystyle G(z,n)}$ in terms of the Bernoulli polynomials to find
  $${\displaystyle {\begin{aligned}G(z,n)&={\frac {e^{(n+1)z}}{e^{z}-1}}-{\frac {e^{z}}{e^{z}-1}}\\&=\sum _{j=0}^{\infty }\left(B_{j}(n+1)-(-1)^{j}B_{j}\right){\frac {z^{j-1}}{j!}},\end{aligned}}}$$

  
  which implies
  $${\displaystyle \sum _{k=1}^{n}k^{p}={\frac {1}{p+1}}\left(B_{p+1}(n+1)-(-1)^{p+1}B_{p+1}\right)={\frac {1}{p+1}}\left(B_{p+1}(n+1)-B_{p+1}(1)\right).}$$

  
  Since ${\displaystyle B_{n}=0}$ whenever ${\displaystyle n>1}$ is odd, the factor ${\displaystyle (-1)^{p+1}}$ may be removed when ${\displaystyle p>0}$.
• It can also be expressed in terms of Stirling numbers of the second kind and falling factorials as^[5]
  $${\displaystyle \sum _{k=0}^{n}k^{p}=\sum _{k=0}^{p}\left\{{p \atop k}\right\}{\frac {(n+1)_{k+1}}{k+1}},}$$

  
  $${\displaystyle \sum _{k=1}^{n}k^{p}=\sum _{k=1}^{p+1}\left\{{p+1 \atop k}\right\}{\frac {(n)_{k}}{k}}.}$$

  
  This is due to the definition of the Stirling numbers of the second kind as mononomials in terms of falling factorials, and the behaviour of falling factorials under the indefinite sum.

Interpreting the Stirling numbers of the second kind, ${\displaystyle \left\{{p+1 \atop k}\right\}}$, as the number of set partitions of ${\displaystyle \lbrack p+1\rbrack }$ into ${\displaystyle k}$ parts, the identity has a direct combinatorial proof since both sides count the number of functions ${\displaystyle f:\lbrack p+1\rbrack ->\lbrack n\rbrack }$ with ${\displaystyle f(1)}$ maximal. The index of summation on the left hand side represents ${\displaystyle k=f(1)}$, while the index on the right hand side is represents the number of elements in the image of f.

• There is also a similar (but somehow simpler) expression: using the idea of telescoping and the binomial theorem, one gets Pascal's identity:^[6]

$${\displaystyle {\begin{aligned}(n+1)^{k+1}-1&=\sum _{m=1}^{n}\left((m+1)^{k+1}-m^{k+1}\right)\\&=\sum _{p=0}^{k}{\binom {k+1}{p}}(1^{p}+2^{p}+\dots +n^{p}).\end{aligned}}}$$

This in particular yields the examples below – e.g., take k = 1 to get the first example. In a similar fashion we also find

$${\displaystyle {\begin{aligned}n^{k+1}=\sum _{m=1}^{n}\left(m^{k+1}-(m-1)^{k+1}\right)=\sum _{p=0}^{k}(-1)^{k+p}{\binom {k+1}{p}}(1^{p}+2^{p}+\dots +n^{p}).\end{aligned}}}$$

• Faulhaber's formula was generalized by Guo and Zeng to a q-analog.^[7]

Relationship to Riemann zeta function

Using ${\displaystyle B_{k}=-k\zeta (1-k)}$, one can write

$${\displaystyle \sum \limits _{k=1}^{n}k^{p}={\frac {n^{p+1}}{p+1}}-\sum \limits _{j=0}^{p-1}{p \choose j}\zeta (-j)n^{p-j}.}$$

If we consider the generating function ${\displaystyle G(z,n)}$ in the large ${\displaystyle n}$ limit for ${\displaystyle \Re (z)<0}$, then we find

$${\displaystyle \lim _{n\rightarrow \infty }G(z,n)={\frac {1}{e^{-z}-1}}=\sum _{j=0}^{\infty }(-1)^{j-1}B_{j}{\frac {z^{j-1}}{j!}}}$$

Heuristically, this suggests that

$${\displaystyle \sum _{k=1}^{\infty }k^{p}={\frac {(-1)^{p}B_{p+1}}{p+1}}.}$$

This result agrees with the value of the Riemann zeta function ${\textstyle \zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}}$ for negative integers ${\displaystyle s=-p<0}$ on appropriately analytically continuing ${\displaystyle \zeta (s)}$.

Umbral form

In the umbral calculus, one treats the Bernoulli numbers ${\textstyle B^{0}=1}$, ${\textstyle B^{1}={\frac {1}{2}}}$, ${\textstyle B^{2}={\frac {1}{6}}}$, … as if the index j in ${\textstyle B^{j}}$ were actually an exponent, and so as if the Bernoulli numbers were powers of some object B.

Using this notation, Faulhaber's formula can be written as

$${\displaystyle \sum _{k=1}^{n}k^{p}={\frac {1}{p+1}}{\big (}(B+n)^{p+1}-B^{p+1}{\big )}.}$$

Here, the expression on the right must be understood by expanding out to get terms ${\textstyle B^{j}}$ that can then be interpreted as the Bernoulli numbers. Specifically, using the binomial theorem, we get

$${\displaystyle {\begin{aligned}{\frac {1}{p+1}}{\big (}(B+n)^{p+1}-B^{p+1}{\big )}&={1 \over p+1}\left(\sum _{k=0}^{p+1}{\binom {p+1}{k}}B^{k}n^{p+1-k}-B^{p+1}\right)\\&={1 \over p+1}\sum _{k=0}^{p}{\binom {p+1}{j}}B^{k}n^{p+1-k}.\end{aligned}}}$$

A derivation of Faulhaber's formula using the umbral form is available in The Book of Numbers by John Horton Conway and Richard K. Guy.^[8]

Classically, this umbral form was considered as a notational convenience. In the modern umbral calculus, on the other hand, this is given a formal mathematical underpinning. One considers the linear functional T on the vector space of polynomials in a variable b given by ${\textstyle T(b^{j})=B_{j}.}$ Then one can say

$${\displaystyle {\begin{aligned}\sum _{k=1}^{n}k^{p}&={1 \over p+1}\sum _{j=0}^{p}{p+1 \choose j}B_{j}n^{p+1-j}\\&={1 \over p+1}\sum _{j=0}^{p}{p+1 \choose j}T(b^{j})n^{p+1-j}\\&={1 \over p+1}T\left(\sum _{j=0}^{p}{p+1 \choose j}b^{j}n^{p+1-j}\right)\\&=T\left({(b+n)^{p+1}-b^{p+1} \over p+1}\right).\end{aligned}}}$$

See also

• Polynomials calculating sums of powers of arithmetic progressions

Notes

External links

• Jacobi, Carl (1834). "De usu legitimo formulae summatoriae Maclaurinianae". Journal für die reine und angewandte Mathematik. Vol. 12. pp. 263–72.
• Weisstein, Eric W. "Faulhaber's formula". MathWorld.
• Johann Faulhaber (1631). Academia Algebrae - Darinnen die miraculosische Inventiones zu den höchsten Cossen weiters continuirt und profitiert werden. A very rare book, but Knuth has placed a photocopy in the Stanford library, call number QA154.8 F3 1631a f MATH. (online copy at Google Books)
• Beardon, A. F. (1996). "Sums of Powers of Integers" (PDF). American Mathematical Monthly. 103 (3): 201–213. doi:10.1080/00029890.1996.12004725. Retrieved 2011-10-23. (Winner of a Lester R. Ford Award)
• Schumacher, Raphael (2016). "An Extended Version of Faulhaber's Formula" (PDF). Journal of Integer Sequences. Vol. 19.

• Orosi, Greg (2018). "A Simple Derivation Of Faulhaber's Formula" (PDF). Applied Mathematics E-Notes. Vol. 18. pp. 124–126.
• A visual proof for the sum of squares and cubes.