A classical approach to solve the Hypergraph bipartitioning problem is an iterative heuristic by Charles Fiduccia and Robert Mattheyses.[1] This heuristic is commonly called the FM algorithm.
Introduction
FM algorithm is a linear time heuristic for improving network partitions. New features to K-L heuristic:
- Aims at reducing net-cut costs; the concept of cutsize is extended to hypergraphs.
- Only a single vertex is moved across the cut in a single move.
- Vertices are weighted.
- Can handle "unbalanced" partitions; a balance factor is introduced.
- A special data structure is used to select vertices to be moved across the cut to improve running time.
- Time complexity O(P), where P is the total # of terminals.
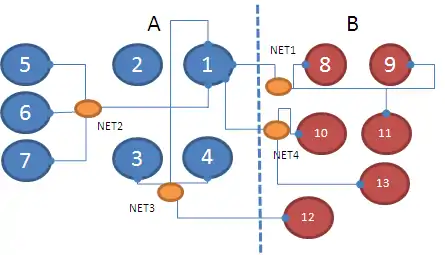
Example of FM
F–M heuristic: notation
Input: A hypergraph with a vertex (cell) set and a hyperedge (net) set
- n(i): # of cells in Net i; e.g., n(1) = 4
- s(i): size of Cell i
- p(i): # of pins of Cell i; e.g., p(1) = 4
- C: total # of cells; e.g., C = 13
- N: total # of nets; e.g., N = 4
- P: total # of pins; P = p(1) + … + p(C) = n(1) + … + n(N)
- Area ratio r, 0< r<1
Output: 2 partitions
- Cutsetsize is minimized
- |A|/(|A|+|B|) ≈ r
See also
References
- ↑ Fiduccia; Mattheyses (1982). "A Linear-Time Heuristic for Improving Network Partitions". 19th Design Automation Conference. pp. 175–181. doi:10.1109/DAC.1982.1585498. ISBN 0-89791-020-6. Retrieved 23 October 2013.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.