Magma (algebra)

In abstract algebra, a magma, binar,^[1] or, rarely, groupoid is a basic kind of algebraic structure. Specifically, a magma consists of a set equipped with a single binary operation that must be closed by definition. No other properties are imposed.

History and terminology

The term groupoid was introduced in 1927 by Heinrich Brandt describing his Brandt groupoid (translated from the German Gruppoid). The term was then appropriated by B. A. Hausmann and Øystein Ore (1937)^[2] in the sense (of a set with a binary operation) used in this article. In a couple of reviews of subsequent papers in Zentralblatt, Brandt strongly disagreed with this overloading of terminology. The Brandt groupoid is a groupoid in the sense used in category theory, but not in the sense used by Hausmann and Ore. Nevertheless, influential books in semigroup theory, including Clifford and Preston (1961) and Howie (1995) use groupoid in the sense of Hausmann and Ore. Hollings (2014) writes that the term groupoid is "perhaps most often used in modern mathematics" in the sense given to it in category theory.^[3]

According to Bergman and Hausknecht (1996): "There is no generally accepted word for a set with a not necessarily associative binary operation. The word groupoid is used by many universal algebraists, but workers in category theory and related areas object strongly to this usage because they use the same word to mean 'category in which all morphisms are invertible'. The term magma was used by Serre [Lie Algebras and Lie Groups, 1965]."^[4] It also appears in Bourbaki's Éléments de mathématique, Algèbre, chapitres 1 à 3, 1970.^[5]

Definition

A magma is a set M matched with an operation • that sends any two elements a, b ∈ M to another element, a • b ∈ M. The symbol • is a general placeholder for a properly defined operation. To qualify as a magma, the set and operation (M, •) must satisfy the following requirement (known as the magma or closure axiom):

For all a, b in M, the result of the operation a • b is also in M.

And in mathematical notation:

a,b\in M\implies a\cdot b\in M.

If • is instead a partial operation, then (M, •) is called a partial magma^[6] or, more often, a partial groupoid.^[6]^[7]

Morphism of magmas

A morphism of magmas is a function f : M → N that maps magma (M, •) to magma (N, ∗) that preserves the binary operation:

f (x • y) = f(x) ∗ f(y).

Notation and combinatorics

The magma operation may be applied repeatedly, and in the general, non-associative case, the order matters, which is notated with parentheses. Also, the operation • is often omitted and notated by juxtaposition:

(a • (b • c)) • d \equiv (a (bc)) d

.

A shorthand is often used to reduce the number of parentheses, in which the innermost operations and pairs of parentheses are omitted, being replaced just with juxtaposition: $xy • z \equiv (x • y) • z$ . For example, the above is abbreviated to the following expression, still containing parentheses:

(a • bc) d

.

A way to avoid completely the use of parentheses is prefix notation, in which the same expression would be written $•• a • bcd$ . Another way, familiar to programmers, is postfix notation (reverse Polish notation), in which the same expression would be written $abc •• d •$ , in which the order of execution is simply left-to-right (no currying).

The set of all possible strings consisting of symbols denoting elements of the magma, and sets of balanced parentheses is called the Dyck language. The total number of different ways of writing $n$ applications of the magma operator is given by the Catalan number $C n$ . Thus, for example, $C 2 = 2$ , which is just the statement that $(ab) c$ and $a (bc)$ are the only two ways of pairing three elements of a magma with two operations. Less trivially, $C 3 = 5$ : $((ab) c) d$ , $(a (bc)) d$ , $(ab)(cd)$ , $a ((bc) d)$ , and $a (b (cd))$ .

There are $n n 2$ magmas with $n$ elements, so there are 1, 1, 16, 19683, 4294967296, ... (sequence A002489 in the OEIS) magmas with 0, 1, 2, 3, 4, ... elements. The corresponding numbers of non-isomorphic magmas are 1, 1, 10, 3330, 178981952, ... (sequence A001329 in the OEIS) and the numbers of simultaneously non-isomorphic and non-antiisomorphic magmas are 1, 1, 7, 1734, 89521056, ... (sequence A001424 in the OEIS).^[8]

Free magma

A free magma M_X on a set X is the "most general possible" magma generated by X (i.e., there are no relations or axioms imposed on the generators; see free object). The binary operation on M_X is formed by wrapping each of the two operands in parentheses and juxtaposing them in the same order. For example:

a • b = (a)(b),

a • (a • b) = (a)((a)(b)),

(a • a) • b = ((a)(a))(b).

M_X can be described as the set of non-associative words on X with parentheses retained.^[9]

It can also be viewed, in terms familiar in computer science, as the magma of full binary trees with leaves labelled by elements of X. The operation is that of joining trees at the root. It therefore has a foundational role in syntax.

A free magma has the universal property such that if f : X → N is a function from X to any magma N, then there is a unique extension of f to a morphism of magmas f′

f′ : M_X → N.

Types of magma

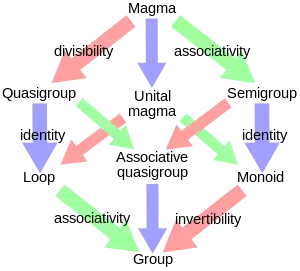
Algebraic structures from magmas to groups

Magmas are not often studied as such; instead there are several different kinds of magma, depending on what axioms the operation is required to satisfy. Commonly studied types of magma include:

Quasigroup: A magma where division is always possible.
- Loop: A quasigroup with an identity element.
Semigroup: A magma where the operation is associative.
- Monoid: A semigroup with an identity element.
Group: A magma with inverse, associativity, and an identity element.

Note that each of divisibility and invertibility imply the cancellation property.

Magmas with commutativity

Commutative magma: A magma with commutativity.
Commutative monoid: A monoid with commutativity.
Abelian group: A group with commutativity.

Classification by properties

Group-like structures
	Totality^α	Associativity	Identity	Divisibility^β	Commutativity
Partial magma	Unneeded	Unneeded	Unneeded	Unneeded	Unneeded
Semigroupoid	Unneeded	Required	Unneeded	Unneeded	Unneeded
Small category	Unneeded	Required	Required	Unneeded	Unneeded
Groupoid	Unneeded	Required	Required	Required	Unneeded
Magma	Required	Unneeded	Unneeded	Unneeded	Unneeded
Quasigroup	Required	Unneeded	Unneeded	Required	Unneeded
Unital magma	Required	Unneeded	Required	Unneeded	Unneeded
Loop	Required	Unneeded	Required	Required	Unneeded
Semigroup	Required	Required	Unneeded	Unneeded	Unneeded
Associative quasigroup	Required	Required	Unneeded	Required	Unneeded
Monoid	Required	Required	Required	Unneeded	Unneeded
Commutative monoid	Required	Required	Required	Unneeded	Required
Group	Required	Required	Required	Required	Unneeded
Abelian group	Required	Required	Required	Required	Required
^α The closure axiom, used by many sources and defined differently, is equivalent. ^β Here, divisibility refers specifically to the quasigroup axioms.

A magma $(S, •)$ , with $x, y, u, z$ ∈ $S$ , is called

Medial: If it satisfies the identity $xy • uz \equiv xu • yz$
Left semimedial: If it satisfies the identity $xx • yz \equiv xy • xz$
Right semimedial: If it satisfies the identity $yz • xx \equiv yx • zx$
Semimedial: If it is both left and right semimedial
Left distributive: If it satisfies the identity $x • yz \equiv xy • xz$
Right distributive: If it satisfies the identity $yz • x \equiv yx • zx$
Autodistributive: If it is both left and right distributive
Commutative: If it satisfies the identity $xy \equiv yx$
Idempotent: If it satisfies the identity $xx \equiv x$
Unipotent: If it satisfies the identity $xx \equiv yy$
Zeropotent: If it satisfies the identities $xx • y \equiv xx \equiv y • xx$ ^[10]
Alternative: If it satisfies the identities $xx • y \equiv x • xy$ and $x • yy \equiv xy • y$
Power-associative: If the submagma generated by any element is associative
Flexible: if $xy • x \equiv x • yx$
Associative: If it satisfies the identity $x • yz \equiv xy • z$ , called a semigroup
A left unar: If it satisfies the identity $xy \equiv xz$
A right unar: If it satisfies the identity $yx \equiv zx$
Semigroup with zero multiplication, or null semigroup: If it satisfies the identity $xy \equiv uv$
Unital: If it has an identity element
Left-cancellative: If, for all $x, y, z$ , relation $xy = xz$ implies $y = z$
Right-cancellative: If, for all $x, y, z$ , relation $yx = zx$ implies $y = z$
Cancellative: If it is both right-cancellative and left-cancellative
A semigroup with left zeros: If it is a semigroup and it satisfies the identity $xy \equiv x$
A semigroup with right zeros: If it is a semigroup and it satisfies the identity $yx \equiv x$
Trimedial: If any triple of (not necessarily distinct) elements generates a medial submagma
Entropic: If it is a homomorphic image of a medial cancellation magma.^[11]

Category of magmas

The category of magmas, denoted Mag, is the category whose objects are magmas and whose morphisms are magma homomorphisms. The category Mag has direct products, and there is an inclusion functor: Set → Med ↪ Mag as trivial magmas, with operations given by projection $x T y = y$ .

An important property is that an injective endomorphism can be extended to an automorphism of a magma extension, just the colimit of the (constant sequence of the) endomorphism.

Because the singleton $({*}, *)$ is the terminal object of Mag, and because Mag is algebraic, Mag is pointed and complete.^[12]

References

↑ Bergman, Clifford (2011), Universal Algebra: Fundamentals and Selected Topics, CRC Press, ISBN 978-1-4398-5130-2
↑ Hausmann, B. A.; Ore, Øystein (October 1937), "Theory of quasi-groups", American Journal of Mathematics, 59 (4): 983–1004, doi:10.2307/2371362, JSTOR 2371362.
↑ Hollings, Christopher (2014), Mathematics across the Iron Curtain: A History of the Algebraic Theory of Semigroups, American Mathematical Society, pp. 142–143, ISBN 978-1-4704-1493-1.
↑ Bergman, George M.; Hausknecht, Adam O. (1996), Cogroups and Co-rings in Categories of Associative Rings, American Mathematical Society, p. 61, ISBN 978-0-8218-0495-7.
↑ Bourbaki, N. (1998) [1970], "Algebraic Structures: §1.1 Laws of Composition: Definition 1", Algebra I: Chapters 1–3, Springer, p. 1, ISBN 978-3-540-64243-5.
1 2 Müller-Hoissen, Folkert; Pallo, Jean Marcel; Stasheff, Jim, eds. (2012), Associahedra, Tamari Lattices and Related Structures: Tamari Memorial Festschrift, Springer, p. 11, ISBN 978-3-0348-0405-9.
↑ Evseev, A. E. (1988), "A survey of partial groupoids", in Silver, Ben (ed.), Nineteen Papers on Algebraic Semigroups, American Mathematical Society, ISBN 0-8218-3115-1.
↑ Weisstein, Eric W. "Groupoid". MathWorld.
↑ Rowen, Louis Halle (2008), "Definition 21B.1.", Graduate Algebra: Noncommutative View, Graduate Studies in Mathematics, American Mathematical Society, p. 321, ISBN 0-8218-8408-5.
↑ Kepka, T.; Němec, P. (1996), "Simple balanced groupoids" (PDF), Acta Universitatis Palackianae Olomucensis. Facultas Rerum Naturalium. Mathematica, 35 (1): 53–60.
↑ Ježek, Jaroslav; Kepka, Tomáš (1981), "Free entropic groupoids" (PDF), Commentationes Mathematicae Universitatis Carolinae, 22 (2): 223–233, MR 0620359.
↑ Borceux, Francis; Bourn, Dominique (2004). Mal'cev, protomodular, homological and semi-abelian categories. Springer. pp. 7, 19. ISBN 1-4020-1961-0.

Hazewinkel, M. (2001) [1994], "Magma", Encyclopedia of Mathematics, EMS Press
Hazewinkel, M. (2001) [1994], "Groupoid", Encyclopedia of Mathematics, EMS Press
Hazewinkel, M. (2001) [1994], "Free magma", Encyclopedia of Mathematics, EMS Press
Weisstein, Eric W. "Groupoid". MathWorld.