In artificial intelligence, genetic programming (GP) is a technique of evolving programs, starting from a population of unfit (usually random) programs, fit for a particular task by applying operations analogous to natural genetic processes to the population of programs.

The operations are: selection of the fittest programs for reproduction (crossover), replication and/or mutation according to a predefined fitness measure, usually proficiency at the desired task. The crossover operation involves swapping specified parts of selected pairs (parents) to produce new and different offspring that become part of the new generation of programs. Some programs not selected for reproduction are copied from the current generation to the new generation. Mutation involves substitution of some random part of a program with some other random part of a program. Then the selection and other operations are recursively applied to the new generation of programs.

Typically, members of each new generation are on average more fit than the members of the previous generation, and the best-of-generation program is often better than the best-of-generation programs from previous generations. Termination of the evolution usually occurs when some individual program reaches a predefined proficiency or fitness level.

It may and often does happen that a particular run of the algorithm results in premature convergence to some local maximum which is not a globally optimal or even good solution. Multiple runs (dozens to hundreds) are usually necessary to produce a very good result. It may also be necessary to have a large starting population size and variability of the individuals to avoid pathologies.

History

The first record of the proposal to evolve programs is probably that of Alan Turing in 1950.[1] There was a gap of 25 years before the publication of John Holland's 'Adaptation in Natural and Artificial Systems' laid out the theoretical and empirical foundations of the science. In 1981, Richard Forsyth demonstrated the successful evolution of small programs, represented as trees, to perform classification of crime scene evidence for the UK Home Office.[2]

Although the idea of evolving programs, initially in the computer language Lisp, was current amongst John Holland’s students,[3] it was not until they organised the first Genetic Algorithms (GA) conference in Pittsburgh that Nichael Cramer[4] published evolved programs in two specially designed languages, which included the first statement of modern "tree-based" Genetic Programming (that is, procedural languages organized in tree-based structures and operated on by suitably defined GA-operators). In 1988, John Koza (also a PhD student of John Holland) patented his invention of a GA for program evolution.[5] This was followed by publication in the International Joint Conference on Artificial Intelligence IJCAI-89.[6]

Koza followed this with 205 publications on “Genetic Programming” (GP), name coined by David Goldberg, also a PhD student of John Holland.[7] However, it is the series of 4 books by Koza, starting in 1992[8] with accompanying videos,[9] that really established GP. Subsequently, there was an enormous expansion of the number of publications with the Genetic Programming Bibliography, surpassing 10,000 entries.[10] In 2010, Koza[11] listed 77 results where Genetic Programming was human competitive.

In 1996, Koza started the annual Genetic Programming conference[12] which was followed in 1998 by the annual EuroGP conference,[13] and the first book[14] in a GP series edited by Koza. 1998 also saw the first GP textbook.[15] GP continued to flourish, leading to the first specialist GP journal[16] and three years later (2003) the annual Genetic Programming Theory and Practice (GPTP) workshop was established by Rick Riolo.[17][18] Genetic Programming papers continue to be published at a diversity of conferences and associated journals. Today there are nineteen GP books including several for students.[15]

Foundational work in GP

Early work that set the stage for current genetic programming research topics and applications is diverse, and includes software synthesis and repair, predictive modeling, data mining,[19] financial modeling,[20] soft sensors,[21] design,[22] and image processing.[23] Applications in some areas, such as design, often make use of intermediate representations,[24] such as Fred Gruau’s cellular encoding.[25] Industrial uptake has been significant in several areas including finance, the chemical industry, bioinformatics[26][27] and the steel industry.[28]

Methods

Program representation

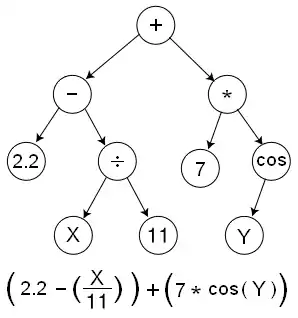
A function represented as a tree structure

GP evolves computer programs, traditionally represented in memory as tree structures.[29] Trees can be easily evaluated in a recursive manner. Every internal node has an operator function and every terminal node has an operand, making mathematical expressions easy to evolve and evaluate. Thus traditionally GP favors the use of programming languages that naturally embody tree structures (for example, Lisp; other functional programming languages are also suitable).

Non-tree representations have been suggested and successfully implemented, such as linear genetic programming which perhaps suits the more traditional imperative languages.[30][31] The commercial GP software Discipulus uses automatic induction of binary machine code ("AIM")[32] to achieve better performance. µGP[33] uses directed multigraphs to generate programs that fully exploit the syntax of a given assembly language. Multi expression programming uses Three-address code for encoding solutions. Other program representations on which significant research and development have been conducted include programs for stack-based virtual machines,[34][35][36] and sequences of integers that are mapped to arbitrary programming languages via grammars.[37][38] Cartesian genetic programming is another form of GP, which uses a graph representation instead of the usual tree based representation to encode computer programs.

Most representations have structurally noneffective code (introns). Such non-coding genes may seem to be useless because they have no effect on the performance of any one individual. However, they alter the probabilities of generating different offspring under the variation operators, and thus alter the individual's variational properties. Experiments seem to show faster convergence when using program representations that allow such non-coding genes, compared to program representations that do not have any non-coding genes.[39][40] Instantiations may have both trees with introns and those without; the latter are called canonical trees. Special canonical crossover operators are introduced that maintain the canonical structure of parents in their children.

Selection

Selection is a process whereby certain individuals are selected from the current generation that would serve as parents for the next generation. The individuals are selected probabilistically such that the better performing individuals have a higher chance of getting selected.[18] The most commonly used selection method in GP is tournament selection, although other methods such as fitness proportionate selection, lexicase selection,[41] and others have been demonstrated to perform better for many GP problems.

Elitism, which involves seeding the next generation with the best individual (or best n individuals) from the current generation, is a technique sometimes employed to avoid regression.

Crossover

In Genetic Programming two fit individuals are chosen from the population to be parents for one or two children. In tree genetic programming, these parents are represented as inverted lisp like trees, with their root nodes at the top. In subtree crossover in each parent a subtree is randomly chosen. (Highlighted with yellow in the animation.) In the root donating parent (in the animation on the left) the chosen subtree is removed and replaced with a copy of the randomly chosen subtree from the other parent, to give a new child tree.

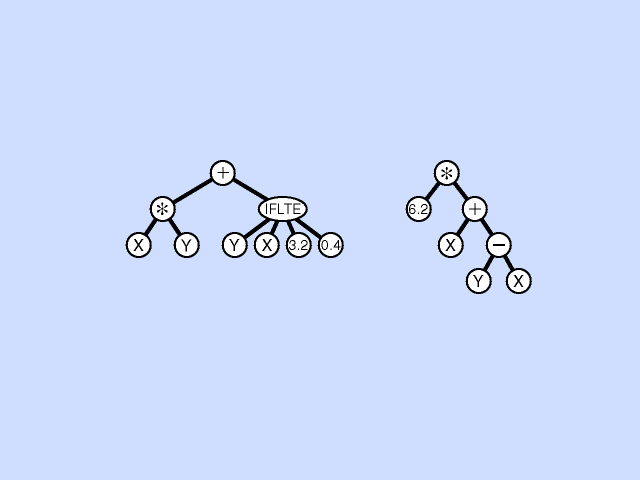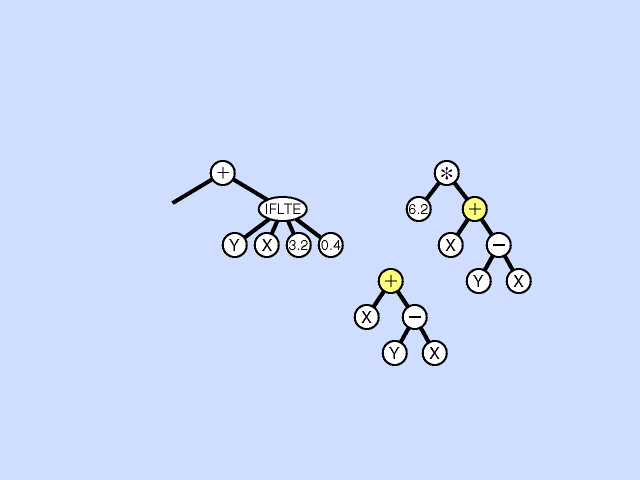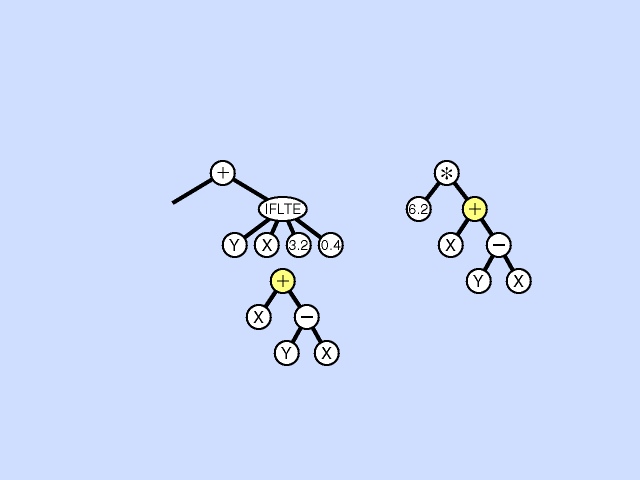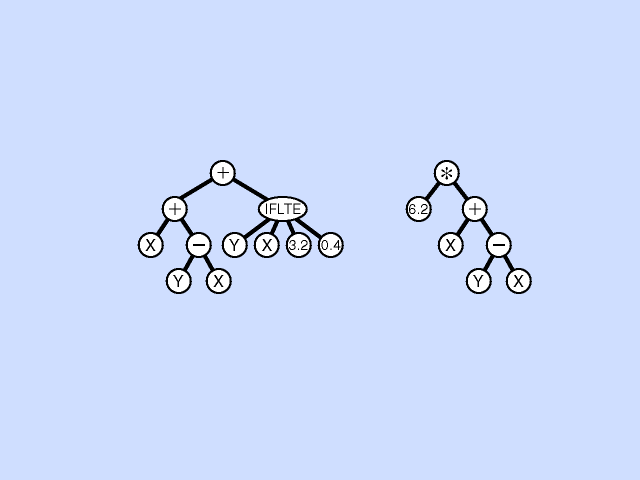
Sometimes two child crossover is used, in which case the removed subtree (in the animation on the left) is not simply deleted but is copied to a copy of the second parent (here on the right) replacing (in the copy) its randomly chosen subtree. Thus this type of subtree crossover takes two fit trees and generates two child trees. Genetic programming subtree crossover

Replication

Some individuals selected according to fitness criteria do not participate in crossover, but are copied into the next generation, akin to asexual reproduction in the natural world. They may be further subject to mutation.

Mutation

There are many types of mutation in genetic programming. They start from a fit syntactically correct parent and aim to randomly create a syntactically correct child. In the animation a subtree is randomly chosen (highlighted by yellow). It is removed and replaced by a randomly generated subtree.

Other mutation operators select a leaf (external node) of the tree and replace it with a randomly chosen leaf. Another mutation is to select at random a function (internal node) and replace it with another function with the same arity (number of inputs). Hoist mutation randomly chooses a subtree and replaces it with a subtree within itself. Thus hoist mutation is guaranteed to make the child smaller. Leaf and same arity function replacement ensure the child is the same size as the parent. Whereas subtree mutation (in the animation) may, depending upon the function and terminal sets, have a bias to either increase or decrease the tree size. Other subtree based mutations try to carefully control the size of the replacement subtree and thus the size of the child tree.

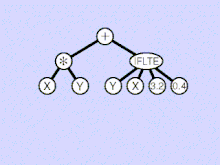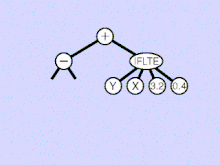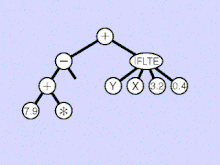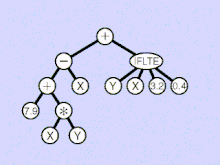
Animation of creating genetic programing child by mutating parent removing subtree and replacing with random code

Similarly there are many types of linear genetic programming mutation, each of which tries to ensure the mutated child is still syntactically correct.

Applications

GP has been successfully used as an automatic programming tool, a machine learning tool and an automatic problem-solving engine.[18] GP is especially useful in the domains where the exact form of the solution is not known in advance or an approximate solution is acceptable (possibly because finding the exact solution is very difficult). Some of the applications of GP are curve fitting, data modeling, symbolic regression, feature selection, classification, etc. John R. Koza mentions 76 instances where Genetic Programming has been able to produce results that are competitive with human-produced results (called Human-competitive results).[42] Since 2004, the annual Genetic and Evolutionary Computation Conference (GECCO) holds Human Competitive Awards (called Humies) competition,[43] where cash awards are presented to human-competitive results produced by any form of genetic and evolutionary computation. GP has won many awards in this competition over the years.

Meta-genetic programming

Meta-genetic programming is the proposed meta-learning technique of evolving a genetic programming system using genetic programming itself. It suggests that chromosomes, crossover, and mutation were themselves evolved, therefore like their real life counterparts should be allowed to change on their own rather than being determined by a human programmer. Meta-GP was formally proposed by Jürgen Schmidhuber in 1987.[44] Doug Lenat's Eurisko is an earlier effort that may be the same technique. It is a recursive but terminating algorithm, allowing it to avoid infinite recursion. In the "autoconstructive evolution" approach to meta-genetic programming, the methods for the production and variation of offspring are encoded within the evolving programs themselves, and programs are executed to produce new programs to be added to the population.[35][45]

Critics of this idea often say this approach is overly broad in scope. However, it might be possible to constrain the fitness criterion onto a general class of results, and so obtain an evolved GP that would more efficiently produce results for sub-classes. This might take the form of a meta evolved GP for producing human walking algorithms which is then used to evolve human running, jumping, etc. The fitness criterion applied to the meta GP would simply be one of efficiency.

See also

References

  1. ↑ "Computing Machinery and Intelligence". www.cs.bham.ac.uk. Retrieved 2018-05-19.
  2. ↑ "BEAGLE A Darwinian Approach to Pattern Recognition". www.cs.bham.ac.uk. Retrieved 2018-05-19.
  3. ↑ A personal communication with Tom Westerdale
  4. ↑ "A representation for the Adaptive Generation of Simple Sequential Programs". www.cs.bham.ac.uk. Retrieved 2018-05-19.
  5. ↑ "Non-Linear Genetic Algorithms for Solving Problems". www.cs.bham.ac.uk. Retrieved 2018-05-19.
  6. ↑ "Hierarchical genetic algorithms operating on populations of computer programs". www.cs.bham.ac.uk. Retrieved 2018-05-19.
  7. ↑ Goldberg. D.E. (1983), Computer-aided gas pipeline operation using genetic algorithms and rule learning. Dissertation presented to the University of Michigan at Ann Arbor, Michigan, in partial fulfillment of the requirements for Ph.D.
  8. ↑ "Genetic Programming: On the Programming of Computers by Means of Natural Selection". www.cs.bham.ac.uk. Retrieved 2018-05-19.
  9. ↑ "Genetic Programming:The Movie". gpbib.cs.ucl.ac.uk. Archived from the original on 2021-12-11. Retrieved 2021-05-20.
  10. ↑ "The effects of recombination on phenotypic exploration and robustness in evolution". gpbib.cs.ucl.ac.uk. Retrieved 2021-05-20.
  11. ↑ "Human-competitive results produced by genetic programming". www.cs.bham.ac.uk. Retrieved 2018-05-20.
  12. ↑ "Genetic Programming 1996: Proceedings of the First Annual Conference". www.cs.bham.ac.uk. Retrieved 2018-05-19.
  13. ↑ "Genetic Programming". www.cs.bham.ac.uk. Retrieved 2018-05-19.
  14. ↑ "Genetic Programming and Data Structures: Genetic Programming + Data Structures = Automatic Programming!". www.cs.bham.ac.uk. Retrieved 2018-05-20.
  15. 1 2 "Genetic Programming -- An Introduction; On the Automatic Evolution of Computer Programs and its Applications". www.cs.bham.ac.uk. Retrieved 2018-05-20.
  16. ↑ Banzhaf, Wolfgang (2000-04-01). "Editorial Introduction". Genetic Programming and Evolvable Machines. 1 (1–2): 5–6. doi:10.1023/A:1010026829303. ISSN 1389-2576.
  17. ↑ "Genetic Programming Theory and Practice". www.cs.bham.ac.uk. Retrieved 2018-05-20.
  18. 1 2 3 "A Field Guide to Genetic Programming". www.gp-field-guide.org.uk. Retrieved 2018-05-20.
  19. ↑ "Data Mining and Knowledge Discovery with Evolutionary Algorithms". www.cs.bham.ac.uk. Retrieved 2018-05-20.
  20. ↑ "EDDIE beats the bookies". www.cs.bham.ac.uk. Retrieved 2018-05-20.
  21. ↑ "Applying Computational Intelligence How to Create Value". www.cs.bham.ac.uk. Retrieved 2018-05-20.
  22. ↑ "Human-competitive machine invention by means of genetic programming". www.cs.bham.ac.uk. Retrieved 2018-05-20.
  23. ↑ "Discovery of Human-Competitive Image Texture Feature Extraction Programs Using Genetic Programming". www.cs.bham.ac.uk. Retrieved 2018-05-20.
  24. ↑ "Three Ways to Grow Designs: A Comparison of Embryogenies for an Evolutionary Design Problem". www.cs.bham.ac.uk. Retrieved 2018-05-20.
  25. ↑ "Cellular encoding as a graph grammar - IET Conference Publication". ieeexplore.ieee.org: 17/1–1710. April 1993. Retrieved 2018-05-20.
  26. ↑ "Genetic Algorithm Decoding for the Interpretation of Infra-red Spectra in Analytical Biotechnology". www.cs.bham.ac.uk. Retrieved 2018-05-20.
  27. ↑ "Genetic Programming for Mining DNA Chip data from Cancer Patients". www.cs.bham.ac.uk. Retrieved 2018-05-20.
  28. ↑ "Genetic Programming and Jominy Test Modeling". www.cs.bham.ac.uk. Retrieved 2018-05-20.
  29. ↑ Nichael L. Cramer "A Representation for the Adaptive Generation of Simple Sequential Programs" Archived 2005-12-04 at the Wayback Machine.
  30. ↑ Genetic Programming: An Introduction, Wolfgang Banzhaf, Peter Nordin, Robert E. Keller, Frank D. Francone, Morgan Kaufmann, 1999. ISBN 978-1558605107
  31. ↑ Garnett Wilson and Wolfgang Banzhaf. "A Comparison of Cartesian Genetic Programming and Linear Genetic Programming"
  32. ↑ (Peter Nordin, 1997, Banzhaf et al., 1998, Section 11.6.2-11.6.3)
  33. ↑ Giovanni Squillero. "µGP (MicroGP)".
  34. ↑ "Stack-Based Genetic Programming". gpbib.cs.ucl.ac.uk. Retrieved 2021-05-20.
  35. 1 2 Spector, Lee; Robinson, Alan (2002-03-01). "Genetic Programming and Autoconstructive Evolution with the Push Programming Language". Genetic Programming and Evolvable Machines. 3 (1): 7–40. doi:10.1023/A:1014538503543. ISSN 1389-2576. S2CID 5584377.
  36. ↑ Spector, Lee; Klein, Jon; Keijzer, Maarten (2005-06-25). "The Push3 execution stack and the evolution of control". Proceedings of the 7th annual conference on Genetic and evolutionary computation. ACM. pp. 1689–1696. CiteSeerX 10.1.1.153.384. doi:10.1145/1068009.1068292. ISBN 978-1595930101. S2CID 11954638.
  37. ↑ Ryan, Conor; Collins, JJ; Neill, Michael O (1998). Lecture Notes in Computer Science. Berlin, Heidelberg: Springer Berlin Heidelberg. pp. 83–96. CiteSeerX 10.1.1.38.7697. doi:10.1007/bfb0055930. ISBN 9783540643609.
  38. ↑ O'Neill, M.; Ryan, C. (2001). "Grammatical evolution". IEEE Transactions on Evolutionary Computation. 5 (4): 349–358. doi:10.1109/4235.942529. ISSN 1089-778X. S2CID 10391383.
  39. ↑ Julian F. Miller. "Cartesian Genetic Programming" Archived 2015-09-24 at the Wayback Machine. p. 19.
  40. ↑ Janet Clegg; James Alfred Walker; Julian Francis Miller. A New Crossover Technique for Cartesian Genetic Programming". 2007.
  41. ↑ Spector, Lee (2012). "Assessment of problem modality by differential performance of lexicase selection in genetic programming". Proceedings of the 14th annual conference companion on Genetic and evolutionary computation. Gecco '12. ACM. pp. 401–408. doi:10.1145/2330784.2330846. ISBN 9781450311786. S2CID 3258264.
  42. ↑ Koza, John R (2010). "Human-competitive results produced by genetic programming". Genetic Programming and Evolvable Machines. 11 (3–4): 251–284. doi:10.1007/s10710-010-9112-3.
  43. ↑ "Humies =Human-Competitive Awards".
  44. ↑ "1987 THESIS ON LEARNING HOW TO LEARN, METALEARNING, META GENETIC PROGRAMMING,CREDIT-CONSERVING MACHINE LEARNING ECONOMY".
  45. ↑ GECCO '16 Companion : proceedings of the 2016 Genetic and Evolutionary Computation Conference : July 20-24, 2016, Denver, Colorado, USA. Neumann, Frank (Computer scientist), Association for Computing Machinery. SIGEVO. New York, New York. 20 July 2016. ISBN 9781450343237. OCLC 987011786.{{cite book}}: CS1 maint: location missing publisher (link) CS1 maint: others (link)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.