The angle of incidence, in geometric optics, is the angle between a ray incident on a surface and the line perpendicular (at 90 degree angle) to the surface at the point of incidence, called the normal. The ray can be formed by any waves, such as optical, acoustic, microwave, and X-ray. In the figure below, the line representing a ray makes an angle θ with the normal (dotted line). The angle of incidence at which light is first totally internally reflected is known as the critical angle. The angle of reflection and angle of refraction are other angles related to beams.

In computer graphics and geography, the angle of incidence is also known as the illumination angle of a surface with a light source, such as the Earth's surface and the Sun.[1] It can also be equivalently described as the angle between the tangent plane of the surface and another plane at right angles to the light rays.[2] This means that the illumination angle of a certain point on Earth's surface is 0° if the Sun is precisely overhead and that it is 90° at sunset or sunrise.

Determining the angle of reflection with respect to a planar surface is trivial, but the computation for almost any other surface is significantly more difficult.

Refraction of light at the interface between two media.

Grazing angle or glancing angle

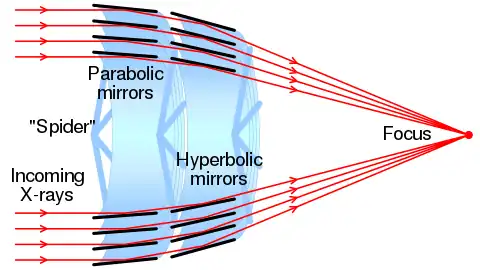
Focusing X-rays with glancing reflection

When dealing with a beam that is nearly parallel to a surface, it is sometimes more useful to refer to the angle between the beam and the surface tangent, rather than that between the beam and the surface normal. The 90-degree complement to the angle of incidence is called the grazing angle or glancing angle. Incidence at small grazing angles is called "grazing incidence."

Grazing incidence diffraction is used in X-ray spectroscopy and atom optics, where significant reflection can be achieved only at small values of the grazing angle. Ridged mirrors are designed to reflect atoms coming at a small grazing angle. This angle is usually measured in milliradians. In optics, there is Lloyd's mirror.

See also

References

  1. ↑ Godse, A. P. (2008). Computer Graphics. Technical Publications. p. 292. ISBN 9788189411008.
  2. ↑ Hengl, Tomislav; Reuter, Hannes I. (2022). Geomorphometryoncepts, Software, Applications. Developments in soil science. Vol. 33. Farha. p. 202. ISBN 9780123743459.


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.