In mathematics, a jacket matrix is a square symmetric matrix of order n if its entries are non-zero and real, complex, or from a finite field, and
where In is the identity matrix, and
where T denotes the transpose of the matrix.
In other words, the inverse of a jacket matrix is determined its element-wise or block-wise inverse. The definition above may also be expressed as:
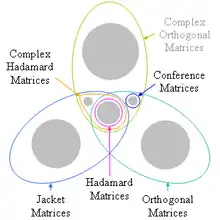
The jacket matrix is a generalization of the Hadamard matrix; it is a diagonal block-wise inverse matrix.
Motivation
| n | .... −2, −1, 0 1, 2,..... | logarithm |
| 2n | .... 1, 2, 4, ... | series |
As shown in the table, i.e. in the series, for example with n=2, forward: , inverse : , then, . That is, there exists an element-wise inverse.
Example 1.
- :
or more general
- :
Example 2.
For m x m matrices,
denotes an mn x mn block diagonal Jacket matrix.
Example 3.
- , and .
Therefore,
- .
Also,
- ,.
Finally,
A·B = B·A = I
Example 4.
Consider be 2x2 block matrices of order
- .
If and are pxp Jacket matrix, then is a block circulant matrix if and only if , where rt denotes the reciprocal transpose.
Example 5.
Let and , then the matrix is given by
- ,
- ⇒
where U, C, A, G denotes the amount of the DNA nucleobases and the matrix is the block circulant Jacket matrix which leads to the principle of the Antagonism with Nirenberg Genetic Code matrix.
References
[1] Moon Ho Lee, "The Center Weighted Hadamard Transform", IEEE Transactions on Circuits Syst. Vol. 36, No. 9, PP. 1247–1249, Sept. 1989.
[2] Kathy Horadam, Hadamard Matrices and Their Applications, Princeton University Press, UK, Chapter 4.5.1: The jacket matrix construction, PP. 85–91, 2007.
[3] Moon Ho Lee, Jacket Matrices: Constructions and Its Applications for Fast Cooperative Wireless Signal Processing, LAP LAMBERT Publishing, Germany, Nov. 2012.
[4] Moon Ho Lee, et. al., "MIMO Communication Method and System using the Block Circulant Jacket Matrix," US patent, no. US 009356671B1, May, 2016.
[5] S. K. Lee and M. H. Lee, “The COVID-19 DNA-RNA Genetic Code Analysis Using Information Theory of Double Stochastic Matrix,” IntechOpen, Book Chapter, April 17th, 2022. [Available in Online: https://www.intechopen.com/chapters/81329].