${\displaystyle {\frac {2}{\pi }}x\leq \sin(x)\leq x{\text{ for }}x\in \left[0,{\frac {\pi }{2}}\right]}$

unit circle with angle x and a second circle with radius ${\displaystyle |EG|=\sin(x)}$ around E. ${\displaystyle {\begin{aligned}&|DE|\leq |{\widehat {DC}}|\leq |{\widehat {DG}}|\\\Leftrightarrow &\sin(x)\leq x\leq {\tfrac {\pi }{2}}\sin(x)\\\Rightarrow &{\tfrac {2}{\pi }}x\leq \sin(x)\leq x\end{aligned}}}$

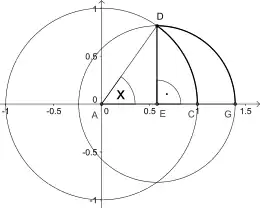
In mathematics, Jordan's inequality, named after Camille Jordan, states that^[1]

${\displaystyle {\frac {2}{\pi }}x\leq \sin(x)\leq x{\text{ for }}x\in \left[0,{\frac {\pi }{2}}\right].}$

It can be proven through the geometry of circles (see drawing).^[2]

Notes

Further reading

• Serge Colombo: Holomorphic Functions of One Variable. Taylor & Francis 1983, ISBN 0677059507, p. 167-168 (online copy)
• Da-Wei Niu, Jian Cao, Feng Qi: Generealizations of Jordan's Inequality and Concerned Relations. U.P.B. Sci. Bull., Series A, Volume 72, Issue 3, 2010, ISSN 1223-7027
• Feng Qi: Jordan's Inequality: Refinements, Generealizations, Applications and related Problems Archived 2016-03-03 at the Wayback Machine. RGMIA Res Rep Coll (2006), Volume: 9, Issue: 3, Pages: 243–259
• Meng-Kuang Kuo: Refinements of Jordan's inequality. Journal of Inequalities and Applications 2011, 2011:130, doi:10.1186/1029-242X-2011-130

External links

• Jordan's inequality at the Proof Wiki
• Jordan's and Kober's inequalities at cut-the-knot.org
• Weisstein, Eric W. "Jordan's inequality". MathWorld.