Meridian Room (or Cassini Room) at the Paris Observatory, 61 avenue de l'Observatoire (14th arrondissement). The Paris meridian is traced on the floor.

The Paris meridian is a meridian line running through the Paris Observatory in Paris, France – now longitude 2°20′14.02500″ East. It was a long-standing rival to the Greenwich meridian as the prime meridian of the world. The "Paris meridian arc" or "French meridian arc" (French: la Méridienne de France) is the name of the meridian arc measured along the Paris meridian.[1]

The French meridian arc was important for French cartography, since the triangulations of France began with the measurement of the French meridian arc. Moreover, the French meridian arc was important for geodesy as it was one of the meridian arcs which were measured to determine the figure of the Earth via the arc measurement method.[1] The determination of the figure of the Earth was a problem of the highest importance in astronomy, as the diameter of the Earth was the unit to which all celestial distances had to be referred.[2]

History

French cartography and the figure of the Earth

Paris meridian is located in France
Paris meridian
Paris meridian
Paris meridian
Paris meridian
Paris meridian
Paris meridian
Paris meridian
Paris meridian
Paris meridian
Paris Observatory
Paris Observatory
Line of the Paris meridian
Map of the French coast, corrected by the Academy of Sciences in 1682

In the year 1634, France ruled by Louis XIII and Cardinal Richelieu, decided that the Ferro Meridian through the westernmost of the Canary Islands should be used as the reference on maps, since El Hierro (Ferro) was the most western position of the Ptolemy's world map.[3] It was also thought to be exactly 20 degrees west of Paris.[3] The astronomers of the French Academy of Sciences, founded in 1666, managed to clarify the position of El Hierro relative to the meridian of Paris, which gradually supplanted the Ferro meridian.[3] In 1666, Louis XIV of France had authorized the building of the Paris Observatory. On Midsummer's Day 1667, members of the Academy of Sciences traced the future building's outline on a plot outside town near the Port Royal abbey, with Paris meridian exactly bisecting the site north–south.[4] French cartographers would use it as their prime meridian for more than 200 years.[3] Old maps from continental Europe often have a common grid with Paris degrees at the top and Ferro degrees offset by 20 at the bottom.[3]

A French astronomer, Abbé Jean Picard, measured the length of a degree of latitude along the Paris meridian (arc measurement) and computed from it the size of the Earth during 1668–1670.[1] The application of the telescope to angular instruments was an important step. He was the first who in 1669, with the telescope, using such precautions as the nature of the operation requires, measured a precise arc of meridian (Picard's arc measurement). He measured with wooden rods a baseline of 5,663 toises, and a second or base of verification of 3,902 toises; his triangulation network extended from Malvoisine, near Paris, to Sourdon, near Amiens. The angles of the triangles were measured with a quadrant furnished with a telescope having cross-wires. The difference of latitude of the terminal stations was determined by observations made with a sector on a star in Cassiopeia, giving 1° 22′ 55″ for the amplitude. The terrestrial degree measurement gave the length of 57,060 toises, whence he inferred 6,538,594 toises for the Earth's diameter.[2][5]

Four generations of the Cassini family headed the Paris Observatory.[6] They directed the surveys of France for over 100 years.[6] Hitherto geodetic observations had been confined to the determination of the magnitude of the Earth considered as a sphere, but a discovery made by Jean Richer turned the attention of mathematicians to its deviation from a spherical form. This astronomer, having been sent by the Academy of Sciences of Paris to the island of Cayenne (now in French Guiana) in South America, for the purpose of investigating the amount of astronomical refraction and other astronomical objects, observed that his clock, which had been regulated at Paris to beat seconds, lost about two minutes and a half daily at Cayenne, and that to bring it to measure mean solar time it was necessary to shorten the pendulum by more than a line (about 1⁄12th of an in.). This fact, which was scarcely credited till it had been confirmed by the subsequent observations of Varin and Deshayes on the coasts of Africa and America, was first explained in the third book of Newton’s Principia, who showed that it could only be referred to a diminution of gravity arising either from a protuberance of the equatorial parts of the Earth and consequent increase of the distance from the centre, or from the counteracting effect of the centrifugal force. About the same time (1673) appeared Christiaan Huygens’ De Horologio Oscillatorio, in which for the first time were found correct notions on the subject of centrifugal force. It does not, however, appear that they were applied to the theoretical investigation of the figure of the Earth before the publication of Newton's Principia. In 1690 Huygens published his De Causa Gravitatis, which contains an investigation of the figure of the Earth on the supposition that the attraction of every particle is towards the centre.

Between 1684 and 1718 Giovanni Domenico Cassini and Jacques Cassini, along with Philippe de La Hire, carried a triangulation, starting from Picard's base in Paris and extending it northwards to Dunkirk and southwards to Collioure. They measured a base of 7,246 toises near Perpignan, and a somewhat shorter base near Dunkirk; and from the northern portion of the arc, which had an amplitude of 2° 12′ 9″, obtained 56,960 toises for the length of a degree; while from the southern portion, of which the amplitude was 6° 18′ 57″, they obtained 57,097 toises. The immediate inference from this was that, with the degree diminishing with increasing latitude, the Earth must be a prolate spheroid. This conclusion was totally opposed to the theoretical investigations of Newton and Huygens, and accordingly the Academy of Sciences of Paris determined to apply a decisive test by the measurement of arcs at a great distance from each other – one in the neighbourhood of the equator, the other in a high latitude. Thus arose the celebrated French Geodesic Missions, to the Equator and to Lapland, the latter directed by Pierre Louis Maupertuis.[2]

Map of France in 1720

In 1740 an account was published in the Paris Mémoires, by Cassini de Thury, of a remeasurement by himself and Nicolas Louis de Lacaille of the meridian of Paris. With a view to determine more accurately the variation of the degree along the meridian, they divided the distance from Dunkirk to Collioure into four partial arcs of about two degrees each, by observing the latitude at five stations. The results previously obtained by Giovanni Domenico and Jacques Cassini were not confirmed, but, on the contrary, the length of the degree derived from these partial arcs showed on the whole an increase with increasing latitude.[2]

The West Europe-Africa Meridian-arc

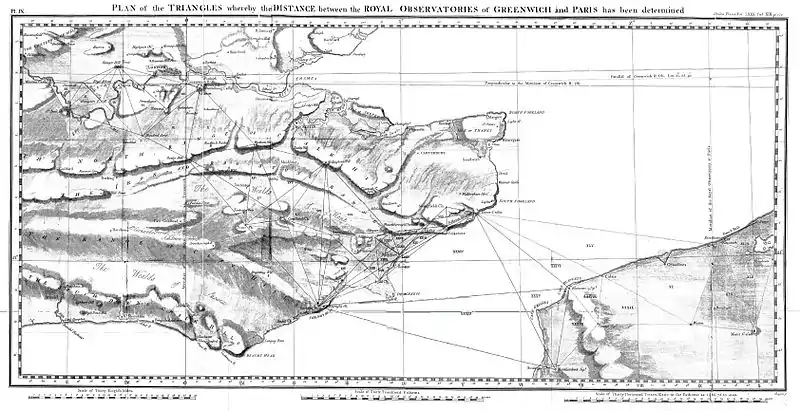
The triangulation mesh of the Anglo-French survey 1784–1790

Cesar-François Cassini de Thury completed the Cassini map, which was published by his son Cassini IV in 1790.[1] Moreover, the Paris meridian was linked with international collaboration in geodesy and metrology. Cesar-François Cassini de Thury (1714–1784) expressed the project to extend the French geodetic network all around the world and to connect the Paris and Greenwich observatories.[7] In 1783 the French Academy of Science presented his proposal to King George III.[7] This connection and a proposal from General William Roy led to the first triangulation of Great Britain.[7] France and Great Britain surveys' connection was repeated by French astronomers and geodesists in 1787 by Cassini IV, in 1823–1825 by François Arago and in 1861–1862 by François Perrier.[7][8]

Between 1792 and 1798 Pierre Méchain and Jean-Baptiste Delambre surveyed the Paris meridian arc between Dunkirk and Barcelona (see meridian arc of Delambre and Méchain). They extrapolated from this measurement the distance from the North Pole to the Equator which was 5,130,740 toises. As the metre had to be equal to one ten-millionth of this distance, it was defined as 0,513074 toises or 443,296 lignes of the Toise of Peru (see below) and of the double-toise N° 1 of the apparatus which had been devised by Lavoisier and Borda for this survey at specified temperatures.[9][10]

In the early 19th century, the Paris meridian's arc was recalculated with greater precision between Shetland and the Balearic Islands by the astronomer François Arago, whose name now appears on the plaques or medallions tracing the route of the meridian through Paris (see below). Biot and Arago published their work as a fourth volume following the three volumes of "Bases du système métrique décimal ou mesure de l'arc méridien compris entre les parallèles de Dunkerque et Barcelone" (Basis for the decimal metric system or measurement of the meridian arc comprised between Dunkirk and Barcelona) by Delambre and Méchain.[11]

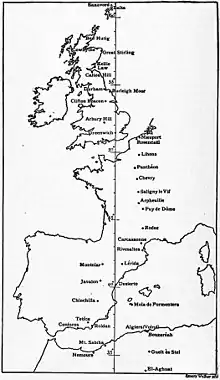
The West Europe-Africa Meridian-arc extending south from the Shetland Islands, through Great Britain, France and Spain to El Aghuat in Algeria, whose parameters were calculated from surveys carried out in the mid to late 19th century. It yielded a value for the equatorial radius of the Earth a = 6 377 935 metres, the ellipticity being assumed as 1/299.15. The radius of curvature of this arc is not uniform, being, in the mean, about 600 metres greater in the northern than in the southern part. The Greenwich meridian is depicted rather than the Paris meridian.[2]

In the second half of the 19th century, Carlos Ibáñez e Ibáñez de Ibero directed the survey of Spain.[12] From 1870 to 1894 the Paris meridan's arc was remeasured by Perrier and Bassot in France and Algeria.[6][8] In 1879, Ibáñez de Ibero for Spain and François Perrier for France directed the junction of the Spanish geodetic network with Algeria.[13] This connection was a remarkable enterprise where triangles with a maximum length of 270 km were observed from mountain stations over the Mediterranean Sea.[6][14] The triangulation of France was then connected to those of Great Britain, Spain and Algeria and thus the Paris meridian's arc measurement extended from Shetland to the Sahara.[13]

The fundamental co-ordinates of the Panthéon were also obtained anew, by connecting the Panthéon and the Paris Observatory with the five stations of Bry-sur-Marne, Morlu, Mont Valérien, Chatillon and Montsouris, where the observations of latitude and azimuth were effected.[2]

Geodesy and metrology

In 1860, the Russian Government at the instance of Otto Wilhelm von Struve invited the Governments of Belgium, France, Prussia and England to connect their triangulations to measure the length of an arc of parallel in latitude 52° and to test the accuracy of the figure and dimensions of the Earth, as derived from the measurements of arc of meridian.[15] To combine the measurements it was necessary to compare the geodetic standards of length used in the different countries.[15] The British Government invited those of France, Belgium, Prussia, Russia, India, Australia, Austria, Spain, United States and Cape of Good Hope to send their standards to the Ordnance Survey office in Southampton.[15] Notably the geodetic standards of France, Spain and United States were based on the metric system, whereas those of Prussia, Belgium and Russia where calibrated against the toise, of which the oldest physical representative was the Toise of Peru.[15][16][17] The Toise of Peru had been constructed in 1735 for Bouguer and De La Condamine as their standard of reference in the French Geodesic Mission, conducted in what is now Ecuador from 1735 to 1744 in collaboration with the Spanish officers Jorge Juan and Antonio de Ulloa.[15][18]

Alexander Ross Clarke and Henry James published the first results of the standards' comparisons in 1867.[15] The same year Russia, Spain and Portugal joined the Europäische Gradmessung and the General Conference of the association proposed the metre as a uniform length standard for the Arc measurement and recommended the establishment of an International Metre Commission.[18]

The Europäische Gradmessung decided the creation of an international geodetic standard at the General Conference held in Paris in 1875.[8] The Metre Convention was signed in 1875 in Paris and the International Bureau of Weights and Measures was created under the supervision of the International Committee for Weights and Measures.[18][19] The first president of the International Committee for Weights and Measures was the Spanish geodesist Carlos Ibáñez e Ibáñez de Ibero.[17] He also was the president of the Permanent Commission of the Europäische Gradmessung from 1874 to 1886.[18] In 1886 the association changed name for the International Geodetic Association (German: Internationale Erdmessung) and Carlos Ibáñez e Ibáñez de Ibero was reelected as president.[18][17] He remained in this position until his death in 1891.[17] During this period the International Geodetic Association gained worldwide importance with the joining of United States, Mexico, Chile, Argentina and Japan.[20] In 1883 the General Conference of the Europäische Gradmessung proposed to select the Greenwich meridian as the prime meridian in the hope that Great Britain would accede to the Metre Convention.[18][21]

From the Paris meridian to the Greenwich meridian

The United States passed an Act of Congress on 3 August 1882, authorizing President Chester A. Arthur to call an international conference to fix on a common prime meridian for time and longitude throughout the world. Before the invitations were sent out on 1 December, the joint efforts of Abbe, Fleming and William Frederick Allen, Secretary of the US railways' General Time Convention and Managing Editor of the Travellers' Official Guide to the Railways, had brought the US railway companies to an agreement which led to standard railway time being introduced at noon on 18 November 1883 across the nation. Although this was not legally established until 1918, there was thus a strong sense of fait accompli that preceded the International Meridian Conference, although setting local times was not part of the remit of the conference.

In 1884, at the International Meridian Conference in Washington DC, the Greenwich meridian was adopted as the prime meridian of the world. San Domingo, now the Dominican Republic, voted against. France and Brazil abstained. The United Kingdom acceded to the Metre Convention in 1884 and to the International Geodetic Association in 1898.[20][6] In 1911, Alexander Ross Clarke and Friedrich Robert Helmert stated in the Encyclopædia Britannica :

"According to the calculations made at the central bureau of the international association on the great meridian arc extending from the Shetland Islands, through Great Britain, France and Spain to El Aghuat in Algeria, a [the equatorial radius of the Earth] = 6,377,935 metres, the ellipticity being assumed as 1/299.15. [...] The net does not follow the meridian exactly, but deviates both to the west and to the east; actually, the meridian of Greenwich is nearer the mean than that of Paris (Helmert, Grösse d. Erde)."[2]

The French clung to the Paris meridian as a rival to Greenwich until 1911 for timekeeping purposes and 1914 for navigation.[21] To this day, French cartographers continue to indicate the Paris meridian on some maps.

From wireless telegraphy to Coordinated Universal Time

With the arrival of wireless telegraphy, France established a transmitter on the Eiffel Tower to broadcast a time signal.[21] The creation of the International Time Bureau, seated at the Paris Observatory, was decided upon during the 1912 Conférence internationale de l'heure radiotélégraphique. The following year an attempt was made to regulate the international status of the bureau through the creation of an international convention. However, the convention wasn't ratified by its member countries due to the outbreak of World War I. In 1919, after the war, it was decided upon to make the bureau the executive body of the International Commission of Time, one of the commissions of the then newly founded International Astronomical Union (IAU).

From 1956 until 1987 the International Time Bureau was part of the Federation of Astronomical and Geophysical Data Analysis Services (FAGS). In 1987 the bureau's tasks of combining different measurements of Atomic Time were taken over by the International Bureau of Weights and Measures (BIPM). Its tasks related to the correction of time with respect to the celestial reference frame and the Earth's rotation to realize the Coordinated Universal Time (UTC) were taken over by the International Earth Rotation and Reference Systems Service (IERS) which was established in its present form in 1987 by the International Astronomical Union and the International Union of Geodesy and Geophysics (IUGG).

The Arago medallions

One of the 135 Arago medallions. This one is located near the Louvre Pyramid.

In 1994 the Arago Association and the city of Paris commissioned a Dutch conceptual artist, Jan Dibbets, to create a memorial to Arago. Dibbets came up with the idea of setting 135 bronze medallions (although only 121 are documented in the official guide to the medallions) into the ground along the Paris meridian between the northern and southern limits of Paris: a total distance of 9.2 kilometres/5.7 miles. Each medallion is 12 cm in diameter and marked with the name ARAGO plus N and S pointers.

Another project, the Green Meridian (An 2000 – La Méridienne Verte), aimed to establish a plantation of trees along the entire length of the meridian arc in France. Several missing Arago medallions appear to have been replaced with the newer 'An 2000 – La Méridienne Verte' markers.

Unfounded speculation

In certain circles, some kind of occult or esoteric significance is ascribed to the Paris meridian; sometimes it is even perceived as a sinister axis. Dominique Stezepfandts, a French conspiracy theorist, attacks the Arago medallions that supposedly trace the route of "an occult geographical line". To him the Paris meridian is a "Masonic axis" or even "the heart of the Devil."

Henry Lincoln, in his book The Holy Place, argued that various ancient structures are aligned according to the Paris meridian. They even include medieval churches, built long before the meridian was established according to conventional history, and Lincoln found it obvious that the meridian "was based upon the 'cromlech intersect division line'." David Wood, in his book Genesis, likewise ascribes a deeper significance to the Paris meridian and takes it into account when trying to decipher the geometry of the myth-encrusted village of Rennes-le-Château: The meridian passes about 350 metres (1,150 ft) west of the site of the so-called "Poussin tomb," an important location in the legends and esoteric theories relating to that place. A sceptical discussion of these theories, including the supposed alignments, can be found in Bill Putnam and Edwin Wood's book The Treasure of Rennes-le-Château – A mystery solved.

In fiction

The confusion between the Greenwich and the Paris meridians is one of the plot elements of Tintin book Red Rackham's Treasure.[22]

The meridian line, dubbed the "Rose Line" by author Dan Brown, appeared in the novel The Da Vinci Code.

See also

48°50′11″N 2°20′14.025″E / 48.83639°N 2.33722917°E / 48.83639; 2.33722917

References

  1. 1 2 3 4 Paul., Murdin (2009). Full meridian of glory : perilous adventures in the competition to measure the Earth. New York: Copernicus Books/Springer. ISBN 9780387755335. OCLC 314175913.
  2. 1 2 3 4 5 6 7 Chisholm, Hugh, ed. (1911). "Earth, Figure of the" . Encyclopædia Britannica. Vol. 08 (11th ed.). Cambridge University Press.
  3. 1 2 3 4 5 LAGARDE, LUCIE (1979). "Historique du problème du Méridien origine en France". Revue d'Histoire des Sciences (in French). 32 (4): 289–304. doi:10.3406/rhs.1979.1638.
  4. ↑ Wolf, Charles (1827–1918) Auteur du texte (1902). Histoire de l'Observatoire de Paris, de sa fondation à 1793 / par C. Wolf,... Paris: Gauthier-Villars. pp. 1–12.{{cite book}}: CS1 maint: numeric names: authors list (link)
  5. ↑ Picard, Jean (1620–1682) Auteur du texte (1671). Mesure de la terre [par l'abbé Picard]. p. 23.{{cite book}}: CS1 maint: numeric names: authors list (link)
  6. 1 2 3 4 5 Torge, Wolfgang (2015). "From a Regional Project to an International Organization: The "Baeyer-Helmert-Era" of the International Association of Geodesy 1862–1916". IAG 150 Years. International Association of Geodesy Symposia. Vol. 143. Springer, Cham. pp. 3–18. doi:10.1007/1345_2015_42. ISBN 978-3-319-24603-1.
  7. 1 2 3 4 Martin, Jean-Pierre; McConnell, Anita (20 December 2008). "Joining the observatories of Paris and Greenwich". Notes and Records. 62 (4): 355–372. doi:10.1098/rsnr.2008.0029. ISSN 0035-9149.
  8. 1 2 3 Lebon, Ernest (1846–1922) Auteur du texte (1899). Histoire abrégée de l'astronomie / par Ernest Lebon,... Paris: Gauthier-Villars. pp. 165, 168–169, 171.{{cite book}}: CS1 maint: numeric names: authors list (link)
  9. ↑ Delambre, Jean-Baptiste (1749–1822) Auteur du texte; Méchain, Pierre (1744–1804) Auteur du texte (1806–1810). Base du système métrique décimal, ou Mesure de l'arc du méridien compris entre les parallèles de Dunkerque et Barcelone. T. 3 / , exécutée en 1792 et années suivantes, par MM. Méchain et Delambre, rédigée par M. Delambre,... pp. 139, 237.{{cite book}}: CS1 maint: numeric names: authors list (link)
  10. ↑ Débarbat, Suzanne; Quinn, Terry (1 January 2019). "Les origines du système métrique en France et la Convention du mètre de 1875, qui a ouvert la voie au Système international d'unités et à sa révision de 2018". Comptes Rendus Physique. 20 (1–2): 6–21. Bibcode:2019CRPhy..20....6D. doi:10.1016/j.crhy.2018.12.002. ISSN 1631-0705.
  11. ↑ Méchain, Pierre-François-André (1806). "ETH-Bibliothek Zürich / Base du système métrique décimal ou mesure de l'arc du méridien...". Baudouin. doi:10.3931/e-rara-11803. {{cite journal}}: Cite journal requires |journal= (help)
  12. ↑ J. Bertrand, Académie des sciences (France) Auteur du (1 January 1891). Comptes rendus hebdomadaires des séances de l'Académie des sciences / publiés... par MM. les secrétaires perpétuels. Notice sur le général Ibáñez, correspondant de l'Académie. Paris: Gauthier-Villars. pp. 266–269 p. 267.
  13. 1 2 Perrier, Académie des sciences (France) Auteur du (1 July 1879). Comptes rendus hebdomadaires des séances de l'Académie des sciences / publiés... par MM. les secrétaires perpétuels. Géodésie. – Jonction géodésique de l'Algérie avec l'Espagne, opération internationale exécutée sous la direction de MM. le général Ibañez et F. Perrier. Paris: Gauthier-Villars. pp. 885–889.
  14. ↑ BnF Catalogue général (in French). Imp. nationale. 1886. Retrieved 17 January 2018. {{cite book}}: |website= ignored (help)
  15. 1 2 3 4 5 6 Clarke, A. R.; James, Henry (1 January 1867). "Abstract of the Results of the Comparisons of the Standards of Length of England, France, Belgium, Prussia, Russia, India, Australia, Made at the Ordnance Survey Office, Southampton". Philosophical Transactions of the Royal Society of London. 157: 161–180. doi:10.1098/rstl.1867.0010. ISSN 0261-0523. S2CID 109333769.
  16. ↑ Clarke, A. R.; James, Henry (1 January 1873). "Results of the Comparisons of the Standards of Length of England, Austria, Spain, United States, Cape of Good Hope, and of a Second Russian Standard, Made at the Ordnance Survey Office, Southampton". Philosophical Transactions of the Royal Society of London. 163: 445–469. doi:10.1098/rstl.1873.0014. ISSN 0261-0523.
  17. 1 2 3 4 Soler, T. (1 February 1997). "A profile of General Carlos Ibáñez e Ibáñez de Ibero: first president of the International Geodetic Association". Journal of Geodesy. 71 (3): 176–188. Bibcode:1997JGeod..71..176S. doi:10.1007/s001900050086. ISSN 0949-7714. S2CID 119447198.
  18. 1 2 3 4 5 6 Torge, Wolfgang (2015). "From a Regional Project to an International Organization: The "Baeyer-Helmert-Era" of the International Association of Geodesy 1862–1916". IAG 150 Years. International Association of Geodesy Symposia. Vol. 143. Springer, Cham. pp. 3–18. doi:10.1007/1345_2015_42. ISBN 978-3-319-24603-1.
  19. ↑ "International Bureau of Weights and Measure Intergovernmental Organisation with headquarters located in Sèvres, France" (PDF). Bureau International des Poids et Mesures. Archived from the original (PDF) on 27 February 2005.
  20. 1 2 Torge, W. (1 April 2005). "The International Association of Geodesy 1862 to 1922: from a regional project to an international organization". Journal of Geodesy. 78 (9): 558–568. Bibcode:2005JGeod..78..558T. doi:10.1007/s00190-004-0423-0. ISSN 0949-7714. S2CID 120943411.
  21. 1 2 3 "The Greenwich Meridian – where east meets west: International Meridian Conference (1884)". thegreenwichmeridian.org. Retrieved 2 October 2017.
  22. ↑ "Collector's item: the submarine". Musée Hergé. Retrieved 13 February 2023. According to the coordinates provided by Sir François Haddock (which must be calculated in relation to the Paris Meridian and not the Greenwich Meridian, as Tintin reminds us), [...]
Wikimedia Commons has media related to Paris meridian.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.