In geometry, Monsky's theorem states that it is not possible to dissect a square into an odd number of triangles of equal area.[1] In other words, a square does not have an odd equidissection.

The problem was posed by Fred Richman in the American Mathematical Monthly in 1965 and was proved by Paul Monsky in 1970.[2][3][4]

Proof

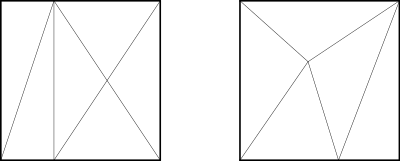
A square can be divided into an even number of triangles of equal area (left), but into an odd number of only approximately equal area triangles (right).

Monsky's proof combines combinatorial and algebraic techniques and in outline is as follows:

  1. Take the square to be the unit square with vertices at (0, 0), (0, 1), (1, 0) and (1, 1). If there is a dissection into n triangles of equal area, then the area of each triangle is 1/n.
  2. Colour each point in the square with one of three colours, depending on the 2-adic valuation of its coordinates.
  3. Show that a straight line can contain points of only two colours.
  4. Use Sperner's lemma to show that every triangulation of the square into triangles meeting edge-to-edge must contain at least one triangle whose vertices have three different colours.
  5. Conclude from the straight-line property that a tricolored triangle must also exist in every dissection of the square into triangles, not necessarily meeting edge-to-edge.
  6. Use Cartesian geometry to show that the 2-adic valuation of the area of a triangle whose vertices have three different colours is greater than 1. So every dissection of the square into triangles must contain at least one triangle whose area has a 2-adic valuation greater than 1.
  7. If n is odd, then the 2-adic valuation of 1/n is 1, so it is impossible to dissect the square into triangles all of which have area 1/n.[5]

Optimal dissections

By Monsky's theorem, it is necessary to have triangles with different areas to dissect a square into an odd number of triangles. Lower bounds for the area differences that must occur to dissect a square into an odd numbers of triangles and the optimal dissections have been studied.[6][7][8]

Generalizations

The theorem can be generalized to higher dimensions: an n-dimensional hypercube can only be divided into simplices of equal volume if the number of simplices is a multiple of n!.[2]

References

  1. ↑ Aigner, Martin; Ziegler, Günter M. (2010). "One square and an odd number of triangles". Proofs from The Book (4th ed.). Berlin: Springer-Verlag. pp. 131–138. doi:10.1007/978-3-642-00856-6_20. ISBN 978-3-642-00855-9.
  2. 1 2 Xu, Moor (April 4, 2012). Sperner's Lemma (PDF) (Technical report). University of California, Berkeley.
  3. ↑ Monsky, P. (1970). "On Dividing a Square into Triangles". The American Mathematical Monthly. 77 (2): 161–164. doi:10.2307/2317329. JSTOR 2317329. MR 0252233.
  4. ↑ Stein, S. (2004). Kleber, M.; Vakil, R. (eds.). "Cutting a Polygon into Triangles of Equal Areas". The Mathematical Intelligencer. 26: 17–21. doi:10.1007/BF02985395. S2CID 117930135.
  5. ↑ Verrill, H. A. (September 8, 2004). "Dissecting a square into triangles" (PDF). Louisiana State University. Archived from the original (PDF) on August 18, 2010. Retrieved 2010-08-18.
  6. ↑ Mansow, K. (2003), Ungerade Triangulierungen eines Quadrats von kleiner Diskrepanz (en. Odd triangulations of a square of small discrepancy) (Diplomarbeit), Germany: TU Berlin.
  7. ↑ Schulze, Bernd (1 July 2011). "On the area discrepancy of triangulations of squares and trapezoids". Electronic Journal of Combinatorics. 18 (1): #P137. doi:10.37236/624. Zbl 1222.52017.
  8. ↑ Labbé, Jean-Philippe; Rote, Günter; Ziegler, Günter M. (2018). "Area Difference Bounds for Dissections of a Square into an Odd Number of Triangles". Experimental Mathematics. 29 (3): 1–23. arXiv:1708.02891. doi:10.1080/10586458.2018.1459961. S2CID 3995120.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.