| ||||
|---|---|---|---|---|
| Cardinal | one half | |||
| Ordinal | 1⁄2th (halfth) | |||
| Binary | 0.12 | |||
| Ternary | 0.11111111113 | |||
| Senary | 0.36 | |||
| Octal | 0.48 | |||
| Duodecimal | 0.612 | |||
| Hexadecimal | 0.816 | |||
| Greek | ∠ | |||
| Egyptian hieroglyph | 𓐛 | |||
| Hebrew | חֵצִ | |||
| Malayalam | ൴ | |||
| Chinese | 半 | |||
| Tibetan | ༪ | |||
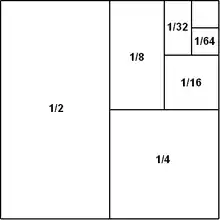
One half (pl.: halves) is the irreducible fraction resulting from dividing one (1) by two (2), or the fraction resulting from dividing any number by its double.
It often appears in mathematical equations, recipes, measurements, etc.
As a word
One half is one of the few fractions which are commonly expressed in natural languages by suppletion rather than regular derivation. In English, for example, compare the compound "one half" with other regular formations like "one-sixth".
A half can also be said to be one part of something divided into two equal parts. It is acceptable to write one half as a hyphenated word, one-half.
Mathematics
One half is the unique rational number that lies midway between nil and unity (which are the elementary additive and multiplicative identities) as the quotient of the first two non-zero integers, . It has two different decimal representations in base ten, the familiar and the recurring , with a similar pair of expansions in any even base; while in odd bases, one half has no terminating representation, it has only a single representation with a repeating fractional component (such as in ternary and in quinary).
Multiplication by one half is equivalent to division by two, or "halving"; conversely, division by one half is equivalent to multiplication by two, or "doubling".
A number raised to the power of one half is equal to the square root of ,
Properties
A hemiperfect number is a positive integer with a half-integer abundancy index:
where is odd, and is the sum-of-divisors function. The first three hemiperfect numbers are 2, 24, and 4320.[1]
The area of a triangle with base and altitude is computed as,

One half figures in the formula for calculating figurate numbers, such as the -th triangular number:
and in the formula for computing magic constants for magic squares,
Successive natural numbers yield the -th metallic mean by the equation,
In the study of finite groups, alternating groups have order
By Euler, a classical formula involving pi, and yielding a simple expression:[4]
where is the number of prime factors of the form of (see modular arithmetic).
For the gamma function, a non-integer argument of one half yields,
while inside Apéry's constant, which represents the sum of the reciprocals of all positive cubes, there is[5][6]
with the polygamma function of order on the complex numbers .
The upper half-plane is the set of points in the Cartesian plane with . In the context of complex numbers, the upper half-plane is defined as
In differential geometry, this is the universal covering space of surfaces with constant negative Gaussian curvature, by the uniformization theorem.
For equal to , Bernouilli numbers hold a value of . In the Riemann hypothesis, every nontrivial complex root of the Riemann zeta function has a real part equal to .
Computer characters
| ½ | |
|---|---|
vulgar fraction one half | |
| In Unicode | U+00BD |
| Different from | |
| Different from | ¼, ¾ |
One-half has its own code point in some early extensions of ASCII at 171 (AB16). In Unicode, it has its own code unit at U+00BD (decimal 189) in the C1 Controls and Latin-1 Supplement block and a cross-reference in the Number Forms block, rendering as ½.[7] The HTML entity is ½,[8] and its PC entry is Alt+0189.[9] The single-precision floating-point for ½ is 3F00000016.
In typewriters, one half is one of the few fractions to usually have a key of its own (see fractions).
See also

References
- ↑ Sloane, N. J. A. (ed.). "Sequence A159907 (Numbers n with half-integral abundancy index, sigma(n)/n equals k+1/2 with integer k.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2023-07-31.
- ↑ Ed Pegg Jr. (July 2000). "Commentary on weekly puzzles". Mathpuzzle. Retrieved 2023-08-17.
- ↑ Weisstein, Eric W. "Almost integer". MathWorld -- A WolframAlpha Resource. Retrieved 2023-08-17.
- ↑ Euler, Leonhard (1748). Introductio in analysin infinitorum (in Latin). Vol. 1. p. 244.
- ↑ Evgrafov, M. A.; Bezhanov, K. A.; Sidorov, Y. V.; Fedoriuk, M. V.; Shabunin, M. I. (1972). A Collection of Problems in the Theory of Analytic Functions (in Russian). Moscow: Nauka. p. 263 (Ex. 30.10.1).
- ↑ Bloch, Spencer; Masha, Vlasenko. "Gamma functions, monodromy and Apéry constants" (PDF). University of Chicago (Paper). pp. 1–34. S2CID 126076513.
- ↑ "Latin-1 Supplement". SYMBL. Retrieved 2023-07-18.
- ↑ "HTML Character Entity References". SYMBL. Retrieved 2023-07-18.
- ↑ "Alt Codes". Alt-Codes. Retrieved 2023-07-18.