Pollard's rho algorithm is an algorithm for integer factorization. It was invented by John Pollard in 1975.[1] It uses only a small amount of space, and its expected running time is proportional to the square root of the smallest prime factor of the composite number being factorized.
Core ideas
The algorithm is used to factorize a number , where is a non-trivial factor. A polynomial modulo , called (e.g., ), is used to generate a pseudorandom sequence. It is important to note that must be a polynomial. A starting value, say 2, is chosen, and the sequence continues as , , , etc. The sequence is related to another sequence . Since is not known beforehand, this sequence cannot be explicitly computed in the algorithm. Yet, in it lies the core idea of the algorithm.
Because the number of possible values for these sequences is finite, both the sequence, which is mod , and sequence will eventually repeat, even though these values are unknown. If the sequences were to behave like random numbers, the birthday paradox implies that the number of before a repetition occurs would be expected to be , where is the number of possible values. So the sequence will likely repeat much earlier than the sequence . When one has found a such that but , the number is a multiple of , so has been found.
Once a sequence has a repeated value, the sequence will cycle, because each value depends only on the one before it. This structure of eventual cycling gives rise to the name "rho algorithm", owing to similarity to the shape of the Greek letter ρ when the values , , etc. are represented as nodes in a directed graph.

This is detected by Floyd's cycle-finding algorithm: two nodes and (i.e., and ) are kept. In each step, one moves to the next node in the sequence and the other moves forward by two nodes. After that, it is checked whether . If it is not 1, then this implies that there is a repetition in the sequence (i.e. . This works because if the is the same as , the difference between and is necessarily a multiple of . Although this always happens eventually, the resulting greatest common divisor (GCD) is a divisor of other than 1. This may be itself, since the two sequences might repeat at the same time. In this (uncommon) case the algorithm fails, and can be repeated with a different parameter.
Algorithm
The algorithm takes as its inputs n, the integer to be factored; and , a polynomial in x computed modulo n. In the original algorithm, , but nowadays it is more common to use . The output is either a non-trivial factor of n, or failure. It performs the following steps:[2]
Pseudocode for Pollard's rho algorithm
x ← 2 // starting value
y ← x
d ← 1
while d = 1:
x ← g(x)
y ← g(g(y))
d ← gcd(|x - y|, n)
if d = n:
return failure
else:
return d
Here x and y corresponds to and in the previous section. Note that this algorithm may fail to find a nontrivial factor even when n is composite. In that case, the method can be tried again, using a starting value other than 2 or a different .
Example factorization
Let and .
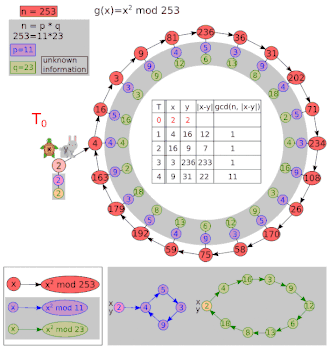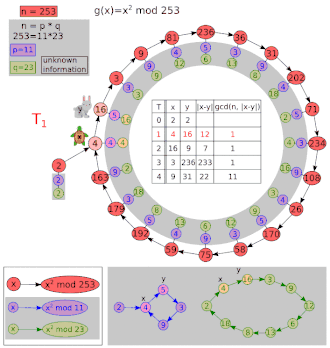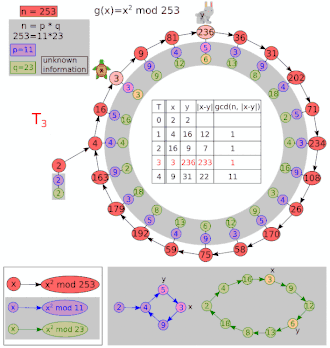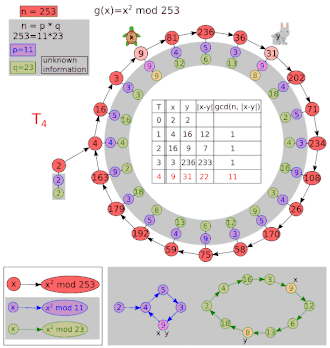
| i | x | y | gcd(|x − y|, 8051) |
|---|---|---|---|
| 1 | 5 | 26 | 1 |
| 2 | 26 | 7474 | 1 |
| 3 | 677 | 871 | 97 |
| 4 | 7474 | 1481 | 1 |
Now 97 is a non-trivial factor of 8051. Starting values other than x = y = 2 may give the cofactor (83) instead of 97. One extra iteration is shown above to make it clear that y moves twice as fast as x. Note that even after a repetition, the GCD can return to 1.
Variants
In 1980, Richard Brent published a faster variant of the rho algorithm. He used the same core ideas as Pollard but a different method of cycle detection, replacing Floyd's cycle-finding algorithm with the related Brent's cycle finding method.[3]
A further improvement was made by Pollard and Brent. They observed that if , then also for any positive integer . In particular, instead of computing at every step, it suffices to define as the product of 100 consecutive terms modulo , and then compute a single . A major speed up results as 100 gcd steps are replaced with 99 multiplications modulo and a single gcd. Occasionally it may cause the algorithm to fail by introducing a repeated factor, for instance when is a square. But it then suffices to go back to the previous gcd term, where , and use the regular ρ algorithm from there.
Application
The algorithm is very fast for numbers with small factors, but slower in cases where all factors are large. The ρ algorithm's most remarkable success was the 1980 factorization of the Fermat number F8 = 1238926361552897 × 93461639715357977769163558199606896584051237541638188580280321.[4] The ρ algorithm was a good choice for F8 because the prime factor p = 1238926361552897 is much smaller than the other factor. The factorization took 2 hours on a UNIVAC 1100/42.[4]
Example: factoring n = 10403 = 101 · 103
The following table shows numbers produced by the algorithm, starting with and using the polynomial . The third and fourth columns of the table contain additional information not known by the algorithm. They are included to show how the algorithm works.
| step | ||||
|---|---|---|---|---|
| 2 | 2 | 2 | 2 | 0 |
| 5 | 2 | 5 | 2 | 1 |
| 26 | 2 | 26 | 2 | 2 |
| 677 | 26 | 71 | 26 | 3 |
| 598 | 26 | 93 | 26 | 4 |
| 3903 | 26 | 65 | 26 | 5 |
| 3418 | 26 | 85 | 26 | 6 |
| 156 | 3418 | 55 | 85 | 7 |
| 3531 | 3418 | 97 | 85 | 8 |
| 5168 | 3418 | 17 | 85 | 9 |
| 3724 | 3418 | 88 | 85 | 10 |
| 978 | 3418 | 69 | 85 | 11 |
| 9812 | 3418 | 15 | 85 | 12 |
| 5983 | 3418 | 24 | 85 | 13 |
| 9970 | 3418 | 72 | 85 | 14 |
| 236 | 9970 | 34 | 72 | 15 |
| 3682 | 9970 | 46 | 72 | 16 |
| 2016 | 9970 | 97 | 72 | 17 |
| 7087 | 9970 | 17 | 72 | 18 |
| 10289 | 9970 | 88 | 72 | 19 |
| 2594 | 9970 | 69 | 72 | 20 |
| 8499 | 9970 | 15 | 72 | 21 |
| 4973 | 9970 | 24 | 72 | 22 |
| 2799 | 9970 | 72 | 72 | 23 |
The first repetition modulo 101 is 97 which occurs in step 17. The repetition is not detected until step 23, when . This causes to be , and a factor is found.
Complexity
If the pseudorandom number occurring in the Pollard ρ algorithm were an actual random number, it would follow that success would be achieved half the time, by the birthday paradox in iterations. It is believed that the same analysis applies as well to the actual rho algorithm, but this is a heuristic claim, and rigorous analysis of the algorithm remains open.[5]
See also
References
- ↑ Pollard, J. M. (1975). "A Monte Carlo method for factorization". BIT Numerical Mathematics. 15 (3): 331–334. doi:10.1007/bf01933667. S2CID 122775546.
- ↑ Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L. & Stein, Clifford (2009). "Section 31.9: Integer factorization". Introduction to Algorithms (third ed.). Cambridge, MA: MIT Press. pp. 975–980. ISBN 978-0-262-03384-8. (this section discusses only Pollard's rho algorithm).
- ↑ Brent, Richard P. (1980). "An Improved Monte Carlo Factorization Algorithm". BIT. 20 (2): 176–184. doi:10.1007/BF01933190. S2CID 17181286.
- 1 2 Brent, R.P.; Pollard, J. M. (1981). "Factorization of the Eighth Fermat Number". Mathematics of Computation. 36 (154): 627–630. doi:10.2307/2007666. JSTOR 2007666.
- ↑ Galbraith, Steven D. (2012). "14.2.5 Towards a rigorous analysis of Pollard rho". Mathematics of Public Key Cryptography. Cambridge University Press. pp. 272–273. ISBN 9781107013926..
Further reading
- Bai, Shi; Brent, Richard P. (January 2008). "On the Efficiency of Pollard's Rho Method for Discrete Logarithms". Conferences in Research and Practice in Information Technology, Vol. 77. The Australasian Theory Symposium (CATS2008). Wollongong. pp. 125–131. Describes the improvements available from different iteration functions and cycle-finding algorithms.
- Katz, Jonathan; Lindell, Yehuda (2007). "Chapter 8". Introduction to Modern Cryptography. CRC Press.
- Samuel S. Wagstaff, Jr. (2013). The Joy of Factoring. Providence, RI: American Mathematical Society. pp. 135–138. ISBN 978-1-4704-1048-3.