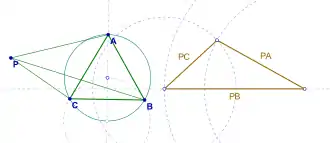
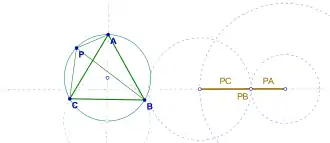
Pompeiu's theorem is a result of plane geometry, discovered by the Romanian mathematician Dimitrie Pompeiu. The theorem is simple, but not classical. It states the following:

Given an equilateral triangle ABC in the plane, and a point P in the plane of the triangle ABC, the lengths PA, PB, and PC form the sides of a (maybe, degenerate) triangle.^[1][2]

Proof of Pompeiu's theorem with Pompeiu triangle ${\displaystyle \triangle PCP'}$

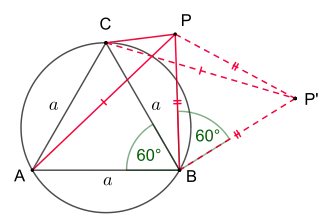
The proof is quick. Consider a rotation of 60° about the point B. Assume A maps to C, and P maps to P '. Then ${\displaystyle \scriptstyle PB\ =\ P'B}$, and ${\displaystyle \scriptstyle \angle PBP'\ =\ 60^{\circ }}$. Hence triangle PBP ' is equilateral and ${\displaystyle \scriptstyle PP'\ =\ PB}$. Then ${\displaystyle \scriptstyle PA\ =\ P'C}$. Thus, triangle PCP ' has sides equal to PA, PB, and PC and the proof by construction is complete (see drawing).^[1]

Further investigations reveal that if P is not in the interior of the triangle, but rather on the circumcircle, then PA, PB, PC form a degenerate triangle, with the largest being equal to the sum of the others, this observation is also known as Van Schooten's theorem.^[1]

Generally, by the point P and the lengths to the vertices of the equilateral triangle - PA, PB, and PC two equilateral triangles ( the larger and the smaller) with sides ${\displaystyle a_{1}}$ and ${\displaystyle a_{2}}$ are defined:

${\displaystyle {\begin{aligned}a_{1,2}^{2}&={\frac {1}{2}}\left(PA^{2}+PB^{2}+PC^{2}\pm 4{\sqrt {3}}\triangle _{(PA,PB,PC)}\right)\end{aligned}}}$.

The symbol △ denotes the area of the triangle whose sides have lengths PA, PB, PC.^[3]

Pompeiu published the theorem in 1936, however August Ferdinand Möbius had published a more general theorem about four points in the Euclidean plane already in 1852. In this paper Möbius also derived the statement of Pompeiu's theorem explicitly as a special case of his more general theorem. For this reason the theorem is also known as the Möbius-Pompeiu theorem.^[4]

External links

• MathWorld's page on Pompeiu's Theorem
• Pompeiu's theorem at cut-the-knot.org

Notes