Pong Hau K'i (Chinese: 裤裆棋; pinyin: kùdāng qí, Cantonese: Pong Hau K'i/bong1 hau2 kei4 崩口棋) is a Chinese traditional board game for two players. In Korea, it is known as Ou-moul-ko-no or Umul Gonu (우물고누)[1][2] or as Gang Gonu (강고누). "Umul" translates as "a spring", and the appearance of the board is like that of a spring in the center, with water running out in all directions. "Gang" translates as "river", and has a similar interpretation. Equivalent games are also played in Thailand (Sua tok tong) and in northern India (Hindustani?: Do-guti).
The board consists of 5 vertices and 7 edges. Each player has two pieces. Players take turns to move. At each turn, the player moves one of their two pieces into the adjacent vacant vertex. If a player can't move, they lose.
Only one type of position can make a player lose. If both players play perfectly, the game continues endlessly with no winner.
It is a children's game in both China and Korea, and is often used for childhood education.
One kind of board.
One kind of board, esp. for Pong Hau K'i.
One kind of board.
One kind of board, esp. for Umul Gonu.
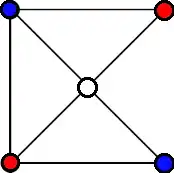
Starting position
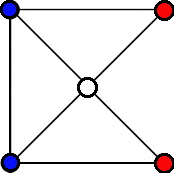
The starting position for Pong Hau K'i is shown on the left. The two players are "Red" and "Blue", with Red being the first player. The central spot is left unoccupied initially. The first move must be Red moving either of their pieces to the center. By symmetry, those two possible moves for Red are equivalent. The first three ply of moves for the two players are forced, and will always result in the position shown at the bottom.
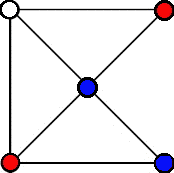
Umul Gonu begins differently: "Red" has both pieces at the top, and "Blue" has both pieces at the bottom. By itself, this would allow Red to win the game on their first move, so that particular first move is forbidden. The result is that the first three moves are also forced and, surprisingly, after three moves you find yourself in the same position as after three moves of Pong Hau K'i. The games, of course, are then equivalent.
Analysis
This game has been analyzed by P. Straffin,[3] who showed that it is a draw so long as both players can see 2-ply ahead, i.e. see the results of their move and of what their opponent would do in response. In particular, any win in Pong Hau K'i must go through the position shown on the left (or a symmetrically equivalent position). In this position, with Red to move, they have two choices: (1) They can move their top piece West along the top edge; or (2) They can move their bottom piece North along the left edge. In case (1), the game continues. But in case (2), the game will almost surely end quickly. If Blue then moves their bottom piece to the left, they win. If Blue is foolish enough to move their center piece instead, then Red wins by moving their top-right piece to the center. Thus with "2-ply lookahead", player Red can see the result of their (bad) move of the bottom piece (the first ply), realize that Blue then has a winning move (the second ply), and hence choose to not make that move.
Notes
References
- Bell, R. C. (1979). Board and table games from many civilizations.. (Revised Edition). New York: Dover Publications Inc. ISBN 0-486-23855-5
- Bell, R. C. (1980). Discovering old board games. (2nd Edition). Princes Risborough, Bucks.: Shire Publications. ISBN 0-85263-533-8
- Straffin, Philip D. (1995). "Position Graphs for Pong Hau K'i and Mu Torere". Mathematics Magazine, 68(5), Dec. 1995, pp. 382–386. "Corrected Figure for Position Graphs for Pong Hau K'i and Mu Torere". Mathematics Magazine, 69(1), Feb. 1996, p. 65.
See also
In China, there are some traditional board games like Pong Hau K'i.
In Korea, there are some traditional board games like Unul Gonu