< Portal:Mathematics < Selected picture
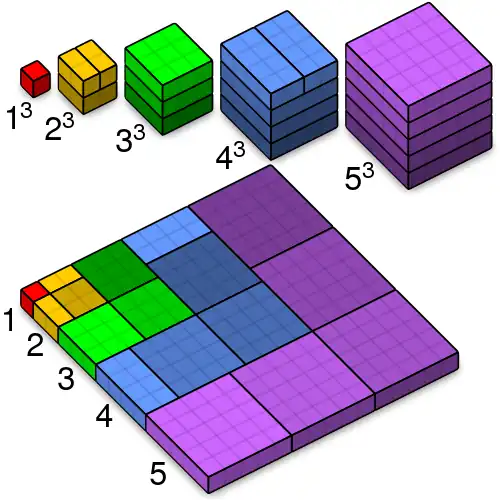

proof without words that the sum of the cubes of the first n natural numbers is the square of the sum of the first n natural numbers
Credit: Cmglee
Nicomachus's theorem states that the sum of the cubes of the first n natural numbers is the square of the sum of the first n natural numbers. This result is generalized by Faulhaber's formula, which gives the sum of pth powers of the first n natural numbers. The special case of Nicomachus's theorem can be proved by mathematical induction, but a more direct proof can be given which is illustrated by a proof without words, pictured here.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.