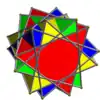
| Compound of 2n p/q-gonal antiprisms | |||
|---|---|---|---|
| |||
| Type | Uniform compound | ||
| Index |
| ||
| Polyhedra | 2n p/q-gonal antiprisms | ||
| Faces | 4n {p/q} (unless p/q=2), 4np triangles | ||
| Edges | 8np | ||
| Vertices | 4np | ||
| Symmetry group |
| ||
| Subgroup restricting to one constituent |
| ||
Each member of this infinite family of uniform polyhedron compounds is a symmetric arrangement of antiprisms sharing a common axis of rotational symmetry. It arises from superimposing two copies of the corresponding prismatic compound of antiprisms (without rotational freedom), and rotating each copy by an equal and opposite angle.
This infinite family can be enumerated as follows:
- For each positive integer n>0 and for each rational number p/q>3/2 (expressed with p and q coprime), there occurs the compound of 2n p/q-gonal antiprisms (with rotational freedom), with symmetry group:
- Dnpd if nq is odd
- Dnph if nq is even
Where p/q=2 the component is a tetrahedron, sometimes not considered a true antiprism.
References
- Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79 (3): 447–457, doi:10.1017/S0305004100052440, MR 0397554.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.