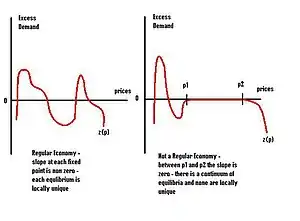
A regular economy is an economy characterized by an excess demand function which has the property that its slope at any equilibrium price vector is non-zero. In other words, if we graph the excess demand function against prices, then the excess demand function "cuts" the x-axis assuring that each equilibrium is locally unique. Local uniqueness in turn permits the use of comparative statics - an analysis of how the economy responds to external shocks - as long as these shocks are not too large.

An important result due to Debreu (1970) states that almost any economy, defined by an initial distribution of consumers' endowments, is regular. In technical terms, the set of nonregular economies is of Lebesgue measure zero.

Combined with the index theorem this result implies that almost any economy will have a finite (and odd) number of equilibria.

Regular and nonregular economies

References

• Debreu, G. (1970). Economies with a finite set of equilibria. Econometrica, 38 (3), 387–392.
• Dierker, E. (1972). Two Remarks on the Number of Equilibria of an Economy. Econometrica, 40 (5), 951–953.
• Mas-Colell, A., Whinston, M. and Green, J. (1995). Microeconomic Theory. Oxford University Press.