| Cuboctahedral pyramid | ||
|---|---|---|
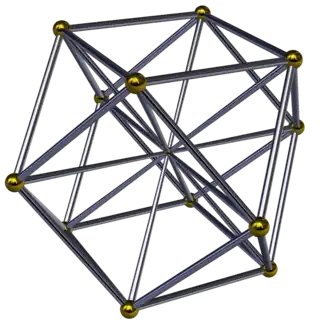 Schlegel diagram | ||
| Type | Polyhedral pyramid | |
| Schläfli symbol | ( ) ∨ r{4,3} | |
| Cells | 15 | 1 cuboctahedron 6 square pyramids 8 triangular pyramids |
| Faces | 38: | 8+24 triangles 6 squares |
| Edges | 36 | |
| Vertices | 13 | |
| Dual | rhombic dodecahedral pyramid | |
| Symmetry group | B3, [4,3,1], order 48 | |
| Properties | convex | |
In 4-dimensional geometry, the cuboctahedral pyramid is bounded by one cuboctahedron on the base, 6 square pyramid, and 8 triangular pyramid cells which meet at the apex. It has 38 faces: 32 triangles and 6 squares. It has 32 edges, and 13 vertices.
Since a cuboctahedron's circumradius is equal to its edge length,[1] the triangles must be taller than equilateral to create a positive height.
The dual to the cuboctahedral pyramid is a rhombic dodecahedral pyramid, seen as a rhombic dodecahedral base, and 12 rhombic pyramids meeting at an apex.
References
- ↑ Klitzing, Richard. "3D convex uniform polyhedra o3x4o - co".
External links
- Olshevsky, George. "Pyramid". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Richard Klitzing, Axial-Symmetrical Edge Facetings of Uniform Polyhedra
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
