The Soddy line of a triangle is the line that goes through the centers of the two Soddy circles of that triangle.

The Soddy line intersects the Euler line in the de Longchamps point and the Gergonne line in the Fletcher point. It is also perpendicular to the Gergonne line and together all three lines form the Euler-Gergonne-Soddy triangle. The Gergonne point and the incenter of the triangle are located on the Soddy line as well.

The line is named after Nobel laureate Frederick Soddy, who published a proof of a special case of Descartes' theorem about tangent circles as a poem in Nature in 1936.

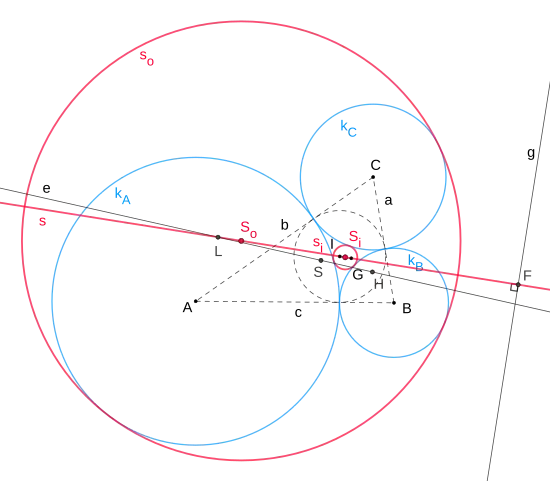
Soddy line ${\displaystyle s}$ (rot), outer Soddy center ${\displaystyle S_{o}}$, inner Soddy center ${\displaystyle S_{i}}$, Gergonne point ${\displaystyle G}$, incenter ${\displaystyle I}$, inner Soddy circle ${\displaystyle s_{i}}$, outer Soddy circle ${\displaystyle s_{o}}$, Fletcher point ${\displaystyle F}$, de Longchamps point ${\displaystyle L}$, Euler line ${\displaystyle e}$, Gergonne line ${\displaystyle g}$

References

• Zuming Feng: Why Are the Gergonne and Soddy Lines Perpendicular? A Synthetic Approach. In: Mathematics Magazin, Band 81, Nr. 3, Juni 2008, S. 211-214 (JSTOR)
• Roger Alperin: The Gergonne and Soddy lines. In: Elemente der Mathematik,. Band 70, Nr. 1, 2015, S. 1-6 (online)

External links

Wikimedia Commons has media related to Soddy line.

• Weisstein, Eric W. "Soddy line". MathWorld.