The stacking-fault energy (SFE) is a materials property on a very small scale. It is noted as γSFE in units of energy per area.

A stacking fault is an interruption of the normal stacking sequence of atomic planes in a close-packed crystal structure. These interruptions carry a certain stacking-fault energy. The width of stacking fault is a consequence of the balance between the repulsive force between two partial dislocations on one hand and the attractive force due to the surface tension of the stacking fault on the other hand. The equilibrium width is thus partially determined by the stacking-fault energy. When the SFE is high the dissociation of a full dislocation into two partials is energetically unfavorable, and the material can deform either by dislocation glide or cross-slip. Lower SFE materials display wider stacking faults and have more difficulties for cross-slip. The SFE modifies the ability of a dislocation in a crystal to glide onto an intersecting slip plane. When the SFE is low, the mobility of dislocations in a material decreases.[1]

Material Brass Stainless Steel Ag (Silver) Au Si (Silicon) Ni (Nickel) Cu (Copper) Mg (Magnesium) Al (Aluminum)
SFE (mJ m−2) <10[2] <10[2] 25[2] 75[2] >42 90 [2][3] 70[4] -78[5] 125 [6] 160-250 [7][2]

Stacking faults and stacking fault energy

A stacking fault is an irregularity in the planar stacking sequence of atoms in a crystal – in FCC metals the normal stacking sequence is ABCABC etc., but if a stacking fault is introduced it may introduce an irregularity such as ABCBCABC into the normal stacking sequence. These irregularities carry a certain energy which is called the stacking-fault energy.

Influences on stacking fault energy

A graph of how SFE quickly diminishes with zinc alloy content. Data taken from.[8][5]
A graph of how SFE quickly diminishes with aluminum alloy content. Data taken from.[8][4][9]

Stacking fault energy is heavily influenced by a few major factors, specifically base metal, alloying metals, percent of alloy metals, and valence-electron to atom ratio.[10]

Alloying elements effects on SFE

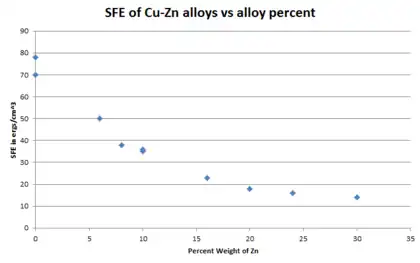
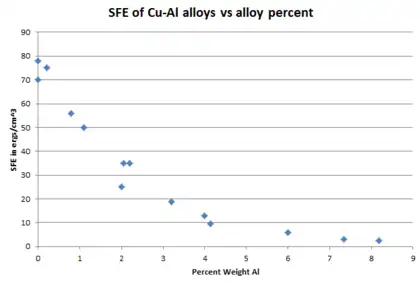
It has long been established that the addition of alloying elements significantly lowers the SFE of most metals.[4] Which element and how much is added dramatically affects the SFE of a material. The figures on the right show how the SFE of copper lowers with the addition of two different alloying elements; zinc and aluminum. In both cases, the SFE of the brass decreases with increasing alloy content. However, the SFE of the Cu-Al alloy decreases faster and reaches a lower minimum.

e/a ratio

Another factor that has a significant effect on the SFE of a material and is very interrelated with alloy content is the e/a ratio, or the ratio of valence electrons to atoms. Thornton[10] showed this in 1962 by plotting the e/a ratio vs SFE for a few Cu based alloys. He found that the valence-electron to atom ratio is a good predictor of stacking fault energy, even when the alloying element is changed. This directly supports the graphs on the right. Zinc is a heavier element and only has two valence electrons, whereas aluminum is lighter and has three valence electrons. Thus each weight percent of aluminum has a much greater impact on the SFE of the Cu-based alloy than does zinc.

Effects of stacking fault energy on deformation and texture

The two primary methods of deformation in metals are slip and twinning. Slip occurs by dislocation glide of either screw or edge dislocations within a slip plane. Slip is by far the most common mechanism. Twinning is less common but readily occurs under some circumstances.

Twinning occurs when there are not enough slip systems to accommodate deformation and/or when the material has a very low SFE. Twins are abundant in many low SFE metals like copper alloys, but are rarely seen in high SFE metals like aluminum.[11][8][4][9][5]

In order to accommodate large strains without fracturing, there must be at least five independent and active slip systems. When cross-slip frequently occurs and certain other criteria are met, sometimes only three independent slip systems are needed for accommodating large deformations.[12][13]

Because of the different deformation mechanisms in high and low SFE materials, they develop different textures.

High SFE materials

High SFE materials deform by glide of full dislocations. Because there are no stacking faults, the screw dislocations may cross-slip. Smallman found that cross-slip happens under low stress for high SFE materials like aluminum (1964). This gives a metal extra ductility because with cross-slip it needs only three other active slip systems to undergo large strains.[12][13] This is true even when the crystal is not ideally oriented.

High SFE materials therefore do not need to change orientation in order to accommodate large deformations because of cross-slip. Some reorientation and texture development will occur as the grains move during deformation. Extensive cross-slip due to large deformation also causes some grain rotation.[14] However, this re-orientation of grains in high SFE materials is much less prevalent than in low SFE materials.

Low SFE materials

Low SFE materials twin and create partial dislocations. Partials form instead of screw dislocations. Screws which do exist cannot cross-slip across stacking faults, even under high stresses.[14] Five or more slip systems must be active for large deformations to occur because of the absence of cross-slip. For both the <111> and <100> directions there are six and eight different slip systems, respectively. If loading is not applied near one of those directions, five slip systems might be active. In this case, other mechanisms must also be in place to accommodate large strains.

Low SFE materials also twin when strained. If deformation twinning is combined with regular shear deformation, the grains eventually align towards a more preferred orientation.[12][15] When many different grains align a highly anisotropic texture is created.

Notes

  1. ↑ A. Kelly and K. M. Knowles, Crystallography and Crystal Defects, John Wiley & Sons, Ltd., Chichester, 2nd ed., 2012, ch. 9, pp. 269–304.
  2. 1 2 3 4 5 6 Hertzberg, Richard W.; Vinci, Richard P.; Hertzberg, Jason L. (2013). Deformation and Fracture Mechanics of Engineering Materials. John Wiley & Sons, Inc. p. 80. ISBN 978-0-470-52780-1.
  3. ↑ Luc Remy. PhD thesis, Universite de Paris-Sud, Orsay, France, 1975.
  4. 1 2 3 4 Venables, J. A. (1964). The electron microscopy of deformation twinning. Journal of Physics and Chemistry of Solids, 25, 685–690.
  5. 1 2 3 Zhao, Y.H., Liao, Y.Y., Zhu, Y.T. (2005). Influence of stacking fault energy on nanostructure under high pressure torsion. Materials Science and Engineering A, 410–411, 188–193.
  6. ↑ N.V. Ravi Kumar et al., Grain refinement in AZ91 magnesium alloy during thermomechanical processing, Materials and Engineering A359 (2003), 150–157.
  7. ↑ Lawrence E. Murr. Interfacial Phenomena in Metals and Alloys. Addison-Wesley Pub. Co., 1975.
  8. 1 2 3 Rohatgi, A., Vecchio, K., Gray, G., (2001). The influence of stacking fault energy on the mechanical behavior of Cu and Cu-Al alloy: Deformation twinning, work hardening, and dynamic recovery. Metallurgical and Materials Transactions A 32A, 135–145.
  9. 1 2 Johari, O., Thomas, G., (1964). Substrates in explosively deformed Cu and Cu-Al alloys. Acta Metallurgica 12, (10), 1153–1159.
  10. 1 2 Thornton, P. R., Mitchell, T.E., Hirsch, P.B., (1962). The dependence of cross-slip on stacking fault energy in face centered cubic metals and alloys. Philosophical Magazine, 7, (80), 1349–1369.
  11. ↑ El-Danaf, E., (2012). Mechanical properties, microstructure and micro-texture evolution for 1050AA deformed by equal channel angular pressing (ECAP) and post ECAP plane strain compression using two loading schemes. Materials and Design, 34, 793-807.
  12. 1 2 3 Dillamore, I., Butler, E., Green, D., (1968). Crystal rotations under conditions of imposed strain and the influence of twinning and cross-slip. Metal Science Journal, 2 (1), 161–167.
  13. 1 2 Groves, G., Kelly, A., (1963). Independent slip systems in crystals. Philosophical Magazine, 8 (89), 877–887.
  14. 1 2 Smallman, R., Green, D., (1964). The dependence of rolling texture on stacking fault energy. Acta Metallurgica, 12 (2), 145-154.
  15. ↑ Heye, W., Wassermann, G., (1966). Mechanical twinning in cold-rolled silver crystals. Physica Status Solidi, 18 (2), K107–K111.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.