In mathematics, stochastic analysis on manifolds or stochastic differential geometry is the study of stochastic analysis over smooth manifolds. It is therefore a synthesis of stochastic analysis and differential geometry.
The connection between analysis and stochastic processes stems from the fundamental relation that the infinitesimal generator of a continuous strong Markov process is a second-order elliptic operator. The infinitesimal generator of Brownian motion is the Laplace operator and the transition probability density of Brownian motion is the minimal heat kernel of the heat equation. Interpreting the paths of Brownian motion as characteristic curves of the operator, Brownian motion can be seen as a stochastic counterpart of a flow to a second-order partial differential operator.
Stochastic analysis on manifolds investigates stochastic processes on non-linear state spaces or manifolds. Classical theory can be reformulated in a coordinate-free representation. In that, it is often complicated (or not possible) to formulate objects with coordinates of . Thus, we require an additional structure in form of a linear connection or Riemannian metric to define martingales and Brownian motion on manifolds. Therefore, controlled by the Riemannian metric, Brownian motion will be a local object by definition. However, its stochastic behaviour determines global aspects of the topology and geometry of the manifold.
Brownian motion is defined to be the diffusion process generated by the Laplace-Beltrami operator with respect to a manifold and can be constructed as the solution to a non-canonical stochastic differential equation on a Riemannian manifold. As there is no Hörmander representation of the operator if the manifold is not parallelizable, i.e. if the tangent bundle is not trivial, there is no canonical procedure to construct Brownian motion. However, this obstacle can be overcome if the manifold is equipped with a connection: We can then introduce the stochastic horizontal lift of a semimartingale and the stochastic development by the so-called Eells-Elworthy-Malliavin construction.[1][2]
The latter is a generalisation of a horizontal lift of smooth curves to horizontal curves in the frame bundle, such that the anti-development and the horizontal lift are connected by a stochastic differential equation. Using this, we can consider an SDE on the orthonormal frame bundle of a Riemannian manifold, whose solution is Brownian motion, and projects down to the (base) manifold via stochastic development. A visual representation of this construction corresponds to the construction of a spherical Brownian motion by rolling without slipping the manifold along the paths (or footprints) of Brownian motion left in Euclidean space.[3]
Stochastic differential geometry provides insight into classical analytic problems, and offers new approaches to prove results by means of probability. For example, one can apply Brownian motion to the Dirichlet problem at infinity for Cartan-Hadamard manifolds[4] or give a probabilistic proof of the Atiyah-Singer index theorem.[5] Stochastic differential geometry also applies in other areas of mathematics (e.g. mathematical finance). For example, we can convert classical arbitrage theory into differential-geometric language (also called geometric arbitrage theory).[6]
Preface
For the reader's convenience and if not stated otherwise, let be a filtered probability space and be a smooth manifold. The filtration satisfies the usual conditions, i.e. it is right-continuous and complete. We use the Stratonovich integral which obeys the classical chain rule (compared to Itô calculus). The main advantage for us lies in the fact that stochastic differential equations are then stable under diffeomorphisms between manifolds, i.e. if is a solution, then also is a solution under transformations of the stochastic differential equation.
Notation:
- is. the tangent bundle of .
- is the cotangent bundle of .
- is the -module of vector fields on .
- is the Stratonovich integral.
- is the space of test functions on , i.e. is smooth and has compact support.
- is the one-point compactification (or Alexandroff compactification).
Flow processes
Flow processes (also called -diffusions) are the probabilistic counterpart of integral curves (flow lines) of vector fields. In contrast, a flow process is defined with respect to a second-order differential operator, and thus, generalises the notion of deterministic flows being defined with respect to a first-order operator.
Partial differential operator in Hörmander form
Let be a vector field, understood as a derivation by the -isomorphism
for some . The map is defined by . For the composition, we set for some .
A partial differential operator (PDO) is given in Hörmander form if and only there are vector fields and can be written in the form
- .
Flow process
Let be a PDO in Hörmander form on and a starting point. An adapted and continuous -valued process with is called a flow process to starting in , if for every test function and the process
is a martingale, i.e.
- .
Remark
For a test function , a PDO in Hörmander form and a flow process (starting in ) also holds the flow equation, but in comparison to the deterministic case only in mean
- .
and we can recover the PDO by taking the time derivative at time 0, i.e.
- .
Lifetime and explosion time
Let be open und a predictable stopping time. We call the lifetime of a continuous semimartingale on if
- there is a sequence of stopping times with , such that -almost surely on .
- the stopped process is a semimartingale.
Moreover, if for almost all , we call explosion time.
A flow process can have a finite lifetime . By this we mean that is defined such that if , then -almost surely on we have in the one-point compactification . In that case we extend the process path-wise by for .
Semimartingales on a manifold
A process is a semimartingale on , if for every the random variable is an -semimartingale, i.e. the composition of any smooth function with the process is a real-valued semimartingale. It can be shown that any -semimartingale is a solution of a stochastic differential equation on . If the semimartingale is only defined up to a finite lifetime , we can always construct a semimartingale with infinite lifetime by a transformation of time. A semimartingale has a quadratic variation with respect to a section in the bundle of bilinear forms on .
Introducing the Stratonovich Integral of a differential form along the semimartingale we can study the so called winding behaviour of , i.e. a generalisation of the winding number.
Stratonovich integral of a 1-form
Let be an -valued semimartingale and be a 1-form. We call the integral the Stratonovich integral of along . For we define .
SDEs on a manifold
A stochastic differential equation on a manifold , denoted SDE on , is defined by the pair including a bundle homomorphism (i.e. a homomorphism of vector bundles) or the ()-tuple with vector fields given. Using the Whitney embedding, we can show that there is a unique maximal solution to every SDE on with initial condition . If we have identified the maximal solution, we recover directly a flow process to the operator .
Definition
An SDE on is a pair , where
- is a continuous semimartingale on a finite-dimensional -vector space ; and
- is a (smooth) homomorphism of vector bundles over
where is a linear map.
The stochastic differential equation is denoted by
or
The latter follows from setting with respect to a basis and -valued semimartingales with .
As for given vector fields there is exactly one bundle homomorphism such that , our definition of an SDE on as is plausible.
If has only finite life time, we can transform the time horizon into the infinite case.[7]
Solutions
Let be an SDE on and an -measurable random variable. Let be a continuous adapted -valued process with life time on the same probability space such as . Then is called a solution to the SDE
with initial condition up to the life time , if for every test function the process is an -valued semimartingale and for every stopping time with , it holds -almost surely
- ,
where is the push-forward (or differential) at the point . Following the idea from above, by definition is a semimartingale for every test function , so that is a semimartingale on .
If the lifetime is maximal, i.e.
-almost surely, we call this solution the maximal solution. The lifetime of a maximal solution can be extended to all of , and after extending to the whole of , the equation
- ,
holdsup to indistinguishability.[8]
Remark
Let with a -dimensional Brownian motion , then we can show that every maximal solution starting in is a flow process to the operator
- .
Martingales and Brownian motion
Brownian motion on manifolds are stochastic flow processes to the Laplace-Beltrami operator. It is possible to construct Brownian motion on Riemannian manifolds . However, to follow a canonical ansatz, we need some additional structure. Let be the orthogonal group; we consider the canonical SDE on the orthonormal frame bundle over , whose solution is Brownian motion. The orthonormal frame bundle is the collection of all sets of orthonormal frames of the tangent space
or in other words, the -principal bundle associated to .
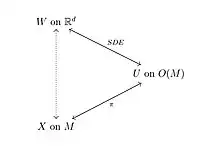
Let be an -valued semimartingale. The solution of the SDE
defined by the projection of a Brownian motion on the Riemannian manifold, is the stochastic development from on . Conversely we call the anti-development of or, respectively, . In short, we get the following relations: , where
- is an -valued semimartingale; and
- is an -valued semimartingale.
For a Riemannian manifold we always use the Levi-Civita connection and the corresponding Laplace-Beltrami operator . The key observation is that there exists a lifted version of the Laplace-Beltrami operator on the orthonormal frame bundle. The fundamental relation reads, for ,
for all with , and the operator on is well-defined for so-called horizontal vector fields. The operator is called Bochner's horizontal Laplace operator.
Martingales with linear connection
To define martingales, we need a linear connection . Using the connection, we can characterise -martingales, if their anti-development is a local martingale. It is also possible to define -martingales without using the anti-development.
We write to indicate that equality holds modulo differentials of local martingales.
Let be an -valued semimartingale. Then is a martingale or -martingale, if and only if for every , it holds that
Brownian motion on a Riemannian manifold
Let be a Riemannian manifold with Laplace-Beltrami operator . An adapted -valued process with maximal lifetime is called a Brownian motion, if for every
is a local -martingale with life time . Hence, Brownian motion Bewegung is the diffusion process to . Note that this characterisation does not provide a canonical procedure to define Brownian motion.
References and notes
- ↑ Stochastic differential equations on manifolds. Vol. 70. 1982.
- ↑ Géométrie différentielle stochastique. 1978.
- ↑ Stochastische Analysis: Eine Einführung in die Theorie der stetigen Semimartingale. pp. 349–544. ISBN 978-3-519-02229-9.
- ↑ Brownian Motion and the Dirichlet Problem at Infinity on Two-dimensional Cartan-Hadamard Manifolds. Vol. 41. 2014. pp. 443–462. doi:10.1007/s11118-013-9376-3.
- ↑ Stochastic Analysis on Manifolds. Vol. 38.
- ↑ Geometric Arbitrage Theory and Market Dynamics. Vol. 7. 2015. doi:10.3934/jgm.2015.7.431.
- ↑ Stochastische Analysis: Eine Einführung in die Theorie der stetigen Semimartingale. p. 364. ISBN 978-3-519-02229-9.
- ↑ Wolfgang Hackenbroch und Anton Thalmaier, Vieweg+Teubner Verlag Wiesbaden (ed.), Stochastische Analysis: Eine Einführung in die Theorie der stetigen Semimartingale, p. 364, ISBN 978-3-519-02229-9
Bibliography
- Wolfgang Hackenbroch und Anton Thalmaier, Vieweg+Teubner Verlag Wiesbaden (ed.), Stochastische Analysis: Eine Einführung in die Theorie der stetigen Semimartingale [Stochastic Analysis: An introduction to the theory of continuous semimartingales], pp. 349–544, ISBN 978-3-519-02229-9
- Nobuyuki Ikeda und Shinzo Watanabe, North Holland (ed.), Stochastic Differential Equations and Diffusion Processes
- Elton P. Hsu, American Mathematical Society (ed.), "Stochastic Analysis on Manifolds", Graduate Studies in Mathematics, vol. 38
- K. D. Elworthy (1982), Cambridge University Press (ed.), Stochastic Differential Equations on Manifolds, doi:10.1017/CBO9781107325609