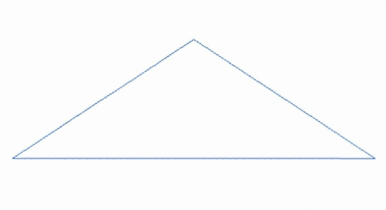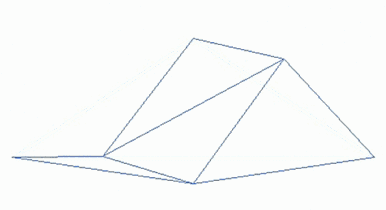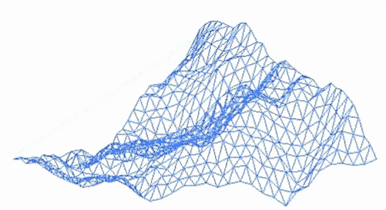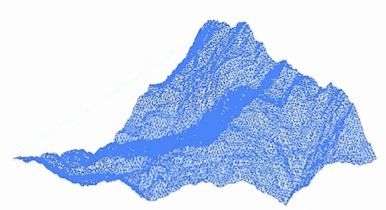
Use of triangular fractals to create a mountainous terrain.

A fractal landscape or fractal surface is generated using a stochastic algorithm designed to produce fractal behavior that mimics the appearance of natural terrain. In other words, the surface resulting from the procedure is not a deterministic, but rather a random surface that exhibits fractal behavior.[1]

Many natural phenomena exhibit some form of statistical self-similarity that can be modeled by fractal surfaces.[2] Moreover, variations in surface texture provide important visual cues to the orientation and slopes of surfaces, and the use of almost self-similar fractal patterns can help create natural looking visual effects.[3] The modeling of the Earth's rough surfaces via fractional Brownian motion was first proposed by Benoit Mandelbrot.[4]

Because the intended result of the process is to produce a landscape, rather than a mathematical function, processes are frequently applied to such landscapes that may affect the stationarity and even the overall fractal behavior of such a surface, in the interests of producing a more convincing landscape.

According to R. R. Shearer, the generation of natural looking surfaces and landscapes was a major turning point in art history, where the distinction between geometric, computer generated images and natural, man made art became blurred.[5] The first use of a fractal-generated landscape in a film was in 1982 for the movie Star Trek II: The Wrath of Khan. Loren Carpenter refined the techniques of Mandelbrot to create an alien landscape.[6]

Behavior of natural landscapes

A fractal landscape rendered in Terragen.
Computer generated fractal terrain using Perlin noise with Adobe Photoshop and Terragen.
Computer-generated fractal wooded hills using Visual Nature Studio.

Whether or not natural landscapes behave in a generally fractal manner has been the subject of some research. Technically speaking, any surface in three-dimensional space has a topological dimension of 2, and therefore any fractal surface in three-dimensional space has a Hausdorff dimension between 2 and 3.[7] Real landscapes however, have varying behavior at different scales. This means that an attempt to calculate the 'overall' fractal dimension of a real landscape can result in measures of negative fractal dimension, or of fractal dimension above 3. In particular, many studies of natural phenomena, even those commonly thought to exhibit fractal behavior, do not do so over more than a few orders of magnitude. For instance, Richardson's examination of the western coastline of Britain showed fractal behavior of the coastline over only two orders of magnitude.[8] In general, there is no reason to suppose that the geological processes that shape terrain on large scales (for example plate tectonics) exhibit the same mathematical behavior as those that shape terrain on smaller scales (for instance, soil creep).

Real landscapes also have varying statistical behavior from place to place, so for example sandy beaches don't exhibit the same fractal properties as mountain ranges. A fractal function, however, is statistically stationary, meaning that its bulk statistical properties are the same everywhere. Thus, any real approach to modeling landscapes requires the ability to modulate fractal behavior spatially. Additionally, real landscapes have very few natural minima (most of these are lakes), whereas a fractal function has as many minima as maxima, on average. Real landscapes also have features originating with the flow of water and ice over their surface, which simple fractals cannot model.[9]

It is because of these considerations that the simple fractal functions are often inappropriate for modeling landscapes. More sophisticated techniques (known as 'multi-fractal' techniques) use different fractal dimensions for different scales, and thus can better model the frequency spectrum behavior of real landscapes[10]

Generation of fractal landscapes

A way to make such a landscape is to employ the random midpoint displacement algorithm, in which a square is subdivided into four smaller equal squares and the center point is vertically offset by some random amount. The process is repeated on the four new squares, and so on, until the desired level of detail is reached. There are many fractal procedures (such as combining multiple octaves of Simplex noise) capable of creating terrain data, however, the term "fractal landscape" has become more generic over time.

Fractal plants

Fractal plants can be procedurally generated using L-systems in computer-generated scenes.[11]

See also

Notes

  1. ↑ "The Fractal Geometry of Nature".
  2. ↑ Advances in multimedia modeling: 13th International Multimedia Modeling by Tat-Jen Cham 2007 ISBN 3-540-69428-5 page
  3. ↑ Human symmetry perception and its computational analysis by Christopher W. Tyler 2002 ISBN 0-8058-4395-7 pages 173–177
  4. ↑ Dynamics of Fractal Surfaces by Fereydoon Family and Tamas Vicsek 1991 ISBN 981-02-0720-4 page 45
  5. ↑ Rhonda Roland Shearer "Rethinking Images and Metaphors" in The languages of the brain by Albert M. Galaburda 2002 ISBN 0-674-00772-7 pages 351–359
  6. ↑ Briggs, John (1992). Fractals: The Patterns of Chaos : a New Aesthetic of Art, Science, and Nature. Simon and Schuster. p. 84. ISBN 978-0671742171. Retrieved 15 June 2014.
  7. ↑ Lewis
  8. ↑ Richardson
  9. ↑ Ken Musgrave, 1993
  10. ↑ Joost van Lawick van Pabst et al.
  11. ↑ de la Re, Armando; Abad, Francisco; Camahort, Emilio; Juan, M. C. (2009). "Tools for Procedural Generation of Plants in Virtual Scenes" (PDF). Computational Science – ICCS 2009. Lecture Notes in Computer Science. Vol. 5545. pp. 801–810. doi:10.1007/978-3-642-01973-9_89. ISBN 978-3-642-01972-2. S2CID 33892094.

References

  • A Web-Wide World by Ken Perlin, 1998; a Java applet showing a sphere with a generated landscape.


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.