In category theory, a strong monad over a monoidal category (C, ⊗, I) is a monad (T, η, μ) together with a natural transformation t_A,B : A ⊗ TB → T(A ⊗ B), called (tensorial) strength, such that the diagrams

, ,

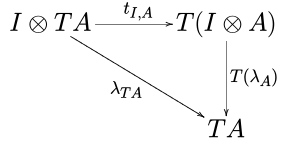, and

commute for every object A, B and C (see Definition 3.2 in ^[1]).

If the monoidal category (C, ⊗, I) is closed then a strong monad is the same thing as a C-enriched monad.

Commutative strong monads

For every strong monad T on a symmetric monoidal category, a costrength natural transformation can be defined by

${\displaystyle t'_{A,B}=T(\gamma _{B,A})\circ t_{B,A}\circ \gamma _{TA,B}:TA\otimes B\to T(A\otimes B)}$.

A strong monad T is said to be commutative when the diagram

commutes for all objects ${\displaystyle A}$ and ${\displaystyle B}$.^[2]

One interesting fact about commutative strong monads is that they are "the same as" symmetric monoidal monads. More explicitly,

• a commutative strong monad ${\displaystyle (T,\eta ,\mu ,t)}$ defines a symmetric monoidal monad ${\displaystyle (T,\eta ,\mu ,m)}$ by

${\displaystyle m_{A,B}=\mu _{A\otimes B}\circ Tt'_{A,B}\circ t_{TA,B}:TA\otimes TB\to T(A\otimes B)}$

• and conversely a symmetric monoidal monad ${\displaystyle (T,\eta ,\mu ,m)}$ defines a commutative strong monad ${\displaystyle (T,\eta ,\mu ,t)}$ by

${\displaystyle t_{A,B}=m_{A,B}\circ (\eta _{A}\otimes 1_{TB}):A\otimes TB\to T(A\otimes B)}$

and the conversion between one and the other presentation is bijective.

References

• Anders Kock (1972). "Strong functors and monoidal monads" (PDF). Archiv der Mathematik. 23: 113–120. doi:10.1007/BF01304852. S2CID 13246783.
• Jean Goubault-Larrecq, Slawomir Lasota and David Nowak (2005). "Logical Relations for Monadic Types". Mathematical Structures in Computer Science. 18 (6): 1169. arXiv:cs/0511006. doi:10.1017/S0960129508007172. S2CID 741758.