The volumetric heat capacity of a material is the heat capacity of a sample of the substance divided by the volume of the sample. It is the amount of energy that must be added, in the form of heat, to one unit of volume of the material in order to cause an increase of one unit in its temperature. The SI unit of volumetric heat capacity is joule per kelvin per cubic meter, J⋅K−1⋅m−3.
The volumetric heat capacity can also be expressed as the specific heat capacity (heat capacity per unit of mass, in J⋅K−1⋅kg−1) times the density of the substance (in kg/L, or g/mL).[1]
This quantity may be convenient for materials that are commonly measured by volume rather than mass, as is often the case in engineering and other technical disciplines. The volumetric heat capacity often varies with temperature, and is different for each state of matter. While the substance is undergoing a phase transition, such as melting or boiling, its volumetric heat capacity is technically infinite, because the heat goes into changing its state rather than raising its temperature.
The volumetric heat capacity of a substance, especially a gas, may be significantly higher when it is allowed to expand as it is heated (volumetric heat capacity at constant pressure) than when is heated in a closed vessel that prevents expansion (volumetric heat capacity at constant volume).
If the amount of substance is taken to be the number of moles in the sample (as is sometimes done in chemistry), one gets the molar heat capacity (whose SI unit is joule per kelvin per mole, J⋅K−1⋅mol−1).
Definition
The volumetric heat capacity is defined as
where is the volume of the sample at temperature , and is the amount of heat energy needed to raise the temperature of the sample from to . This parameter is an intensive property of the substance.
Since both the heat capacity of an object and its volume may vary with temperature, in unrelated ways, the volumetric heat capacity is usually a function of temperature too. It is equal to the specific heat of the substance times its density (mass per volume) , both measured at the temperature . Its SI unit is joule per kelvin per cubic meter (J⋅K−1⋅m−3).
This quantity is used almost exclusively for liquids and solids, since for gases it may be confused with the "specific heat capacity at constant volume", which generally has very different values. International standards now recommend that "specific heat capacity" always refer to capacity per unit of mass.[2] Therefore, the word "volumetric" should always be used for this quantity.
History
Dulong and Petit predicted in 1818 that the product of solid substance density and specific heat capacity (ρcp) would be constant for all solids. This amounted to a prediction that volumetric heat capacity in solids would be constant. In 1819 they found that volumetric heat capacities were not quite constant, but that the most constant quantity was the heat capacity of solids adjusted by the presumed weight of the atoms of the substance, as defined by Dalton (the Dulong–Petit law). This quantity was proportional to the heat capacity per atomic weight (or per molar mass), which suggested that it is the heat capacity per atom (not per unit of volume) which is closest to being a constant in solids.
Eventually it became clear that heat capacities per particle for all substances in all states are the same, to within a factor of two, so long as temperatures are not in the cryogenic range.
Typical values
The volumetric heat capacity of solid materials at room temperatures and above varies widely, from about 1.2 MJ⋅K−1⋅m−3 (for example bismuth[3]) to 3.4 MJ⋅K−1⋅m−3 (for example iron[4]). This is mostly due to differences in the physical size of atoms. Atoms vary greatly in density, with the heaviest often being more dense, and thus are closer to taking up the same average volume in solids than their mass alone would predict. If all atoms were the same size, molar and volumetric heat capacity would be proportional and differ by only a single constant reflecting ratios of the atomic molar volume of materials (their atomic density). An additional factor for all types of specific heat capacities (including molar specific heats) then further reflects degrees of freedom available to the atoms composing the substance, at various temperatures.
For most liquids, the volumetric heat capacity is narrower, for example octane at 1.64 MJ⋅K−1⋅m−3 or ethanol at 1.9. This reflects the modest loss of degrees of freedom for particles in liquids as compared with solids.
However, water has a very high volumetric heat capacity, at 4.18 MJ⋅K−1⋅m−3, and ammonia is also fairly high: 3.3 MJ⋅K−1⋅m−3.
For gases at room temperature, the range of volumetric heat capacities per atom (not per molecule) only varies between different gases by a small factor less than two, because every ideal gas has the same molar volume. Thus, each gas molecule occupies the same mean volume in all ideal gases, regardless of the type of gas (see kinetic theory). This fact gives each gas molecule the same effective "volume" in all ideal gases (although this volume/molecule in gases is far larger than molecules occupy on average in solids or liquids). Thus, in the limit of ideal gas behavior (which many gases approximate except at low temperatures and/or extremes of pressure) this property reduces differences in gas volumetric heat capacity to simple differences in the heat capacities of individual molecules. As noted, these differ by a factor depending on the degrees of freedom available to particles within the molecules.
Volumetric heat capacity of gases
Large complex gas molecules may have high heat capacities per mole (of molecules), but their heat capacities per mole of atoms are very similar to those of liquids and solids, again differing by less than a factor of two per mole of atoms. This factor of two represents vibrational degrees of freedom available in solids vs. gas molecules of various complexities.
In monatomic gases (like argon) at room temperature and constant volume, volumetric heat capacities are all very close to 0.5 kJ⋅K−1⋅m−3, which is the same as the theoretical value of 3/2RT per kelvin per mole of gas molecules (where R is the gas constant and T is temperature). As noted, the much lower values for gas heat capacity in terms of volume as compared with solids (although more comparable per mole, see below) results mostly from the fact that gases under standard conditions consist of mostly empty space (about 99.9% of volume), which is not filled by the atomic volumes of the atoms in the gas. Since the molar volume of gases is very roughly 1000 times that of solids and liquids, this results in a factor of about 1000 loss in volumetric heat capacity for gases, as compared with liquids and solids. Monatomic gas heat capacities per atom (not per molecule) are decreased by a factor of 2 with regard to solids, due to loss of half of the potential degrees of freedom per atom for storing energy in a monatomic gas, as compared with regard to an ideal solid. There is some difference in the heat capacity of monatomic vs. polyatomic gasses, and also gas heat capacity is temperature-dependent in many ranges for polyatomic gases; these factors act to modestly (up to the discussed factor of 2) increase heat capacity per atom in polyatomic gases, as compared with monatomic gases. Volumetric heat capacities in polyatomic gases vary widely, however, since they are dependent largely on the number of atoms per molecule in the gas, which in turn determines the total number of atoms per volume in the gas.
The volumetric heat capacity is defined as having SI units of J/(m3⋅K). It can also be described in Imperial units of BTU/(ft3⋅°F).
Volumetric heat capacity of solids
Since the bulk density of a solid chemical element is strongly related to its molar mass (usually about 3R per mole, as noted above), there exists noticeable inverse correlation between a solid's density and its specific heat capacity on a per-mass basis. This is due to a very approximate tendency of atoms of most elements to be about the same size, despite much wider variations in density and atomic weight. These two factors (constancy of atomic volume and constancy of mole-specific heat capacity) result in a good correlation between the volume of any given solid chemical element and its total heat capacity. Another way of stating this, is that the volume-specific heat capacity (volumetric heat capacity) of solid elements is roughly a constant. The molar volume of solid elements is very roughly constant, and (even more reliably) so also is the molar heat capacity for most solid substances. These two factors determine the volumetric heat capacity, which as a bulk property may be striking in consistency. For example, the element uranium is a metal which has a density almost 36 times that of the metal lithium, but uranium's volumetric heat capacity is only about 20% larger than lithium's.
Since the volume-specific corollary of the Dulong–Petit specific heat capacity relationship requires that atoms of all elements take up (on average) the same volume in solids, there are many departures from it, with most of these due to variations in atomic size. For instance, arsenic, which is only 14.5% less dense than antimony, has nearly 59% more specific heat capacity on a mass basis. In other words; even though an ingot of arsenic is only about 17% larger than an antimony one of the same mass, it absorbs about 59% more heat for a given temperature rise. The heat capacity ratios of the two substances closely follows the ratios of their molar volumes (the ratios of numbers of atoms in the same volume of each substance); the departure from the correlation to simple volumes in this case is due to lighter arsenic atoms being significantly more closely packed than antimony atoms, instead of similar size. In other words, similar-sized atoms would cause a mole of arsenic to be 63% larger than a mole of antimony, with a correspondingly lower density, allowing its volume to more closely mirror its heat capacity behavior.
Thermal inertia
Thermal inertia is a term commonly used to describe the observed delays in a body's temperature response during heat transfers. The phenomenon exists because of a body's ability to both store and transport heat relative to its environment. Since the configuration of system components and mix of heat transfer mechanisms (e.g. conduction, convection, radiation, phase change) varies substantially between instances, there is no generally applicable mathematical definition for thermal inertia.[5] The phenomenon occurs in conjunction with a material's or a transport medium's heat transfer properties. A larger thermal storage capacity typically yields a more sluggish temperature response.
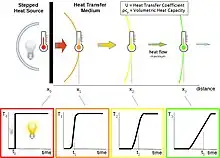
A system containing one or more components with large volumetric heat capacity indicates that dynamic, or transient, effects must be considered when modelling system behavior. Steady-state calculations, many of which produce valid estimates of equilibrium heat flows and temperatures without an accounting for thermal inertia, nevertheless yield no information on the pace of changes between equilibrium states. Response times for complex systems can be evaluated with detailed numerical simulation, or a thermal time constant estimated from a lumped system analysis.[6][7]: 627 A higher value of volumetric heat capacity generally means a longer time for the system to reach equilibrium.
Analogies of thermal inertia to the inertial behaviors observed in other disciplines of engineering and physics can sometimes be used with caution.[8] In building design, thermal inertia is also known as the thermal flywheel effect, and a thermal mass can produce a delay between diurnal heat flow and temperature which is similar to the delay between current and voltage in an AC-driven RC circuit. Thermal inertia is less directly comparable to the mass-and-velocity term used in mechanics, where inertia restricts the acceleration of an object. In a similar way, thermal inertia is a measure of the thermal mass and the velocity of the thermal wave which controls the surface temperature of a material.
Thermal effusivity
For a semi-infinite rigid body where heat transfer is dominated by the diffusive process of conduction only, thermal inertia can be approximated from the material's thermal effusivity (e). It is defined as the square root of the product of the material's bulk thermal conductivity and volumetric heat capacity, where the latter is the product of density and specific heat capacity:[9][10]
- is thermal conductivity, with unit W⋅m−1⋅K−1
- is density, with unit kg⋅m−3
- is specific heat capacity, with unit J⋅kg−1⋅K−1
- has SI units of thermal inertia of J⋅m−2⋅K−1⋅s−1/2. Non-SI units of kieffers: Cal⋅cm−2⋅K−1⋅s−1/2, are also used informally in older references.[lower-roman 1]
Constant volume and constant pressure
For gases it is necessary to distinguish between volumetric heat capacity at constant volume and volumetric heat capacity at constant pressure, which is always larger due to the pressure–volume work done as a gas expands during heating at constant pressure (thus absorbing heat which is converted to work). The distinctions between constant-volume and constant-pressure heat capacities are also made in various types of specific heat capacity (the latter meaning either mass-specific or mole-specific heat capacity).
See also
References
- ↑ Coined by the planetary geophysicist Hugh H. Kieffer.
- ↑ U.S. Army Corps of Engineers Technical Manual: Arctic and Subarctic Construction: Calculation Methods for Determination of Depths of Freeze and Thaw in Soils, TM 5-852-6/AFR 88-19, Volume 6, 1988, Equation 2-1
- ↑ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), ISBN 92-822-2213-6, archived (PDF) from the original on 2021-06-04, retrieved 2021-12-16
- ↑ Based on values in this table and density.
- ↑ Based on NIST data and density.
- ↑ Sala-Lizarraga, Jose; Picallo-Perez, Ana (2019). Exergy Analysis and Thermoeconomics of Buildings. Elsevier. pp. 272–273. doi:10.1016/B978-0-12-817611-5.00004-7. ISBN 9780128176115. S2CID 210737476.
- ↑ Keshavarz, P.; Taheri, M. (2007). "An improved lumped analysis for transient heat conduction by using the polynomial approximation method". Heat and Mass Transfer. 43: 1151–1156. doi:10.1007/s00231-006-0200-0.
- ↑ Gerald R. North (1988). "Lessons from energy balance models". In Michael E. Schlesinger (ed.). Physically-based Modelling and Simulation of Climate and Climatic Change (NATO Advanced Study Institute on Physical-Based Modelling ed.). Springer. NATO. ISBN 978-90-277-2789-3.
- ↑ Veto, M.S.; Christensen, P.R. (2015). "Mathematical Theory of Thermal Inertia Revisited" (PDF). 46th Lunar and Planetary Science Conference.
- ↑ Dante, Roberto C. (2016). Handbook of Friction Materials and Their Applications. Elsevier. pp. 123–134. doi:10.1016/B978-0-08-100619-1.00009-2.
- ↑ Carslaw, H.S.; Jaeger, J.C. (1959). Conduction of Heat in Solids. Clarendon Press, Oxford. ISBN 978-0-19-853368-9.