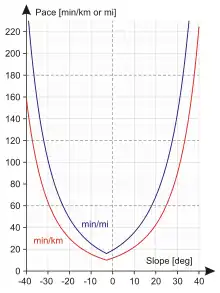
Tobler's hiking function – walking speed vs. slope angle chart.
Tobler's hiking function is an exponential function determining the hiking speed, taking into account the slope angle.[1][2][3] It was formulated by Waldo Tobler. This function was estimated from empirical data of Eduard Imhof.[4]
Formula
Walking velocity:
where
- W = walking velocity [km/h][2]
- dh = elevation difference,
- dx = distance,
- S = slope,
- θ = angle of slope (inclination).
The velocity on the flat terrain is 5 km / h, the maximum speed of 6 km / h is achieved roughly at -2.86°.[5]
On flat terrain this formula works out to 5 km/h. For off-path travel, this value should be multiplied by 3/5, for horseback by 5/4.[1]
Pace
Pace is the reciprocal of speed.[6][7] For Tobler's hiking function it can be calculated from the following conversion:[7]
where
- p = pace [s/m]
- m = gradient uphill or downhill (dh/dx = S in Tobler's formula),
Sample values
| Slope (deg) | Gradient (dh/dx) | Speed | Pace | |||
|---|---|---|---|---|---|---|
| km / h | mi / h | min / km | min / mi | s / m | ||
| -60 | -1.73 | 0.02 | 0.01 | 3603.9 | 5799.9 | 216.23 |
| -50 | -1.19 | 0.11 | 0.07 | 543.9 | 875.3 | 32.63 |
| -40 | -0.84 | 0.38 | 0.24 | 158.3 | 254.7 | 9.50 |
| -30 | -0.58 | 0.95 | 0.59 | 63.3 | 101.9 | 3.80 |
| -25 | -0.47 | 1.40 | 0.87 | 42.9 | 69.1 | 2.58 |
| -20 | -0.36 | 2.00 | 1.24 | 30.0 | 48.3 | 1.80 |
| -15 | -0.27 | 2.80 | 1.74 | 21.4 | 34.5 | 1.29 |
| -10 | -0.18 | 3.86 | 2.40 | 15.6 | 25.0 | 0.93 |
| -5 | -0.09 | 5.26 | 3.27 | 11.4 | 18.3 | 0.68 |
| -2.8624 | -0.05 | 6.00 | 3.73 | 10.0 | 16.1 | 0.60 |
| 0 | 0 | 5.04 | 3.13 | 11.9 | 19.2 | 0.71 |
| 1 | 0.02 | 4.74 | 2.94 | 12.7 | 20.4 | 0.76 |
| 5 | 0.09 | 3.71 | 2.30 | 16.2 | 26.0 | 0.97 |
| 10 | 0.18 | 2.72 | 1.69 | 22.1 | 35.5 | 1.32 |
| 15 | 0.27 | 1.97 | 1.23 | 30.4 | 49.0 | 1.83 |
| 20 | 0.36 | 1.41 | 0.88 | 42.6 | 68.5 | 2.56 |
| 25 | 0.47 | 0.98 | 0.61 | 60.9 | 98.1 | 3.66 |
| 30 | 0.58 | 0.67 | 0.41 | 89.9 | 144.6 | 5.39 |
| 40 | 0.84 | 0.27 | 0.17 | 224.6 | 361.5 | 13.48 |
| 50 | 1.19 | 0.08 | 0.05 | 771.8 | 1242.1 | 46.31 |
See also
References
- 1 2 Tobler, Waldo (February 1993). "Three presentations on geographical analysis and modeling: Non-isotropic geographic modeling speculations on the geometry of geography global spatial analysis" (PDF). Technical Report. National center for geographic information and analysis. 93 (1). Retrieved 21 March 2013. Available also in HTML format.
- 1 2 Magyari-Sáska, Zsolt; Dombay, Ştefan (2012). "Determining minimum hiking time using DEM" (PDF). Geographia Napocensis. Academia Romana − Filiala Cluj Colectivul de Geografie. Anul VI (2): 124–129. Retrieved 21 March 2013.
- ↑ Kondo, Yasuhisa; Seino, Yoichi (2010). "GPS-aided Walking Experiments and Data-driven Travel Cost Modeling on the Historical Road of Nakasendō-Kisoji (Central Highland Japan)". In Frischer, Bernard (ed.). Making history interactive: computer applications and quantitative methods in archaeology (CAA); proceedings of the 37th international conference, Williamsburg, Virginia, United States of America, March 22−26, 2009. BAR International Series. Oxford u.a.: Archaeopress. pp. 158–165. Retrieved 21 March 2013.
- ↑ Imhof, Eduard (1950). Gelaende und Karte. Rentsch, Zurich.
- ↑ Analyzing Tobler's Hiking Function and Naismith's Rule Using Crowd-Sourced GPS Data. Erik Irtenkauf. The Pennsylvania State University. May 2014
- ↑ Kay, A. (2012). "Route Choice in Hilly Terrain" (PDF). Geogr Anal. 44 (2): 87–108. CiteSeerX 10.1.1.391.1203. doi:10.1111/j.1538-4632.2012.00838.x. Archived from the original (PDF) on 2012-11-14. Retrieved 19 January 2017.
- 1 2 Kay, A. (November 2012). "Pace and critical gradient for hill runners: an analysis of race records" (PDF). Journal of Quantitative Analysis in Sports. 8 (4). doi:10.1515/1559-0410.1456. ISSN 1559-0410. Retrieved 19 January 2017.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.