In numerical methods, total variation diminishing (TVD) is a property of certain discretization schemes used to solve hyperbolic partial differential equations. The most notable application of this method is in computational fluid dynamics. The concept of TVD was introduced by Ami Harten.^[1]

Model equation

In systems described by partial differential equations, such as the following hyperbolic advection equation,

${\displaystyle {\frac {\partial u}{\partial t}}+a{\frac {\partial u}{\partial x}}=0,}$

the total variation (TV) is given by

${\displaystyle TV(u(\cdot ,t))=\int \left|{\frac {\partial u}{\partial x}}\right|\mathrm {d} x,}$

and the total variation for the discrete case is,

${\displaystyle TV(u^{n})=TV(u(\cdot ,t^{n}))=\sum _{j}\left|u_{j+1}^{n}-u_{j}^{n}\right|.}$

where ${\displaystyle u_{j}^{n}=u(x_{j},t^{n})}$.

A numerical method is said to be total variation diminishing (TVD) if,

${\displaystyle TV\left(u^{n+1}\right)\leq TV\left(u^{n}\right).}$

Characteristics

A numerical scheme is said to be monotonicity preserving if the following properties are maintained:

• If ${\displaystyle u^{n}}$ is monotonically increasing (or decreasing) in space, then so is ${\displaystyle u^{n+1}}$.

Harten 1983 proved the following properties for a numerical scheme,

• A monotone scheme is TVD, and
• A TVD scheme is monotonicity preserving.

Application in CFD

In Computational Fluid Dynamics, TVD scheme is employed to capture sharper shock predictions without any misleading oscillations when variation of field variable “${\displaystyle \phi }$” is discontinuous. To capture the variation fine grids (${\displaystyle \Delta x}$ very small) are needed and the computation becomes heavy and therefore uneconomic. The use of coarse grids with central difference scheme, upwind scheme, hybrid difference scheme, and power law scheme gives false shock predictions. TVD scheme enables sharper shock predictions on coarse grids saving computation time and as the scheme preserves monotonicity there are no spurious oscillations in the solution.

Discretisation

Consider the steady state one-dimensional convection diffusion equation,

${\displaystyle \nabla \cdot (\rho \mathbf {u} \phi )\,=\nabla \cdot (\Gamma \nabla \phi )+S_{\phi }\;}$,

where ${\displaystyle \rho }$ is the density, ${\displaystyle \mathbf {u} }$ is the velocity vector, ${\displaystyle \phi }$ is the property being transported, ${\displaystyle \Gamma }$ is the coefficient of diffusion and ${\displaystyle S_{\phi }}$ is the source term responsible for generation of the property ${\displaystyle \phi }$.

Making the flux balance of this property about a control volume we get,

${\displaystyle \int _{A}\mathbf {n} \cdot (\rho \mathbf {u} \phi )\,\mathrm {d} A=\int _{A}\mathbf {n} \cdot (\Gamma \nabla \phi )\,\mathrm {d} A+\int _{CV}S_{\phi }\,\mathrm {d} V}$ ${\displaystyle \;}$

Here ${\displaystyle \mathbf {n} }$ is the normal to the surface of control volume.

Ignoring the source term, the equation further reduces to:

${\displaystyle (\rho \mathbf {u} \phi A)_{r}-(\rho \mathbf {u} \phi A)_{l}=\left(\Gamma A{\frac {\partial \phi }{\partial x}}\right)_{r}-\left(\Gamma A{\frac {\partial \phi }{\partial x}}\right)_{l}}$

A picture showing the control volume with velocities at the faces,nodes and the distance between them, where 'P' is the node at the center.

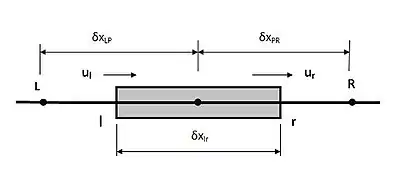
Assuming

${\displaystyle {\frac {\partial \phi }{\partial x}}={\frac {\delta \phi }{\delta x}}}$ and ${\displaystyle A_{r}=A_{l},}$

The equation reduces to

${\displaystyle (\rho \mathbf {u} \phi )_{r}-(\rho \mathbf {u} \phi )_{l}\,=\left({\frac {\Gamma }{\delta x}}\delta \phi \right)_{r}-\left({\frac {\Gamma }{\delta x}}\delta \phi \right)_{l}.}$

Say,

${\displaystyle F_{r}=(\rho \mathbf {u} )_{r};\qquad F_{l}=(\rho \mathbf {u} )_{l};}$

${\displaystyle D_{l}=\left({\frac {\Gamma }{\delta x}}\right)_{l};\qquad D_{r}=\left({\frac {\Gamma }{\delta x}}\right)_{r};}$

From the figure:

${\displaystyle \delta \phi _{r}=\phi _{R}-\phi _{P};\qquad \delta x_{r}=x_{PR};}$

${\displaystyle \delta \phi _{l}=\phi _{P}-\phi _{L};\qquad \delta x_{l}=x_{LP};}$

The equation becomes:

$${\displaystyle F_{r}\phi _{r}-F_{l}\phi _{l}=D_{r}(\phi _{R}-\phi _{P})-D_{l}(\phi _{P}-\phi _{L});}$$

The continuity equation also has to be satisfied in one of its equivalent forms for this problem:

${\displaystyle (\rho \mathbf {u} )_{r}-(\rho \mathbf {u} )_{l}\,=0\ \ \Longleftrightarrow \ \ F_{r}-F_{l}=0\ \ \Longleftrightarrow \ F_{r}=F_{l}=F.}$

Assuming diffusivity is a homogeneous property and equal grid spacing we can say

${\displaystyle \Gamma _{l}=\Gamma _{r};\qquad \delta x_{LP}=\delta x_{PR}=\delta x,}$

we get

$${\displaystyle D_{l}=D_{r}=D.}$$

The equation further reduces to

$${\displaystyle (\phi _{r}-\phi _{l})\cdot F=D\cdot (\phi _{R}-2\phi _{P}+\phi _{L}).}$$

The equation above can be written as

$${\displaystyle (\phi _{r}-\phi _{l})\cdot P=(\phi _{R}-2\phi _{P}+\phi _{L})}$$

where ${\displaystyle P}$ is the Péclet number

${\displaystyle P={\frac {F}{D}}={\frac {\rho \mathbf {u} \delta x}{\Gamma }}.}$

TVD scheme

Total variation diminishing scheme^[2][3] makes an assumption for the values of ${\displaystyle \phi _{r}}$ and ${\displaystyle \phi _{l}}$ to be substituted in the discretized equation as follows:

${\displaystyle \phi _{r}\cdot P={\frac {1}{2}}(P+|P|)[f_{r}^{+}\phi _{R}+(1-f_{r}^{+})\phi _{L}]+{\frac {1}{2}}(P-|P|)[f_{r}^{-}\phi _{P}+(1-f_{r}^{-})\phi _{RR}]}$

${\displaystyle \phi _{l}\cdot P={\frac {1}{2}}(P+|P|)[f_{l}^{+}\phi _{P}+(1-f_{l}^{+})\phi _{LL}]+{\frac {1}{2}}(P-|P|)[f_{l}^{-}\phi _{L}+(1-f_{l}^{-})\phi _{R}]}$

Where ${\displaystyle P}$ is the Péclet number and ${\displaystyle f}$ is the weighing function to be determined from,

${\displaystyle f=f\left({\frac {\phi _{U}-\phi _{UU}}{\phi _{D}-\phi _{UU}}}\right)}$

where ${\displaystyle U}$ refers to upstream, ${\displaystyle UU}$ refers to upstream of ${\displaystyle U}$ and ${\displaystyle D}$ refers to downstream.

Note that ${\displaystyle f^{+}}$ is the weighing function when the flow is in positive direction (i.e., from left to right) and ${\displaystyle f^{-}}$ is the weighing function when the flow is in the negative direction from right to left. So,

${\displaystyle {\begin{aligned}&f_{r}^{+}{\text{ is a function of }}\left({\dfrac {\phi _{P}-\phi _{L}}{\phi _{R}-\phi _{L}}}\right),\\[10pt]&f_{r}^{-}{\text{ is a function of }}\left({\dfrac {\phi _{R}-\phi _{RR}}{\phi _{P}-\phi _{RR}}}\right),\\[10pt]&f_{l}^{+}{\text{ is a function of }}\left({\dfrac {\phi _{L}-\phi _{LL}}{\phi _{P}-\phi _{LL}}}\right),{\text{ and}}\\[10pt]&f_{l}^{-}{\text{ is a function of }}\left({\dfrac {\phi _{P}-\phi _{R}}{\phi _{L}-\phi _{R}}}\right).\end{aligned}}}$

If the flow is in positive direction then, Péclet number ${\displaystyle P}$ is positive and the term ${\displaystyle (P-|P|)=0}$, so the function ${\displaystyle f^{-}}$ won't play any role in the assumption of ${\displaystyle \phi _{r}}$ and ${\displaystyle \phi _{l}}$. Likewise when the flow is in negative direction, ${\displaystyle P}$ is negative and the term ${\displaystyle (P+|P|)=0}$, so the function ${\displaystyle f^{+}}$ won't play any role in the assumption of ${\displaystyle \phi _{r}}$ and ${\displaystyle \phi _{r}}$.

It therefore takes into account the values of property depending on the direction of flow and using the weighted functions tries to achieve monotonicity in the solution thereby producing results with no spurious shocks.

Limitations

Monotone schemes are attractive for solving engineering and scientific problems because they do not produce non-physical solutions. Godunov's theorem proves that linear schemes which preserve monotonicity are, at most, only first order accurate. Higher order linear schemes, although more accurate for smooth solutions, are not TVD and tend to introduce spurious oscillations (wiggles) where discontinuities or shocks arise. To overcome these drawbacks, various high-resolution, non-linear techniques have been developed, often using flux/slope limiters.

See also

• Flux limiters
• Godunov's theorem
• High-resolution scheme
• MUSCL scheme
• Sergei K. Godunov
• Total variation

References

Further reading

• Hirsch, C. (1990), Numerical Computation of Internal and External Flows, Vol 2, Wiley.
• Laney, C. B. (1998), Computational Gas Dynamics, Cambridge University Press.
• Toro, E. F. (1999), Riemann Solvers and Numerical Methods for Fluid Dynamics, Springer-Verlag.
• Tannehill, J. C., Anderson, D. A., and Pletcher, R. H. (1997), Computational Fluid Mechanics and Heat Transfer, 2nd Ed., Taylor & Francis.
• Wesseling, P. (2001), Principles of Computational Fluid Dynamics, Springer-Verlag.
• Anil W. Date Introduction to Computational Fluid Dynamics, Cambridge University Press.