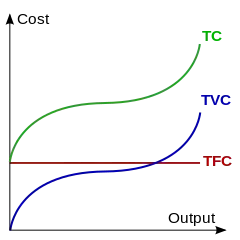
One can decompose total costs as the sum of fixed costs and variable costs. Here output is measured along the horizontal axis. In the Cost-Volume-Profit Analysis model, total costs are linear in volume.
The total cost curve, if non-linear, can represent increasing and diminishing marginal returns.

In economics, total cost (TC) is the minimum financial cost of producing some quantity of output. This is the total economic cost of production and is made up of variable cost, which varies according to the quantity of a good produced and includes inputs such as labor and raw materials, plus fixed cost, which is independent of the quantity of a good produced and includes inputs that cannot be varied in the short term such as buildings and machinery, including possibly sunk costs.

Total cost in economics includes the total opportunity cost (benefits received from the next-best alternative) of each factor of production as part of its fixed or variable costs.

The additional total cost of one additional unit of production is called marginal cost.

The marginal cost can also be calculated by finding the derivative of total cost or variable cost. Either of these derivatives work because the total cost includes variable cost and fixed cost, but fixed cost is a constant with a derivative of 0.

The total cost of producing a specific level of output is the cost of all the factors of production. Often, economists use models with two inputs: physical capital, with quantity K and labor, with quantity L. Capital is assumed to be the fixed input, meaning that the amount of capital used does not vary with the level of production in the short run. The rental price per unit of capital is denoted r. Thus, the total fixed cost equals Kr. Labor is the variable input, meaning that the amount of labor used varies with the level of output. In the short run, the only way to vary output is by varying the amount of the variable input. Labor usage is denoted L and the per unit cost, or wage rate, is denoted w, so the variable cost is Lw. Consequently, total cost is fixed cost (FC) plus variable cost (VC), or TC = FC + VC = Kr+Lw. In the long run, however, both capital usage and labor usage are variable. The long run total cost for a given output will generally be lower than the short run total cost, because the amount of capital can be chosen to be optimal for the amount of output.

Other economic models use the total variable cost curve (and therefore total cost curve) to illustrate the concepts of increasing, and later diminishing, marginal return.

In marketing, it is necessary to know how total costs divide between variable and fixed. "This distinction is crucial in forecasting the earnings generated by various changes in unit sales and thus the financial impact of proposed marketing campaigns." In a survey of nearly 200 senior marketing managers, 60% responded that they found the "variable and fixed costs" metric very useful.[1]

Calculating cost functions

  • Total product (= Output, Q) = Quantity of goods
  • Average Variable Cost (AVC) = Total Variable Cost / Quantity of goods (This formula is cyclic with the TVC one)
  • Average Fixed Cost (AFC) = ATC – AVC
  • Total Cost = (AVC + AFC) X Quantity of goods
  • Total Variable Cost = Variable cost per unit X Quantity of goods
  • Total Fixed Cost = TC – TVC
  • Marginal Cost = Change in Total Costs / Change in Quantity of goods
  • Marginal Product = Change in Quantity of goods / Change in Variable Factor
  • Marginal Revenue = Change in Total Revenue / Change in Quantity of goods
  • Average Product = Quantity of goods / Variable Factor
  • Total Revenue = Price X Quantity of goods
  • Average Revenue = TR / Quantity of goods
  • Total Product = AP X Variable Factor
  • Profit = TR – TC or (P-ATC)*Q
  • Loss = TC – TR (if positive)
  • Break Even Point: value of Quantity of goods where Average Revenue = Average Total Cost
  • Profit Maximizing Condition: Marginal Revenue = Marginal Cost
  • Marginal Revenue =The rate of change in Total Revenue with Quantity

See also

References

  1. ↑ Farris, Paul W.; Neil T. Bendle; Phillip E. Pfeifer; David J. Reibstein (2010). Marketing Metrics: The Definitive Guide to Measuring Marketing Performance. Upper Saddle River, New Jersey: Pearson Education, Inc. ISBN 0-13-705829-2. The Marketing Accountability Standards Board (MASB) endorses the definitions, purposes, and constructs of classes of measures that appear in Marketing Metrics as part of its ongoing Common Language in Marketing Project.

2. Fuss, M. A. (1987, January 1). Production and Cost Functions. https://link.springer.com/referenceworkentry/10.1057/978-1-349-95121-5_1668-1.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.