In geometry, the positive and negative Voronoi poles of a cell in a Voronoi diagram are certain vertices of the diagram.

Definition

Example
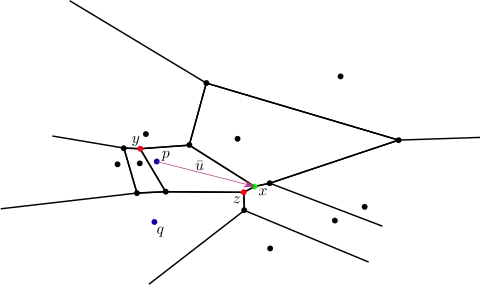
Here x is the positive pole of V_p and y its negative. As the cell corresponding to q is unbounded, only the negative pole z exists.

Let ${\displaystyle V}$ be the Voronoi diagram for a set of sites ${\displaystyle P}$, and let ${\displaystyle V_{p}}$ be the Voronoi cell of ${\displaystyle V}$ corresponding to a site ${\displaystyle p\in P}$. If ${\displaystyle V_{p}}$ is bounded, then its positive pole is the vertex of the boundary of ${\displaystyle V_{p}}$ that has maximal distance to the point ${\displaystyle p}$. If the cell is unbounded, then a positive pole is not defined.

Furthermore, let ${\displaystyle {\bar {u}}}$ be the vector from ${\displaystyle p}$ to the positive pole, or, if the cell is unbounded, let ${\displaystyle {\bar {u}}}$ be a vector in the average direction of all unbounded Voronoi edges of the cell. The negative pole is then the Voronoi vertex ${\displaystyle v}$ in ${\displaystyle V_{p}}$ with the largest distance to ${\displaystyle p}$ such that the vector ${\displaystyle {\bar {u}}}$ and the vector from ${\displaystyle p}$ to ${\displaystyle v}$ make an angle larger than ${\displaystyle {\tfrac {\pi }{2}}}$.

References

• Boissonnat, Jean-Daniel (2007). Effective Computational Geometry for Curves and Surfaces. Berlin: Springer. ISBN 978-3-540-33258-9.