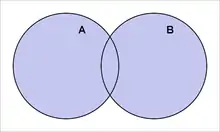
并集

在集合论和数学的其他分支中，一群集合的并集[1]，是以这群集合的所有元素來构成的集合。

A和B的并集

有限聯集

聯集是由公理化集合论的分類公理來確保其唯一存在的特定集合 $A\cup B$ ：

(\forall A)(\forall B)(\forall x)\left\{(x\in A\cup B)\Leftrightarrow \left[(x\in A)\vee (x\in B)\right]\right\}

也就是直觀上：

「對所有

x

，

x\in A\cup B

等價於

x\in A

或

x\in B

」

举例：

集合 $\{1,2,3\}$ 和 $\{2,3,4\}$ 的并集是 $\{1,2,3,4\}$ 。数 $9$ 不属于素数集合 $\{2,3,5,7,11,\ldots \}$ 和偶数集合 $\{2,4,6,8,10,\ldots \}$ 的并集，因为 $9$ 既不是素数，也不是偶数。

更通常的，多个集合的并集可以这样定义：例如， $A,B$ 和 $C$ 的并集含有所有 $A$ 的元素，所有 $B$ 的元素和所有 $C$ 的元素，而没有其他元素。形式上：

x

是

A\cup B\cup C

的元素，当且仅当

x

属于

A

或

x

属于

B

或

x

属于

C

。

代数性质

二元并集（两个集合的并集）是一种结合运算，即

A\cup (B\cup C)=(A\cup B)\cup C

。事实上，

A\cup B\cup C

也等于这两个集合，因此圆括号在仅进行并集运算的时候可以省略。

相似的，并集运算满足交换律，即集合的顺序任意。

空集是并集运算的单位元。即 $\varnothing \cup A=A$ ，对任意集合 $A$ 。可以将空集当作零个集合的并集。

结合交集和补集运算，并集运算使任意幂集成为布尔代数。例如，并集和交集相互满足分配律，而且这三种运算满足德·摩根律。若将并集运算换成对称差运算，可以获得相应的布尔环。

无限并集

由公理化集合论的并集公理，有唯一的集合 $\bigcup {\mathcal {M}}$ 滿足：

(\forall {\mathcal {M}})(\forall x)\left\{\left(x\in \bigcup {\mathcal {M}}\right)\Leftrightarrow (\exists A)\left[\left(A\in {\mathcal {M}}\right)\wedge (x\in A)\right]\right\}

也就是直觀上「對所有 ${\mathcal {M}}$ 和所有 $x$ ， $x\in \bigcup {\mathcal {M}}$ 等價於有某個 ${\mathcal {M}}$ 的下屬集合 $A$ ，使得 $x\in A$ 」。以上的 ${\mathcal {M}}$ 可以直觀的視為一個集合族，而把 $\bigcup {\mathcal {M}}$ 看成對 ${\mathcal {M}}$ 內的集合取并集，但這個公理並沒有對 ${\mathcal {M}}$ 下屬集合的數量做出任何限制，所以這個 $\bigcup {\mathcal {M}}$ 被俗稱為任意并集或无限并集。

若 $X\subseteq \bigcup {\mathcal {M}}$ ，會稱 $X$ 被 ${\mathcal {M}}$ 覆蓋（cover），也就是直觀上可以用 ${\mathcal {M}}$ 裡的所有集合疊起來蓋住 $X$ 。

例如：

對 ${\mathcal {M}}=\{A,B,C\}$ ， $\bigcup {\mathcal {M}}=A\cup B\cup C$ ，若 $M$ 是空集， $\bigcup {\mathcal {M}}$ 也是空集。

无限并集有多种表示方法：

可模仿求和符号記為

\bigcup _{A\in {\mathcal {M}}}A

。

但大多數人會假設指标集 $I$ 的存在，換句話說

若

I\,{\overset {A}{\cong }}\,{\mathcal {M}}

則

\bigcup _{i\in I}A(i):=\bigcup {\mathcal {M}}

在指标集 $I$ 是自然数系 $\mathbb {N}$ 的情况下，更可以仿无穷级数來表示，也就是說：

若

\mathbb {N} \,{\overset {A}{\cong }}\,{\mathcal {M}}

則

\bigcup _{i=0}^{\infty }A(i):=\bigcup {\mathcal {M}}

也可以更粗略直觀的將 $\bigcup _{i=0}^{\infty }A(i)$ 写作 $A_{0}\cup A_{1}\cup A_{2}\cup \ldots$ 。

无限并集的性質

定理(0) —
$\vdash \bigcup \varnothing =\varnothing$

證明
(1) $(\forall x)[\neg (x\in \varnothing )]$ (空集公理) (2) $\neg (S\in \varnothing )$ (MP with A4, 1) (3) $(S\in \varnothing )\Rightarrow [\neg (x\in S)]$ (M0 with 2) (4) $\neg \neg (S\in \varnothing )\Rightarrow [\neg (x\in S)]$ (Equv with DN, 3) (5) $\neg \{[\neg (S\in \varnothing )]\wedge [\neg (x\in S)]\}$ (Equv with De Morgan, 4) (6) $(\forall S){\big \{}\neg \{[\neg (S\in \varnothing )]\wedge [\neg (x\in S)]\}{\big \}}$ (GEN with $S$ , 5) (7) $\neg (\exists S)\{[\neg (S\in \varnothing )]\wedge [\neg (x\in S)]\}$ (Equv with DN, 6) (8) $(\forall x)\left\{\left(x\in \bigcup \varnothing \right)\Leftrightarrow (\exists S)\{(S\in \varnothing )\wedge (x\in S)\}\right\}$ (MP with 并集公理, A4) (9) $\left(x\in \bigcup \varnothing \right)\Leftrightarrow (\exists S)\{(S\in \varnothing )\wedge (x\in S)\}$ (MP with A4, 8) (10) $\left(x\in \bigcup \varnothing \right)\Rightarrow (\exists S)\{(S\in \varnothing )\wedge (x\in S)\}$ (MP with AND ,9) (11) $\neg (\exists S)\{(S\in \varnothing )\wedge (x\in S)\}\Rightarrow \neg \left(x\in \bigcup \varnothing \right)$ (MP with T, 10) (12) $\neg \left(x\in \bigcup \varnothing \right)$ (MP with 7, 11) (13) $(\forall x)\left(x\not \in \bigcup \varnothing \right)$ (GEN with $x$ , 12) (14) $(y=\varnothing )\Leftrightarrow (\forall x)[\neg (x\in y)]$ (E) (15) $(\forall y)\{(y=\varnothing )\Leftrightarrow (\forall x)[\neg (x\in y)]\}$ (GEN with $y$ , 14) (16) $\left(\bigcup \varnothing =\varnothing \right)\Leftrightarrow (\forall x)\left[\neg \left(x\in \bigcup \varnothing \right)\right]$ (MP with A4, 15) (17) $\bigcup \varnothing =\varnothing$ (Equv with 13, 16)

比較性質

定理(1) —
$({\mathcal {M}}\subseteq {\mathcal {N}})\vdash \left(\bigcup {\mathcal {M}}\subseteq \bigcup {\mathcal {N}}\right)$

證明
注意到可以從(AND)得到 $({\mathcal {P}}\Rightarrow {\mathcal {Q}}),\,({\mathcal {P}}\Rightarrow {\mathcal {R}}),\,{\mathcal {P}}\vdash {\mathcal {Q}}\wedge {\mathcal {R}}$ 換句話說，從演繹元定理有 (u) $({\mathcal {P}}\Rightarrow {\mathcal {Q}}),\,({\mathcal {P}}\Rightarrow {\mathcal {R}})\vdash {\mathcal {P}}\Rightarrow ({\mathcal {Q}}\wedge {\mathcal {R}})$ (1) $(\forall A)\left[(A\in {\mathcal {M}})\Rightarrow (A\in {\mathcal {N}})\right]$ (Hyp) (2) $(A\in {\mathcal {M}})\Rightarrow (A\in {\mathcal {N}})$ (MP with 1, A4) (3) $[(a\in A)\wedge (A\in {\mathcal {M}})]\Rightarrow (A\in {\mathcal {M}})$ (AND) (4) $[(a\in A)\wedge (A\in {\mathcal {M}})]\Rightarrow (a\in A)$ (AND) (5) $[(a\in A)\wedge (A\in {\mathcal {M}})]\Rightarrow (A\in {\mathcal {N}})$ (D1 with 2, 3) (6) $[(a\in A)\wedge (A\in {\mathcal {M}})]\Rightarrow [(a\in A)\wedge (A\in {\mathcal {N}})]$ (u with 4, 5) (7) $(\exists A\in {\mathcal {M}})(a\in A)\Rightarrow (\exists A\in {\mathcal {N}})(a\in A)$ (GENe with $A$ , 6) (8) $(\forall x)\left\{\left(x\in \bigcup {\mathcal {M}}\right)\Leftrightarrow (\exists A\in {\mathcal {M}})(x\in A)\right\}$ (MP with 并集公理, A4) (9) $(\forall x)\left\{\left(x\in \bigcup {\mathcal {N}}\right)\Leftrightarrow (\exists A\in {\mathcal {N}})(x\in A)\right\}$ (MP with 并集公理, A4) (10) $\left(x\in \bigcup {\mathcal {M}}\right)\Leftrightarrow (\exists A\in {\mathcal {M}})(x\in A)$ (MP with 8, A4) (11) $\left(x\in \bigcup {\mathcal {N}}\right)\Leftrightarrow (\exists A\in {\mathcal {N}})(x\in A)$ (MP with 9, A4) (12) $\left(x\in \bigcup {\mathcal {M}}\right)\Rightarrow (\exists A\in {\mathcal {N}})(x\in A)$ (D1 with 7, 10) (13) $\left(x\in \bigcup {\mathcal {M}}\right)\Rightarrow \left(x\in \bigcup {\mathcal {N}}\right)$ (D1 with 11, 12) (14) $(\forall x)\left[\left(x\in \bigcup {\mathcal {M}}\right)\Rightarrow \left(x\in \bigcup {\mathcal {N}}\right)\right]$ (GEN with $a$ , 13)

覆蓋性質

定理(2) —
$\vdash A=\bigcup {\mathcal {P}}(A)$

「 $A$ 正好就是其冪集的聯集」，這個定理直觀上可理解成，因為冪集 ${\mathcal {P}}(A)$ 是以 $A$ 和 $A$ 的子集為元素，所以 ${\mathcal {P}}(A)$ 的聯集理當是 $A$ 。

證明
注意到可以從(AND)得到 $({\mathcal {P}}\Rightarrow {\mathcal {Q}}),\,({\mathcal {P}}\Rightarrow {\mathcal {R}}),\,{\mathcal {P}}\vdash {\mathcal {Q}}\wedge {\mathcal {R}}$ 換句話說，從演繹元定理有 (u) $({\mathcal {P}}\Rightarrow {\mathcal {Q}}),\,({\mathcal {P}}\Rightarrow {\mathcal {R}})\vdash {\mathcal {P}}\Rightarrow ({\mathcal {Q}}\wedge {\mathcal {R}})$ (1) $(\forall x)\left\{\left[x\in \bigcup {\mathcal {P}}(A)\right]\Leftrightarrow (\exists S)\{[S\in {\mathcal {P}}(A)]\wedge (x\in S)\}\right\}$ (MP with 并集公理, A4) (2) $(\forall S)\{[S\in {\mathcal {P}}(A)]\Leftrightarrow (S\subseteq A)\}$ (幂集公理) (3) $[S\in {\mathcal {P}}(A)]\Leftrightarrow (S\subseteq A)$ (MP with A4 ,2) (4) $(\forall x)\left\{\left[x\in \bigcup {\mathcal {P}}(A)\right]\Leftrightarrow (\exists S)[(S\subseteq A)\wedge (x\in S)]\right\}$ (Equv with 1, 3) (5) $[(S\subseteq A)\wedge (x\in S)]\Rightarrow (S\subseteq A)$ (AND) (6) $(\forall x)[(x\in S)\Rightarrow (x\in A)]\Rightarrow [(x\in S)\Rightarrow (x\in A)]$ (A4) (7) $[(S\subseteq A)\wedge (x\in S)]\Rightarrow [(x\in S)\Rightarrow (x\in A)]$ (D1 with 5, 6) (8) $[(S\subseteq A)\wedge (x\in S)]\Rightarrow (x\in S)$ (AND) (9) $[(S\subseteq A)\wedge (x\in S)]\Rightarrow \{(x\in S)\wedge [(x\in S)\Rightarrow (x\in A)]\}$ (u with 7, 8) 注意到 $(x\in S),\,[(x\in S)\Rightarrow (x\in A)]\vdash (x\in A)$ 再對上式套用(AND)就有 $\{(x\in S)\wedge [(x\in S)\Rightarrow (x\in A)]\}\vdash (x\in A)$ (a) (10') $[(S\subseteq A)\wedge (x\in S)]\Rightarrow (x\in A)$ (D1 with a, 9) (11') $(\exists S)[(S\subseteq A)\wedge (x\in S)]\Rightarrow (x\in A)$ (GENe with $S$ , 10') (12') $(\forall S)\{\neg [(S\subseteq A)\wedge (x\in S)]\}\Rightarrow \{\neg [(A\subseteq A)\wedge (x\in A)]\}$ (A4) (13') $[(A\subseteq A)\wedge (x\in A)]\Rightarrow (\exists S)[(S\subseteq A)\wedge (x\in S)]$ (MP with T, 12') (14') $(x\in A)\Rightarrow (x\in A)$ (I) (15') $A\subseteq A$ (GEN with $x$ , 14') 注意到(AND)依據演繹定理可改寫為 $(A\subseteq A)\vdash (x\in A)\Rightarrow [(A\subseteq A)\wedge (x\in A)]$ (b) (16'') $(x\in A)\Rightarrow [(A\subseteq A)\wedge (x\in A)]$ (b with 15') (17'') $(x\in A)\Rightarrow (\exists S)[(S\subseteq A)\wedge (x\in S)]$ (D1 with 13', 16'') (18'') $(x\in A)\Leftrightarrow (\exists S)[(S\subseteq A)\wedge (x\in S)]$ (AND with 11', 17'') (19'') $(\forall x)\left\{\left[x\in \bigcup {\mathcal {P}}(A)\right]\Leftrightarrow (x\in A)\right\}$ (Equv with 4, 18''')

定理(3) —
$\left(\bigcup {\mathcal {M}}\subseteq A\right)\vdash (\forall M\in {\mathcal {M}})(M\subseteq A)$

直觀上，這個定理說「一群集合的聯集包含於 $A$ ，則它們個個都包含於 $A$ 」

證明
(1) $(\forall a)\left[(\exists M\in {\mathcal {M}})(a\in M)\Rightarrow (a\in A)\right]$ (Hyp) (2) $[(M\in {\mathcal {M}})\wedge (a\in M)]\Rightarrow (\exists M\in {\mathcal {M}})(a\in M)$ (A4 and T) (3) $(\exists M\in {\mathcal {M}})(a\in M)\Rightarrow (a\in A)$ (MP with 1, A4) (4) $[(M\in {\mathcal {M}})\wedge (a\in M)]\Rightarrow (a\in A)$ (D1 with 2, 3) (5) $(M\in {\mathcal {M}})\Rightarrow [(a\in M)\Rightarrow (a\in A)]$ (MP with abb, 4) (6) $(\forall a)\{(M\in {\mathcal {M}})\Rightarrow [(a\in M)\Rightarrow (a\in A)]\}$ (GEN with $a$ , 5) (7) $(M\in {\mathcal {M}})\Rightarrow (\forall a)[(a\in M)\Rightarrow (a\in A)]$ (MP with A5 , 6) (8) $(\forall M)\{(M\in {\mathcal {M}})\Rightarrow (\forall a)[(a\in M)\Rightarrow (a\in A)]\}$ (GEN with $M$ , 7)

定理(4) —
$\vdash \left(A=\bigcup {\mathcal {M}}\right)\Rightarrow \left\{A\subseteq \bigcup {\mathcal {[}}{\mathcal {M}}\cup {\mathcal {P}}(A)]\right\}$

直觀上，這個定理說「集族 ${\mathcal {M}}$ 的聯集為 $A$ ，則對 $A$ 的每點 $a$ ，都可從 ${\mathcal {M}}$ 裡找到一個 $a$ 的鄰域 $M$ ，且這個鄰域不會比 $A$ 大」

證明
注意到可以從(AND)得到 $({\mathcal {P}}\Rightarrow {\mathcal {Q}}),\,({\mathcal {P}}\Rightarrow {\mathcal {R}}),\,{\mathcal {P}}\vdash {\mathcal {Q}}\wedge {\mathcal {R}}$ 換句話說，從演繹元定理有 (u) $({\mathcal {P}}\Rightarrow {\mathcal {Q}}),\,({\mathcal {P}}\Rightarrow {\mathcal {R}})\vdash {\mathcal {P}}\Rightarrow ({\mathcal {Q}}\wedge {\mathcal {R}})$ (1) $(\forall a)\left[(a\in A)\Leftrightarrow (\exists M\in {\mathcal {M}})(a\in M)\right]$ (Hyp) (2) $(\forall M\in {\mathcal {M}})(M\subseteq A)$ (MP with 1, 定理3) (3) $(M\in {\mathcal {M}})\Rightarrow (M\subseteq A)$ (MP with A4, 2) (4) $[(a\in M)\wedge (M\in {\mathcal {M}})]\Rightarrow (M\in {\mathcal {M}})$ (AND) (5) $[(a\in M)\wedge (M\in {\mathcal {M}})]\Rightarrow (a\in M)$ (AND) (6) $[(a\in M)\wedge (M\in {\mathcal {M}})]\Rightarrow (M\in {\mathcal {M}})$ (AND) (7) $[(a\in M)\wedge (M\in {\mathcal {M}})]\Rightarrow (M\subseteq A)$ (D1 with 3, 4) (8) $[(a\in M)\wedge (M\in {\mathcal {M}})]\Rightarrow [(a\in M)\wedge (M\in {\mathcal {M}})]$ (a with 5, 6) (9) $[(a\in M)\wedge (M\in {\mathcal {M}})]\Rightarrow [(a\in M)\wedge (M\in {\mathcal {M}})\wedge (M\subseteq A)]$ (a with 7, 8) (10) $(\exists M\in {\mathcal {M}})(a\in M)\Rightarrow (\exists M\in {\mathcal {M}})[(a\in M)\wedge (M\subseteq A)]$ (GENe with $M$ , 9) (11) $(a\in A)\Leftrightarrow (\exists M\in {\mathcal {M}})(a\in M)$ (MP with A4, 1) (12) $(a\in A)\Rightarrow (\exists M\in {\mathcal {M}})(a\in M)$ (AND with 11) (13) $(a\in A)\Rightarrow (\exists M\in {\mathcal {M}})[(a\in M)\wedge (M\subseteq A)]$ (D1 with 10, 12) (14) $(\forall a\in A)(\exists M\in {\mathcal {M}})[(a\in M)\wedge (M\subseteq A)]$ (GEN with $a$ , 13) (15) $(\forall S)\{[S\in {\mathcal {P}}(A)]\Leftrightarrow (S\subseteq A)\}$ (幂集公理) (16) $[M\in {\mathcal {P}}(A)]\Leftrightarrow (M\subseteq A)$ (MP with A4, 15) (17) $(\forall a\in A)(\exists M\in {\mathcal {M}})\{(a\in M)\wedge [M\in {\mathcal {P}}(A)]\}$ (Equv with 14, 16) (18) $(\forall A)(\forall B)(\forall x)\left\{(x\in A\cap B)\Leftrightarrow \left[(x\in A)\wedge (x\in B)\right]\right\}$ (有限交集) (19) $(\forall B)(\forall x)\left\{(x\in {\mathcal {M}}\cap B)\Leftrightarrow \left[(x\in {\mathcal {M}})\wedge (x\in B)\right]\right\}$ (MP with A4, 18) (20) $(\forall x){\big \{}[x\in {\mathcal {M}}\cap {\mathcal {P}}(A)]\Leftrightarrow \left\{(x\in {\mathcal {M}})\wedge [x\in {\mathcal {P}}(A)]\right\}{\big \}}$ (MP with A4, 19) (21) $[M\in {\mathcal {M}}\cap {\mathcal {P}}(A)]\Leftrightarrow \left\{(M\in {\mathcal {M}})\wedge [M\in {\mathcal {P}}(A)]\right\}$ (MP with A4, 20) (22) $(\forall a\in A)(\exists M)\{(a\in M)\wedge [M\in {\mathcal {M}}\cap {\mathcal {P}}(A)]\}$ (Equv with 17, 21) (23) $\left\{a\in \bigcup [{\mathcal {M}}\cap {\mathcal {P}}(A)]\right\}\Leftrightarrow (\exists M)\{(a\in M)\wedge [M\in {\mathcal {M}}\cap {\mathcal {P}}(A)]\}$ (MP with 并集公理, A4) (24) $(\forall a)\left\{(a\in A)\Rightarrow \left\{a\in \bigcup [{\mathcal {M}}\cap {\mathcal {P}}(A)]\right\}\right\}$ (Equv with 22, 23)

運算性質

定理(5) —
若

{\mathcal {M}}_{A}:=\left\{B\,|\,(\exists M\in {\mathcal {M}})(B=M\cap A)\right\}

則

\vdash \bigcup {\mathcal {M}}_{A}=A\cap \left(\bigcup {\mathcal {M}}\right)

證明
(1) $(\forall B)[(B\in {\mathcal {M}}_{A})\Leftrightarrow (\exists M\in {\mathcal {M}})(B=M\cap A)]$ ( ${\mathcal {M}}_{A}$ 的定義) (2) $(\forall x)\left\{\left(x\in \bigcup {\mathcal {M}}\right)\Leftrightarrow (\exists B\in {\mathcal {M}})(x\in B)\right\}$ (MP with 并集公理, A4) (3) $(\forall A)(\forall B)(\forall x)\left\{(x\in A\cap B)\Leftrightarrow \left[(x\in A)\wedge (x\in B)\right]\right\}$ (有限交集) (4) $\left(x\in \bigcup {\mathcal {M}}_{A}\right)\Leftrightarrow (\exists B)[(B\in {\mathcal {M}}_{A})\wedge (x\in B)]$ (MP with A4, 2) (5) $(B\in {\mathcal {M}}_{A})\Leftrightarrow (\exists M\in {\mathcal {M}})(B=M\cap A)$ (MP with A4, 1) (6) $\left(x\in \bigcup {\mathcal {M}}_{A}\right)\Leftrightarrow (\exists B)[(x\in B)\wedge (\exists M\in {\mathcal {M}})(B=M\cap A)]$ (Equv with 4, 5) (7) $\left(x\in \bigcup {\mathcal {M}}_{A}\right)\Leftrightarrow (\exists B)(\exists M)[(x\in B)\wedge (M\in {\mathcal {M}})\wedge (B=M\cap A)]$ (Equv with Ce, 6) (8) $\left(x\in \bigcup {\mathcal {M}}_{A}\right)\Leftrightarrow (\exists M)(\exists B)[(x\in B)\wedge (M\in {\mathcal {M}})\wedge (B=M\cap A)]$ (Equv with 量詞可交換性 ,7) (9) $(B=M\cap A)\Rightarrow \{[(x\in B)\wedge (M\in {\mathcal {M}})\wedge (B=M\cap A)]\Rightarrow [(x\in M\cap A)\wedge (M\in {\mathcal {M}})\wedge (M\cap A=M\cap A)]\}$ (E2) (10) $[(x\in B)\wedge (M\in {\mathcal {M}})\wedge (B=M\cap A)]\Rightarrow (B=M\cap A)$ (AND) (11) $[(x\in B)\wedge (M\in {\mathcal {M}})\wedge (B=M\cap A)]$ $\Rightarrow \{[(x\in B)\wedge (M\in {\mathcal {M}})\wedge (B=M\cap A)]\Rightarrow [(x\in M\cap A)\wedge (M\in {\mathcal {M}})\wedge (M\cap A=M\cap A)]\}$ (D1 with 9,10) (12) $\{[(x\in B)\wedge (M\in {\mathcal {M}})\wedge (B=M\cap A)]\Rightarrow [(x\in B)\wedge (M\in {\mathcal {M}})\wedge (B=M\cap A)]\}$ $\Rightarrow \{[(x\in B)\wedge (M\in {\mathcal {M}})\wedge (B=M\cap A)]\Rightarrow [(x\in M\cap A)\wedge (M\in {\mathcal {M}})\wedge (M\cap A=M\cap A)]\}$ (MP with A2, 11) (13) $[(x\in B)\wedge (M\in {\mathcal {M}})\wedge (B=M\cap A)]\Rightarrow [(x\in B)\wedge (M\in {\mathcal {M}})\wedge (B=M\cap A)]$ (I) (14) $[(x\in B)\wedge (M\in {\mathcal {M}})\wedge (B=M\cap A)]\Rightarrow [(x\in M\cap A)\wedge (M\in {\mathcal {M}})\wedge (M\cap A=M\cap A)]$ (MP with 12, 13) (15) $[(x\in M\cap A)\wedge (M\in {\mathcal {M}})\wedge (M\cap A=M\cap A)]\Rightarrow [(x\in M\cap A)\wedge (M\in {\mathcal {M}})]$ (AND) (16) $[(x\in B)\wedge (M\in {\mathcal {M}})\wedge (B=M\cap A)]\Rightarrow [(x\in M\cap A)\wedge (M\in {\mathcal {M}})]$ (D1 with 14,15) (17) $(\exists M)(\exists B)[(x\in B)\wedge (M\in {\mathcal {M}})\wedge (B=M\cap A)]\Rightarrow (\exists M)[(x\in M\cap A)\wedge (M\in {\mathcal {M}})]$ (GENe with $B$ then $M$ ) (18) $M\cap A=M\cap A$ (E1) 注意到配合(AND)和演繹定理有 ${\mathcal {P}}\vdash {\mathcal {R}}\Rightarrow ({\mathcal {R}}\wedge {\mathcal {P}})$ (a) (19) $[(x\in M\cap A)\wedge (M\in {\mathcal {M}})]\Rightarrow [(x\in M\cap A)\wedge (M\in {\mathcal {M}})\wedge (M\cap A=M\cap A)]$ (a with 18) (20) $(\forall B)\{\neg [(x\in B)\wedge (M\in {\mathcal {M}})\wedge (B=M\cap A)]\}\Rightarrow \{\neg [(x\in M\cap A)\wedge (M\in {\mathcal {M}})\wedge (M\cap A=M\cap A)]\}$ (A4) (21) $[(x\in M\cap A)\wedge (M\in {\mathcal {M}})\wedge (M\cap A=M\cap A)]\Rightarrow (\exists B)[(x\in B)\wedge (M\in {\mathcal {M}})\wedge (B=M\cap A)]$ (MP with T, 20) (22) $[(x\in M\cap A)\wedge (M\in {\mathcal {M}})]\Rightarrow (\exists B)[(x\in B)\wedge (M\in {\mathcal {M}})\wedge (B=M\cap A)]$ (D1 with 19, 21) (23) $(\exists M)[(x\in M\cap A)\wedge (M\in {\mathcal {M}})]\Rightarrow (\exists M)(\exists B)[(x\in B)\wedge (M\in {\mathcal {M}})\wedge (B=M\cap A)]$ (GENe with $M$ ) (24) $(\exists M)(\exists B)[(x\in B)\wedge (M\in {\mathcal {M}})\wedge (B=M\cap A)]\Leftrightarrow (\exists M)[(x\in M\cap A)\wedge (M\in {\mathcal {M}})]$ (AND with 17, 23) (25) $\left(x\in \bigcup {\mathcal {M}}_{A}\right)\Leftrightarrow (\exists M)[(x\in M\cap A)\wedge (M\in {\mathcal {M}})]$ (Equv with 8, 24) (26) $(x\in M\cap A)\Leftrightarrow [(x\in M)\wedge (x\in A)]$ (MP with A4, 3) (27) $\left(x\in \bigcup {\mathcal {M}}_{A}\right)\Leftrightarrow (\exists M)[(x\in M)\wedge (x\in A)\wedge (M\in {\mathcal {M}})]$ (Equv with 25, 26) (28) $\left(x\in \bigcup {\mathcal {M}}_{A}\right)\Leftrightarrow \{(\exists M)[(x\in M)\wedge (M\in {\mathcal {M}})]\wedge (x\in A)\}$ (Equv with Ce, 27) (30) $\left(x\in \bigcup {\mathcal {M}}\right)\Leftrightarrow (\exists M\in {\mathcal {M}})(x\in M)$ (MP with A4, 2) (31) $\left(x\in \bigcup {\mathcal {M}}_{A}\right)\Leftrightarrow \left[\left(x\in \bigcup {\mathcal {M}}\right)\wedge (x\in A)\right]$ (Equv with 28, 30) (32) $\left[x\in A\cap \left(\bigcup {\mathcal {M}}\right)\right]\Leftrightarrow \left[(x\in A)\wedge \left(x\in \bigcup {\mathcal {M}}\right)\right]$ (MP with A4, 3) (33) $\left[x\in A\cap \left(\bigcup {\mathcal {M}}\right)\right]\Leftrightarrow \left(x\in \bigcup {\mathcal {M}}_{A}\right)$ (Equv with 31, 32) (34) $(\forall x)\left\{\left[x\in A\cap \left(\bigcup {\mathcal {M}}\right)\right]\Leftrightarrow \left(x\in \bigcup {\mathcal {M}}_{A}\right)\right\}$ (GEN with $x$ , 33)

直觀上這個定理說，交集在「无限并集满足分配律」，一般會不正式的寫為

\bigcup _{i\in I}\left(A\cap B_{i}\right)=A\cap \bigcup _{i\in I}B_{i}

定理(6) —
$\mathbb {N} \,{\overset {A}{\cong }}\,{\mathcal {A}}$ ，若對自然数 $m\in \mathbb {N}$ 做以下的符號定義：

{\mathcal {A}}_{m}:=\left\{S\in {\mathcal {A}}\,|\,A^{-1}(S)\geq m\right\}

{\mathcal {I}}:=\left\{S\,{\bigg |}\,(\exists m\in \mathbb {N} )\left(S=\bigcap {\mathcal {A}}_{m}\right)\right\}

{\mathcal {S}}:=\left\{S\,{\bigg |}\,(\exists m\in \mathbb {N} )\left(S=\bigcup {\mathcal {A}}_{m}\right)\right\}

那有

\vdash \bigcup {\mathcal {I}}\subseteq \bigcap {\mathcal {S}}

。

這個定理一般會被不正式的寫為

\bigcup _{i=0}^{\infty }\left(\bigcap _{j=i}^{\infty }A_{j}\right)\subseteq \bigcap _{i=0}^{\infty }\left(\bigcup _{j=i}^{\infty }A_{j}\right)

。

参考

参考文献

程极泰. . 应用数学丛书第一版. 国防工业出版社. 1985: 14. 15034.2766.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] 程极泰. . 应用数学丛书第一版. 国防工业出版社. 1985: 14. 15034.2766.