一进制
一進位系統是一個雙射,以1為底数的記數系統。這是一個代表自然數最簡單的記數系統:要表示一個自然數N,我們任意的先選用一個符號代表“一”,然後將之重複N次。舉例來說,使用|(一個計數符號)作為符號,數字六則以||||||表示。若符號選用1,則數字1、 2、 3、 4、 5、 6在一进制中表示為1、 11、 111、 1111、 11111、 111111 …(OEIS數列A000042)[1]。用手指計算的方法也是一種一進位系統。一進位系統對進行中結果的計數或者計算很有用,像是 體育比賽內的分數,因為一進位系統沒有中介的結果需要被刪去或者捨棄。
| 记数系统 | |
|---|---|
| 印度-阿拉伯数字系统 | |
| 西方阿拉伯数字 阿拉伯文数字 高棉數字 孟加拉数字 |
印度數字 波羅米數字 泰语数字 |
| 漢字文化圈記數系統 | |
| 中文数字 閩南語數字 越南语数字 算筹 |
日語數字 數字 苏州码子 |
| 字母記數系統 | |
| 阿拉伯字母數字 亚美尼亚数字 西里爾數字 吉茲數字 |
希伯來數字 希腊数字 阿利耶波多數字 |
| 其它記數系統 | |
| 阿提卡數字 巴比倫數字 古埃及数字 伊特拉斯坎數字 |
玛雅数字 罗马数字 熙笃会数字 卡克托维克数字 |
| 依底数区分的进位制系统 | |
| 1 2 3 4 5 6 8 9 10 11 12 16 20 36 60 | |
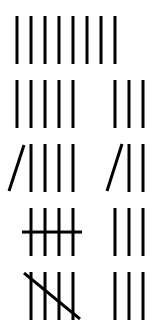

為了易讀性,一進位的符號常常以五個為一組湊在一起。這有點類似十進位系統裡面,實際使用上常常會以空白或者逗號分隔數字,讓100,000,000這種大數字比較易讀。第一或者第五個符號可能會彎一個角度作為區別。其他一進位系統以五湊成一堆的例子則是漢字文化圈傳統使用的正字標記,這個字有五個筆劃,有東西新增時就多寫一筆。左邊圖上面的第四個範例,第五個筆劃將前面四個湊成五個一組,因為這組符號的形狀,有時這種方法被稱為“herringbone”(鯡魚骨)記數法。
在巴西以及法國,另一類系統經常被使用:作為像是鯡魚骨這樣將這些“棍棒”排成一排的替代,這個系統是將四個符號排成一個方塊,第五個符號則劃過這個方塊的對角。
加法和減法在一進位系統使用特別容易,因為僅僅牽涉比字串的串接稍多的操作。然而,乘法和除法則複雜許多。
與其他系統不同,在一進位系統裡面並沒有代表0的符號存在,因此一進位是只有一個符號的雙射系統。如果有代表「零」的符號,那這個系統就會變成二進位。實際上存在的一進位系統沒有辦法明確表示零,雖然甚麼都不寫常常被用來隱含這個含意。即使在比較先進的計數系統,像是羅馬數字裡面,也不存在代表零的符號,相對的這系統使用nullae,也就是拉丁文的“甚麼都沒有”(nothing)。
與標準的進制相比,一進位系統在大型計算很不方便,因此不在實際上使用。不過有時因此會讓這系統出現在計算理論裡面的一些決定性問題(像是一些P-完全問題)作為輸入,作為“人工的”縮減問題的計算時間或者空間。舉例,整數分解這個問題,如果輸入是以二進位給予,那一般認為的運作時間會超過輸入長度的多項式時間;但是,如果輸入是以一進位給予,則變成只需要線性的時間。不過這作法其實有些誤導:使用一進位作為輸入本來就會導致輸入這動作變慢。使用一進位與其他二進位(或者以上)的輸入模式,差異會根據輸入本身等比例差異到對數(以二為底或者以上)倍;所以運作時間與空間看起來相對於輸入長度比較好時,並非是因為我們的演算法變好,而是因為我們故意使用比較長的輸入方式。
實際使用
在古代數學裡面實際使用一進位系統的例子,可以參見莫斯科數學紙草書,其使用日期大約前18世紀左右。
一進位也在一些資料壓縮的演算法裡面使用;作為例子可參見格倫布編碼。
一種特殊的一進位系統TeX的軟體版本號上面使用,其版本號碼是一部份圆周率的十進位表示 – 版本號碼是位數的個數。現在的版本號是3.1415926,而這個數字會漸漸地接近π。
參見
- 邱奇數
- 皮亞諾公理
參考文獻
- Hext, Jan, , Programming Structures 1, Prentice Hall: 33, 1990, ISBN 9780724809400.