3氦過程

3氦過程是一組核融合反應，通過這些反應，將三個氦-4核（α粒子）轉化為碳核[1][2]。

  「」至此，您可能想尋找頁面氦核作用。
3氦過程概述
以對數呈現不同溫度（T）下質子-質子（PP）、碳氮氧 （CNO）和3氦融合過程的相對能量輸出（ε）。虛線顯示了恒星內PP和CNO過程聯合的能量生成。在太陽核心的溫度下，PP過程會更有效率。

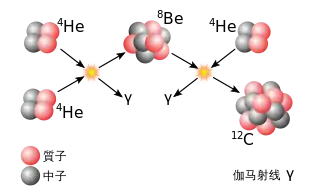
恆星中的3氦過程

氦是質子-質子鏈反應和CNO的產物，累積在恆星的核心中。

兩個氦-4核的核融合反應產生高度不穩定的鈹-8，並衰變回半衰期為8.19×10−17 s的較小核，除非在這段時間內第三個α粒子與鈹-8核融合[3]為了產生碳-12的激發共振態，[4]被稱為霍伊爾態，它幾乎總是衰變回三個α粒子，但大約2421.3次中就有一次釋放能量並變為碳-12的穩定態形式[5]。當恆星核心的氫耗盡時，它開始收縮和升溫。如果中心溫度上升到108K[6]，是太陽核心溫度的六倍，α粒子就能够以足够快的速度融合，通過鈹-8屏障，產生大量穩定的碳-12。

4
2He
 + 4
2He
 → 8
4Be
  (−0.0918 MeV)
8
4Be
 + 4
2He
 → 12
6C
 + 2
γ
 		 (+7.367 MeV)

這些過程的淨能量釋放為7.275 MeV。

作為這個過程的副作用，一些碳核與額外的氦融合，產生穩定的氧和能量同位素：

12
6C
 + 4
2He
 → 16
8O
 +
γ
 (+7.162 MeV)

氦與氫的核融合反應產生鋰-5，它也是高度不穩定的，並衰變回更小的原子核，半衰期為3.7×10−22 s。

與額外的氦核融合可以在被稱為氦核作用的恆星核合成鏈中產生更重的元素，但這些反應只有在比經歷3α過程的核心更高的溫度和壓力下才顯著。這就造成了恆星核合成產生大量碳和氧的情况，但這些元素中只有一小部分轉化為氖和更重的元素。氧氣和碳是氦-4燃燒的主要「灰燼」。

原始的碳
条目：太初核合成

由於3氦過程需要較長的時間才能形成碳，因此在太初核合成不太可能發生。此一結果可以說明大爆炸為何沒有製造出碳，因為在大爆炸之後的一分鐘，就已經低於3氦過程所需要的溫度了。

共振

通常情况下，3氦過程的概率非常小。然而，鈹-8基態的能量幾乎與兩個α粒子的能量完全相同。在第二個步驟中，8Be + 4He幾乎具有12C在激發態的完全能量。這種共振的存在是弗雷德·霍伊爾在實際觀測到之前預測的，基於它存在的物理必要性，以便在恆星中形成碳。這種能量共振和過程的預測和發現為霍伊爾的恆星核合成假說提供了非常重要的支持，該假說認為所有化學元素最初都是由氫形成的，氫是真正的原始物質。人擇原理被用來解釋這樣一個事實，即核共振被敏感地安排在宇宙中產生大量的碳和氧[7][8]。

重元素的核合成

隨著溫度和密度的進一步增加，核融合過程產生的核素僅能達到鎳-56（後來衰變為鐵）；更重的元素（比鎳更重的元素）主要由中子捕獲產生。慢中子的捕獲，即S-過程，產生了大約一半原子序大於鐵的元素。另一半可能發生在核坍縮超新星和中子星合併過程的快中子捕獲，即R-過程產生的[9]。

反應速率與恒星演化

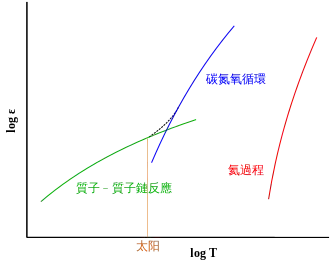
3氦過程在很大程度上取決於恆星核心物質的溫度和密度。反應釋放的功率大約與溫度的40次方與密度的平方成正比[10]。相對的，質子-質子鏈反應以與溫度的四次方成比例的速率產生能量，碳氮氧循環以大約溫度的17次方產生能量，並且兩者都與密度成線性比例。這種强烈的溫度依賴性對恆星演化的晚期，即紅巨星階段產生了影響。

對於紅巨星分支上的低質量恆星，只有通過電子簡併壓力才能防止核心中心累積的氦進一步坍縮。整個簡併核心處於相同的溫度和壓力下，因此當其密度足够高時，3氦過程的核融合會貫穿整個核心同時進行。但在壓力高到足夠解除簡併態之前，核心無法膨脹以對新增產生的能量做出反應。因此，溫度升高，導致正回饋迴圈中的反應速率增加，成為失控反應。這個過程被稱為氦閃，只持續幾秒鐘，但就能燃燒掉堆積在核芯中60-80%的氦。在核心氦閃期間，恆星產生的能量可以達到大約1011太陽光度，這與整個星系的光度相當[11]，但因為所有的能量都被用來將核心從簡併態提升到正常的氣態，因此在表面不會立即觀察到任何影響。由於核心不再是簡併態，流體靜力平衡再次建立，恆星開始在核心「燃燒」氦，並在核心外圍的球形殼層中「燃燒」氫。該恆星進入穩定的氦燃燒階段，持續時間約為其在主序星上花費時間的10%（預計太陽在氦閃後將在其核心燃燒氦約10億年）[12]。

對於質量更高的恆星，碳會聚集在核心，氦則轉移到周圍的殼層，並在那裡進行氦燃燒。在這個氦殼層中，壓力較低，質量不受電子簡併性的支持。因此，與恆星的中心相反，氦殼層能够響應殼層中增加的熱壓力而膨脹。膨脹使這一層冷卻並減緩了反應，導致恆星再次收縮。這一過程週期性地繼續，經歷這一過程的恆星將具有週期性變化的半徑和功率產生。這些恆星在膨脹和收縮時也會失去最外層的物質。

發現

3氦過程高度依賴碳-12和鈹-8的共振能量略高於氦-4。根據已知的共振，迄1952年，普通恆星似乎不可能產生碳和任何更重的元素[13]。核子物理學家威廉·福勒注意到了8Be（鈹-8）的共振，埃德溫·薩爾皮特考慮到這種共振，計算了8Be、12C和16O核合成的反應速率[14][15]。可是，薩爾皮特計算出紅巨星在2.108K或更高的溫度下燃燒氦，但最近的其它工作假設紅巨星的核心溫度低至1.1·108K。

薩爾皮特的論文順便提到了碳-12中未知的共振會對其計算產生影響，但作者從未進一步計算其影響。反而是天體物理學家佛萊德·霍伊爾，在1953年利用宇宙中存在豐富的碳-12做為存在碳-12共振的證據。霍伊爾同時發現能產生大量碳和氧的唯一方法是3氦過程通過在7.68MeV附近共振產生碳-12，這也將消除薩爾皮特計算中的差異[13]。

霍伊爾去了設在加州理工學院的福勒實驗室，說在碳-12原子核中必須有一個7.68MeV的共振（有報導稱，在大約7.5MeV時存在激發態[13]。) 。佛萊德·霍伊爾（Fred Hoyle）在這方面的大膽表現是驚人的，最初實驗室的核子物理學家對此持懷疑的態度。最後，一位剛從莱斯大學畢業的初級物理學家沃德·威林，他正在尋找一個專案提目，結果决定尋找這個共振。福勒允許他使用一台已經不再使用，老舊的范德格拉夫起電機。霍伊爾回到劍橋後，沒幾個月，福勒的實驗室在7.65MeV附近發現了碳-12的共振，證實了他的預測。核子物理學家沃德·威林在美國物理學會的夏季會議上發表的這一篇論文中，將霍伊爾列為第一作者。霍伊爾和福勒很快進行了長期而富有成效的合作，福勒甚至來到了劍橋[16]。

最終的反應結果處在+0（自旋0和正宇稱）。由於霍伊爾狀態被預測為0+或2+狀態，預期電子-正電子對或伽瑪射線將被看到。然而，在進行實驗時，沒有觀測到伽瑪射線的反應通道，這意味著狀態必須是0+。這種狀態完全抑制單獨的伽瑪輻射，因為每個伽瑪輻射必須帶走至少1角動量單位。成對產生來自激發的0+狀態是可能的，因為它們的組合自旋（0）可以耦合到一個反應，使它的角動量為0 [17]。

不可能性和微調

碳是所有已知生命的必要組成部分。12C是一種穩定的碳同位素，由於三個因素在恆星中大量產生：

  1. 一個8Be核的衰變壽命比兩個4He核（α粒子）散射的時間大四個數量級[18]。
  2. 12C原子核的激發態存在於8Be + 4He能級之上一點（0.3193 MeV）。這是必要的，因為12C的基態比8Be + 4He的能量低7.3367MeV；一個88Be核不能和一個4He核合理地直接融合成基態的12C核。然而，8Be和4He利用它們碰撞的動能融合成被激發的12C（動能提供了達到激發態所需的額外0.3193 MeV），然後其可以轉變到穩定的基態。根據一項計算，這種激發態的能級必須在大約7.3MeV和7.9MeV之間，才能產生足够的碳來維持生命，並且必須進一步「微調」到7.596 MeV和7.716 MeV之間才能產生自然界中觀察到數量豐富的12C [19]。霍伊爾態已被量測為在12C的基態之上約7.65 MeV[20]。
  3. 在12C + 4He → 16O的反應上，存在氧的激發態，如果它稍高，將提供共振並加速反應。在這種情況下，自然界中會存在碳不足的現象；幾乎所有的碳都會轉化為氧[18]。

一些學者認為，7.656 MeV的霍伊爾共振不太可能僅僅是偶然的結果。弗雷德·霍伊尔在1982年認為，霍伊爾共振是「超智者」的證據[13]；李奧納特·色斯金在《宇宙景觀》中駁斥了霍伊爾的超智者論點[21]。相反的，一些科學家認為，不同的宇宙，即龐大的「多元宇宙」的一部分，有不同的基本常數[22]：根據這個有爭議的微調假說，生命只能在少數幾個基本常數恰好經過微調以支持生命存在的宇宙中進化。由於缺乏獨立的證據，其他科學家拒絕接受多元宇宙的假設[23]。

相關條目

參考資料
  1. Appenzeller; Harwit; Kippenhahn; Strittmatter; Trimble (编). 3rd. New York: Springer. 1998.
  2. Carroll, Bradley W. & Ostlie, Dale A. . Addison Wesley, San Francisco. 2007. ISBN 978-0-8053-0348-3.
  3. Bohan, Elise; Dinwiddie, Robert; Challoner, Jack; Stuart, Colin; Harvey, Derek; Wragg-Sykes, Rebecca; Chrisp, Peter; Hubbard, Ben; Parker, Phillip. . Foreword by David Christian 1st American. New York: DK. February 2016: 58. ISBN 978-1-4654-5443-0. OCLC 940282526. 已忽略未知参数|collaboration= (帮助)
  4. Audi, G.; Kondev, F. G.; Wang, M.; Huang, W. J.; Naimi, S. (PDF). Chinese Physics C. 2017, 41 (3): 030001. Bibcode:2017ChPhC..41c0001A. doi:10.1088/1674-1137/41/3/030001.
  5. The carbon challenge （页面存档备份，存于）, Morten Hjorth-Jensen, Department of Physics and Center of Mathematics for Applications, University of Oslo, N-0316 Oslo, Norway: 9 May 2011, Physics 4, 38
  6. Wilson, Robert. . . Basingstoke: Taylor & Francis. 1997. ISBN 9780203212738.
  7. For example, John Barrow; Frank Tipler. . 1986.
  8. Fred Hoyle, "The Universe: Past and Present Reflections." Engineering and Science, November, 1981. pp. 8–12
  9. Pian, E.; d'Avanzo, P.; Benetti, S.; Branchesi, M.; Brocato, E.; Campana, S.; Cappellaro, E.; Covino, S.; d'Elia, V.; Fynbo, J. P. U.; Getman, F.; Ghirlanda, G.; Ghisellini, G.; Grado, A.; Greco, G.; Hjorth, J.; Kouveliotou, C.; Levan, A.; Limatola, L.; Malesani, D.; Mazzali, P. A.; Melandri, A.; Møller, P.; Nicastro, L.; Palazzi, E.; Piranomonte, S.; Rossi, A.; Salafia, O. S.; Selsing, J.; et al. . Nature. 2017, 551 (7678): 67–70. Bibcode:2017Natur.551...67P. PMID 29094694. S2CID 3840214. arXiv:1710.05858 可免费查阅. doi:10.1038/nature24298.
  10. Carroll, Bradley W.; Ostlie, Dale A. 2nd. Addison-Wesley, San Francisco. 2006: 312–313. ISBN 978-0-8053-0402-2.
  11. Carroll, Bradley W.; Ostlie, Dale A. 2nd. Addison-Wesley, San Francisco. 2006: 461–462. ISBN 978-0-8053-0402-2.
  12. . faculty.wcas.northwestern.edu. [2020-07-29].
  13. Kragh, Helge (2010) When is a prediction anthropic? Fred Hoyle and the 7.65 MeV carbon resonance. http://philsci-archive.pitt.edu/5332/ （页面存档备份，存于）
  14. Salpeter, E. E. . The Astrophysical Journal. 1952, 115: 326–328. Bibcode:1952ApJ...115..326S. doi:10.1086/145546.
  15. Salpeter, E. E. . Annu. Rev. Astron. Astrophys. 2002, 40: 1–25. Bibcode:2002ARA&A..40....1S. doi:10.1146/annurev.astro.40.060401.093901.
  16. Fred Hoyle, A Life in Science, Simon Mitton, Cambridge University Press, 2011, pages 205–209.
  17. Cook, CW; Fowler, W.; Lauritsen, C.; Lauritsen, T. . Physical Review. 1957, 107 (2): 508–515. Bibcode:1957PhRv..107..508C. doi:10.1103/PhysRev.107.508.
  18. Uzan, Jean-Philippe. . Reviews of Modern Physics. April 2003, 75 (2): 403–455. Bibcode:2003RvMP...75..403U. S2CID 118684485. arXiv:hep-ph/0205340 可免费查阅. doi:10.1103/RevModPhys.75.403.
  19. Livio, M.; Hollowell, D.; Weiss, A.; Truran, J. W. . Nature. 27 July 1989, 340 (6231): 281–284. Bibcode:1989Natur.340..281L. S2CID 4273737. doi:10.1038/340281a0.
  20. Freer, M.; Fynbo, H. O. U. (PDF). Progress in Particle and Nuclear Physics. 2014, 78: 1–23. Bibcode:2014PrPNP..78....1F. doi:10.1016/j.ppnp.2014.06.001. （原始内容存档 (PDF)于2022-07-18）.
  21. Peacock, John. . American Scientist. 2006, 94 (2): 168–170. JSTOR 27858743. doi:10.1511/2006.58.168.
  22. . New Scientist. 1 September 2016 [15 January 2017].
  23. Barnes, Luke A. . Publications of the Astronomical Society of Australia. 2012, 29 (4): 529–564. Bibcode:2012PASA...29..529B. arXiv:1112.4647 可免费查阅. doi:10.1071/as12015 可免费查阅.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.