倒易点阵
倒易点阵(英語:),又称倒(易)晶格、倒(易)格子,是物理学中描述空间波函数的傅立叶变换后的周期性的一种方法。相对于正晶格所描述的实空间周期性,倒晶格描述的是动量空间,亦可认为是k空间的周期性。根据位置和动量所满足的庞特里亚金对偶性,布拉菲晶格的倒晶格仍然是一种布拉菲晶格,而倒晶格的倒晶格就会变回原始晶格(正晶格)。
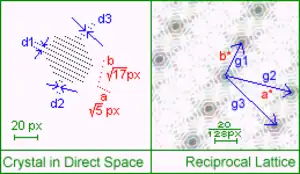
一个二维晶体及其倒易点阵
数学描述
一维晶格
对于以为基矢的一维晶格,其倒格子的基矢为
三维晶格
對三維晶格而言,我們定義素晶胞的基矢 ,可以用下列公式決定倒晶格的晶胞基矢
倒晶格的物理意义
在此以一维晶格为例。在一个以为基矢的一维晶格中,其波函数应该为布洛赫波
定义其倒晶格向量
以及一个函数
由于是一个布洛赫波包,满足
所以
也是一个布洛赫波包。则波函数有以下性质
可见,倒晶格向量G描述了波函数在以k为基矢的动量空间(k空间)内的周期性。其向量单位,即倒晶格的基矢是描述k空间中平移对称性的基矢。其最小可重复单位,即倒晶格的晶胞,称为第一布里渊区。由于波矢k和动量与波函数对应的能量密切相关,在能带理论中也用来解释能带的周期性。
倒晶格与晶体衍射
晶体衍射满足布拉格定律
定义入射波波矢为,则上述公式可变换为
因此满足布拉格定律的晶体衍射反映的不是正晶格,而是倒晶格。
进一步将以上公式转化为向量形式,定义入射波波矢为,反射波波矢为,可以得到
这个形式也和劳厄方程式相符。
晶体衍射的想法也可以用来解释能带结构中,为什么能量的分布是不連續的。
常见布拉菲晶格的倒晶格
外部連結
| 维基共享资源中相关的多媒体资源:倒易点阵 |
- (英文)http://newton.umsl.edu/run//nano/known.html (页面存档备份,存于) - Jmol-based electron diffraction simulator lets you explore the intersection between reciprocal lattice and Ewald sphere during tilt.
- (英文)DoITPoMS Teaching and Learning Package on Reciprocal Space and the Reciprocal Lattice(页面存档备份,存于)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.