側台塔截角立方體
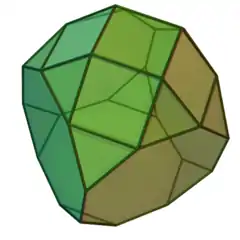
在几何学里, 侧台塔截角立方体 是约翰逊多面体之一 (J66)。 正像其名字所暗示的, 它可以通过把 正四角台塔(J4) 和 截角立方体的各自一个八边形面结合起来得到。

侧台塔截角立方体展开图
 | |
| 類別 | 约翰逊多面体 J65 - J66 - J67 |
|---|---|
| 對偶多面體 | - |
| 識別 | |
| 鮑爾斯縮寫 | autic |
| 性質 | |
| 面 | 22 |
| 邊 | 48 |
| 頂點 | 28 |
| 歐拉特徵數 | F=22, E=48, V=28 (χ=2) |
| 組成與佈局 | |
| 面的種類 | 12三角形 5 正方形 5 八边形 |
| 頂點的種類 | 2.4+8(3.82) 4(3.43) 8(3.4.3.8) |
| 對稱性 | |
| 對稱群 | C4v |
| 特性 | |
| convex | |
体积,表面积
棱长为a的侧台塔截角立方体的表面积(A)和体积(V)
参考文献
- 诺曼·约翰逊, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
- Victor A. Zalgaller. . Consultants Bureau. 1969. No ISBN. The first proof that there are only 92 Johnson solids.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.