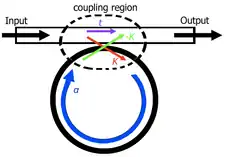
光學環形諧振器

光學環形諧振器由至少一個光路封閉的波導以及光線的輸入與輸出端(比如波導)所組成。光學環形諧振器的概念與迴音廊相仿，不同處在於使用光線，並且需遵守建設性干涉與全內反射條件。當符合共振條件的光線從輸入端波導進入，並經過環形波導，在環形波導裡由於建設性干涉而逐漸增加光強，最後在輸出端波導輸出。

一個用電腦模擬的環形諧振器，輸入光為共振波長的連續波。

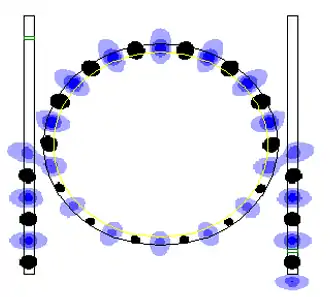
由於只有特定的波長的光才能在環形波導中發生共振，整個光學環形諧振器可視為是一個濾波器。此外，兩個或多個環形波導可以互相耦合，產生出加/減光學濾波器。[1]

背景

壓克力中的全內反射。

光學環形諧振器的原理包含:全內反射、建設性干涉與光學耦合。

全內反射

由於全內反射，光線在光學環形諧振器裡傳播時會留在波導內。當光線打到傳播介質的邊界時，若入射角大於臨界角，且邊界另一側物質的折射率較低，全內反射便會發生，不會有光線通過邊界。為了讓光學環形諧振器良好運作，滿足全反射條件是必要的，應盡可能避免光線離開波導。

干涉

干涉是指兩個或多個波疊加成一個振幅更高或更低的合成波。而在建設性干涉時，兩個相同相位的波會相互干涉出一個振幅為兩波相加的合成波。當光線在繞行環形波導時，它會與其他待在環裡的光線互相干涉。因此，假設系統中沒有吸收、漸逝波、不完美耦合等因素造成的損失，且系統符合共振條件，則光學諧震器輸出的光強將會輸入的光強相同。

圖中的K為耦合係數，t為穿透係數，α為光線在環裡的能量損失。

光學耦合

右圖中，由於漸逝波的效應，當光線從上方的波導經過時，部分的光線會耦合進入環形波導。有三個因素會影響耦合:波導之間的距離、波導之間能耦合的長度、折射率。減少波導間的距離、增加波導之間能耦合的長度都可以增加耦合效率。波導本身的折射率與波導與波導之間物質的折射率也會影響耦合效率。

一個關於耦合特性是臨界耦合(critical coupling)，臨界耦合發生時，經過耦合區後不會有光強存在，所有的光線都會儲存在環型波導裡，並且在環裡耗散。(如頁首圖片所示範)[2]

要讓臨界耦合發生，需要滿足以下公式:

|\mathrm {K} |^{2}+|t|^{2}=\mathbf {1}

其中t是經過耦合區的透射係數， $\mathrm {K}$ 是耦合係數。

理論

要了解光學環形諧振器，要先理解環形諧振器的光程差(OPD)。對於單環的環型諧振器有下式:

\mathbf {OPD} =2\pi rn_{eff}

其中r是環狀波導的半徑， $n_{eff}$ 是波導材質的等效折射率，為了滿足全內反射條件， $n_{eff}$ 必須大於周圍物質的折射率，比如空氣。

為了讓共振發生，需要滿足共振條件:

\mathbf {OPD} =m\lambda _{m}

$\lambda _{m}$ 是共振波長，m代表諧振器的第幾個模態，為正整數。這個公式表明為了讓光線在環裡產生建設性干涉，環的圓周長必須是波長的整數倍。這個特性表示當含有多個波長的光線(如白光)進入諧振器時，只有共振波長的光線可以通過諧振器。

環形諧振器的品質因子(Q因子)與細緻度(finesse)可以用以下公式定量描述 (參見參考資料: eq: 2.37[3],or eq:19+20[4]):

\mathbf {Q} ={\frac {\lambda }{\delta \nu }}

{\mathcal {F}}={\frac {\nu _{f}}{\delta \nu }}

${\mathcal {F}}$ 是諧振器的細緻度， $\lambda$ 是光的波長， $\nu _{f}$ 是輸出光的自由光譜區(FSR, free spectral range)， $\delta \nu$ 是輸出光的半峰全寬(FWHM)。

品質因子可以用來決定任意環形諧振器的共振波長範圍，也可以用來量化諧振器在工作時的能量耗損，較低的Q因子通常代表較高的損耗。

諧振器的輸出光譜，光譜中包含多個共振模態 (m=1, m=2, m=3, ..., m=n) 。

雙環諧振器

一個包含兩個不同半徑的環的雙環諧振器，圖中只展示了光線從輸入到輸出的相對光線強度。光線實際穿過雙環諧振器時，會在環裡進行很多圈的傳播，而不是如圖中表現。

雙環諧震器使用兩個環狀波導，它們可以串聯(如右圖所示)或並聯。串聯時，雙環諧振器的輸出方向與輸入相同。當輸入光符合第一個環的共振條件時，光線耦合進入第一個環，並沿著環傳播。若光線符合第二個環的共振條件，光線會從第一個環耦合到第二個環。依同樣方式，光線最終會耦合到輸出波導。

要讓目標光線能通過雙環諧震器，需要符合下條件:

\ 2\pi n_{1}R_{1}=m_{1}\lambda _{1}

\ 2\pi n_{2}R_{2}=m_{2}\lambda _{2}

$m_{1}$ 與 $m_{2}$ 是第一與第二個環的模態數(mode number)，為正整數。要讓同樣波長的光線穿過整個系統，所以 $\lambda _{1}=\lambda _{2}$ 。

整理後得到:

\ {\frac {n_{1}R_{1}}{m_{1}}}={\frac {n_{2}R_{2}}{m_{2}}}

其中 $m_{1}$ 與 $m_{2}$ 為整數。雙環諧振器可做為可調變的反射濾波器(如右圖)。[5]

應用

由兩個環與一個波導組成的光學反射器。圖中下方波導的綠色箭頭為輸入光，輸入光耦合進入上方的兩個並聯的環型波導，產生逆時針傳播的光(環裡的綠色箭頭)。由於兩個環互相耦合，在兩個環裡都產生順時針傳播的光(環裡的紅色箭頭)，光線最終耦合回到下方波導，產生反射的效果。[5]

由於光學諧振器能過濾特定波長的光線，可以透過使用多個光學諧振器製造出高階數的光學濾波器。光學諧振器有"小尺寸、低損耗、可整合進現存光學系統"的優點。[6]除此之外，由於可以透過改變環的半徑來改變共振波長，整個諧振器可以視為可調變的系統，這個特性可以用來製作某些力學感應器。若諧振器受到應力作用，發生尺寸變化，則光線的共振波長也會跟著改變。這個效果可以用來監測光纖或波導是否發尺寸變化。[7]

除了改變半徑，也可以改變折射率進行調變，比如透過熱、電磁[8]、全光[9](all-optical)效應。電磁與全光效應比起熱與力學反應的更快，適合應用在光通訊裡。

環形、圓柱形和球形的光學諧振器可應用在生物傳感的領域中。[10][11][12][13] 如何增加生物傳感器的性能是其中一個研究重點。使用光學諧振器作為生物傳感器的優點是只需少量的樣品就能測得光譜，並且能大大的減少溶劑和雜質造成的拉曼和螢光訊號。諧振器也被用於氣體的化學鑑定，用來測量吸收光譜。[14]

一些科學家關注於製作高Q因子的三維的球形諧振器，這些介電球"被提議作為低損耗的光學諧振器，用來進行雷射冷卻以研究腔量子電動力學，或者用來檢測單個捕獲原子的超敏感檢測器。"[15]

環形諧振器也可以在量子資訊實驗中作為單光子源。[16] 許多用於製作光學諧振器的材料在高光強下會有非線性效應出現，這些非線性允許四波混頻與自發參量下轉換等頻率調變過程出現，後者可用來生成光量子對。

參見

參考資料

YouTube上的光學環形諧振器的模擬動畫（页面存档备份，存于）

外部連結

Otto; Schwelb. Chremmos, Ioannis , 编. . Springer Series in Optical Sciences 156. Boston, MA: Springer US. 2010. ISBN 9781441917430. doi:10.1007/978-1-4419-1744-7.
Xiao, Min; Jiang, Dong; Yang. . IEEE Journal of Quantum Electronics (44.11, November 2008).
Rabus, Dominik Gerhard. . 2002-07-16 [2021-01-22]. doi:10.14279/depositonce-565. （原始内容存档于2021-01-15）（英语）.
Hammer, Manfred; Hiremath, Kirankumar R.; Stoffer, Remco. . AIP Conference Proceedings. 2004-05-10, 709 (1): 48–71. ISSN 0094-243X. doi:10.1063/1.1764013.
Chremmos, I.; Uzunoglu, N. . IEEE Photonics Technology Letters. 2010, 17 (10): 2110–2112. ISSN 1041-1135. doi:10.1109/LPT.2005.854346.
Ilchenko; Matsko. . IEEE Journal of Selected Topics in Quantum Electronics (12.1, January 2006).
Westerveld, W.J.; Leinders, S.M.; Muilwijk, P.M.; Pozo, J.; van den Dool, T.C.; Verweij, M.D.; Yousefi, M.; Urbach, H.P. . IEEE Journal of Selected Topics in Quantum Electronics. 10 January 2014, 20 (4): 101. Bibcode:2014IJSTQ..20..101W. doi:10.1109/JSTQE.2013.2289992.
Sadasivan, Viswas. . Journal of Lightwave Technology. 2014, 32 (1): 107–114. Bibcode:2014JLwT...32..107S. doi:10.1109/JLT.2013.2289324.
Ibrahim,and, Tarek A.; Grover, Rohit; Kuo, Li-Chiang; Kanakaraju, Subramaniam; Calhoun, Lynn C.; Ho, Ping-Tong. . OSA Trends in Optics and Photonics (Optical Society of America, 2003). 2003: ITuE4. ISBN 978-1-55752-751-6. doi:10.1364/IPR.2003.ITuE4.
A. Ksendzov; Y. Lin. . Opt. Lett. 2005, 30 (24): 3344–3346. Bibcode:2005OptL...30.3344K. doi:10.1364/ol.30.003344.
K. D. Vos; I. Bartolozzi; E. Schacht; P. Bienstman; R. Baets. . Opt. Express 15 (12). 2007: 7610–7615.
Witzens, J.; Hochberg, M. . Optics Express. 2011, 19 (8): 7034–7061. Bibcode:2011OExpr..19.7034W. PMID 21503017. doi:10.1364/OE.19.007034.
Lin S.; K. B. Crozier. . ACS Nano. 2013, 7 (2): 1725–1730. PMID 23311448. doi:10.1021/nn305826j.
Blair; Chen. . Applied Optics (40.4, February 2001).
Götzinger; Benson; Sandoghdar. . Optics Letters (27.2, January 2002).
E. Engin; D. Bonneau; C. Natarajan; A. Clark; M. Tanner; R. Hadfield; S. Dorenbos; V. Zwiller; K. Ohira. . Opt. Lett. 2013, 21 (23): 27826–27834. Bibcode:2013OExpr..2127826E. PMID 24514299. arXiv:1204.4922 . doi:10.1364/OE.21.027826.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Otto; Schwelb. Chremmos, Ioannis , 编. . Springer Series in Optical Sciences 156. Boston, MA: Springer US. 2010. ISBN 9781441917430. doi:10.1007/978-1-4419-1744-7.

[Xiaoetal-2] Xiao, Min; Jiang, Dong; Yang. . IEEE Journal of Quantum Electronics (44.11, November 2008).

[3] Rabus, Dominik Gerhard. . 2002-07-16 [2021-01-22]. doi:10.14279/depositonce-565. （原始内容存档于2021-01-15）（英语）.

[4] Hammer, Manfred; Hiremath, Kirankumar R.; Stoffer, Remco. . AIP Conference Proceedings. 2004-05-10, 709 (1): 48–71. ISSN 0094-243X. doi:10.1063/1.1764013.

[:0-5] Chremmos, I.; Uzunoglu, N. . IEEE Photonics Technology Letters. 2010, 17 (10): 2110–2112. ISSN 1041-1135. doi:10.1109/LPT.2005.854346.

[IlchenkoandMatsko-6] Ilchenko; Matsko. . IEEE Journal of Selected Topics in Quantum Electronics (12.1, January 2006).

[7] Westerveld, W.J.; Leinders, S.M.; Muilwijk, P.M.; Pozo, J.; van den Dool, T.C.; Verweij, M.D.; Yousefi, M.; Urbach, H.P. . IEEE Journal of Selected Topics in Quantum Electronics. 10 January 2014, 20 (4): 101. Bibcode:2014IJSTQ..20..101W. doi:10.1109/JSTQE.2013.2289992.

[8] Sadasivan, Viswas. . Journal of Lightwave Technology. 2014, 32 (1): 107–114. Bibcode:2014JLwT...32..107S. doi:10.1109/JLT.2013.2289324.

[9] Ibrahim,and, Tarek A.; Grover, Rohit; Kuo, Li-Chiang; Kanakaraju, Subramaniam; Calhoun, Lynn C.; Ho, Ping-Tong. . OSA Trends in Optics and Photonics (Optical Society of America, 2003). 2003: ITuE4. ISBN 978-1-55752-751-6. doi:10.1364/IPR.2003.ITuE4.

[10] A. Ksendzov; Y. Lin. . Opt. Lett. 2005, 30 (24): 3344–3346. Bibcode:2005OptL...30.3344K. doi:10.1364/ol.30.003344.

[11] K. D. Vos; I. Bartolozzi; E. Schacht; P. Bienstman; R. Baets. . Opt. Express 15 (12). 2007: 7610–7615.

[12] Witzens, J.; Hochberg, M. . Optics Express. 2011, 19 (8): 7034–7061. Bibcode:2011OExpr..19.7034W. PMID 21503017. doi:10.1364/OE.19.007034.

[13] Lin S.; K. B. Crozier. . ACS Nano. 2013, 7 (2): 1725–1730. PMID 23311448. doi:10.1021/nn305826j.

[BlairandChen-14] Blair; Chen. . Applied Optics (40.4, February 2001).

[Gotzingeretal-15] Götzinger; Benson; Sandoghdar. . Optics Letters (27.2, January 2002).

[16] E. Engin; D. Bonneau; C. Natarajan; A. Clark; M. Tanner; R. Hadfield; S. Dorenbos; V. Zwiller; K. Ohira. . Opt. Lett. 2013, 21 (23): 27826–27834. Bibcode:2013OExpr..2127826E. PMID 24514299. arXiv:1204.4922 . doi:10.1364/OE.21.027826.