開普勒方程
開普勒方程(英語:)把軌道力學中受到連心力影響的軌道中天體多種幾何性質聯繫起來。
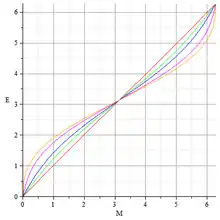
這條方程最早由約翰內斯·開普勒得出,推導過程見於他在1609年出版的著作《新天文學》的第60章[1][2],而他在著作《哥白尼天文學概要》(1621年出版)的第五卷中還提出了此方程的一個迭代解[3][4]。這條方程在物理學史和數學史上都扮演着重要的角色,特別是在古典天體力學史上。
方程
開普勒方程如下:
偏近點角E對於計算開普勒軌道上移動點的位置相當有用。比方說,天體在座標x = a(1 − e)、y = 0和時間t = t0時經過近星點,那麼要找出天體在任意時間的位置的話,首先可由時間和平均運動n用方程M = n(t − t0)計算出平近點角M,然後解上述的開普勒方程得E,便能由下列方程求座標:
其他形式
開普勒方程共有幾種形式。每一種形式都同一種特定軌道類型有關。標準的開普勒方程用於橢圓軌道(0 ≤e<1)。雙曲開普勒方程用於雙曲軌跡(e≫1)。徑向開普勒方程用於線性(徑向)軌跡 (e=1)。抛物線軌跡(e=1)則用巴克方程。
當e = 0時,軌道是圓形的。增加e會導致圓形變成橢圓。當e = 1時共有三種可能性:
- 抛物線軌跡;
- 沿着從吸引中心起始無限長射線向內或向外的軌跡;
- 或沿着由吸引中心和距其一定距離的點所形成的線段來回移動的軌跡。
把e從1輕微增加會形成轉角剛好低於180度的雙曲軌道。繼續增加數值會導致轉角變小,而當e趨向無限時,軌道則變成長度無限的直線。
徑向開普勒方程
徑向開普勒方程如下:
其中t與時間成正比,而x則與射線上與吸引中心的距離成正比。下式是通過把開普勒方程成1/2並把e定為1而成:
- 。
代入得
- 。
逆問題
可以利用已知的E值直接求出M。但用已知M值來求E卻要複雜得多。因為不存在解析解。
可以使用拉格朗日反算法寫出開普勒方程解的級數表達式,但所有e和M的組合都不能使級數收斂(見下文)。
文獻中對開普勒方程可解性的混淆已存在了四個世紀[5]開普勒本人曾對找得到通解的可能性表示懷疑。
| 對於它[開普勒方程]不能用演繹法求解這點我是足夠滿意的,因為弧和正弦之間有着本質上的差異。但若果我錯了的話,任何人都應該給我指出來,而那個人在我眼中就是偉大的阿波羅尼奧斯。 | ||
| ——約翰內斯·開普勒[6] | ||
逆開普勒方程
逆開普勒方程是所有實數值的開普勒方程解:
展開得:
以上的級數可用Wolfram Mathematica的InverseSeries運算得出。
InverseSeries[Series[M - Sin[M], {M, 0, 10}]]InverseSeries[Series[M - e Sin[M], {M, 0, 10}]]
這些函數只是簡單的麥克勞林級數。這樣的超越函數泰勒級數寫法可被視為那些函數的定義。因此,這個解是逆開普勒方程的正式定義。然而,在e非零的時候,E並不是M的整函數。其導數
在e<1時於無限複數集合中趨向零。在有解,而在這些值時
(其中逆cosh取正值),而dE/dM在這些點則趨向無限。這意味着此麥克勞林級數的收歛半徑為,並且當M比這大時級數不會收歛。此級數還可用於雙曲情況,此時其收歛半徑為。當e=1時此級數只在M<2π時收歛。
還可以寫出用e冪表示的麥克勞林級數。這級數在e大於拉普拉斯極限(約為0.66)時不會收歛,與M值無關(除非M為2π的倍數),但若e小於拉普拉斯極限時則級數在任何M值時都會收歛。級數的係數除了第一個之外(只是M而已),都與M成週期式關係,週期為2π。
逆徑向開普勒方程
逆徑向開普勒方程(e = 1)可被寫成:
展開得:
上述結果可用Wolfram Mathematica求得:
InverseSeries[Series[ArcSin[Sqrt[t]] - Sqrt[(1 - t) t], {t, 0, 15}]]
逆問題的數值近似
逆問題在大部份的應用中都能以數值方法求得函數的根:
可以經牛頓法來進行迭代:
注意在這個計算E和M的單位是弧度角。重覆迭代直到已經達到想要的準確度(例如,當f(E) < 所需的準確度)。對大部份的橢圓軌道而言,起始值取E0 = M(t) 已經足夠。而對e > 0.8的軌道而言,則應取起始值{{{1}}}。相近的手法還可以用於開普勒方程的雙曲形式[7]:66-67。而在面對抛物線軌跡的個案時則使用巴克方程。
定點迭代
另一種有關的解法由考慮開始。重覆地將E的值代入右方式子就能得到簡單的求的定點迭代算法。此方法與開普勒1621年的解相同[4]。
function E(e,M,n)
E = M
for k = 1 to n
E = M + e*sin E
next k
return E
迭代次數取決於的數值。雙曲形式則用相近的。
這個方法與上文牛頓法解的關係如下:
若及的數值小的話,取一次項得近似:
- 。
另見
- 開普勒定律
- 開普勒問題
- 廣義相對論中的開普勒問題
參考資料
- Kepler, Johannes. . . 1609: 299–300 [2018-09-06]. (原始内容存档于2019-06-11) (拉丁语).
- Aaboe, Asger. . Springer. 2001: 146–147. ISBN 978-0-387-95136-2.
- Kepler, Johannes. . . 1621: 695–696 [2018-09-06]. (原始内容存档于2019-06-19) (拉丁语).
- Swerdlow, N. M. . Journal for the History of Astronomy. 2000, 31: 339–341 [2018-09-06]. Bibcode:2000JHA....31..339S. doi:10.1177/002182860003100404. (原始内容存档于2019-07-12).
- 開普勒方程常被聲稱“沒有解釋解”;例子見這裏 (页面存档备份,存于)。至於這是否真確取決於是否認為無限級數(或不一定收歛的級數)算解釋解。也有其他作者無理地聲稱此方程無解;例子見M. V. K. Chari, Sheppard Joel Salon 2000 Technology & Engineering.
- "Mihi ſufficit credere, ſolvi a priori non poſſe, propter arcus & ſinus ετερογενειαν. Erranti mihi, quicumque viam monſtraverit, is erit mihi magnus Apollonius." (页面存档备份,存于) Hall, Asaph. . Annals of Mathematics. May 1883, 10 (3): 65–66. doi:10.2307/2635832.
- Pfleger, Oliver Montenbruck, Thomas. Third edition. Berlin, Heidelberg: Springer Berlin Heidelberg. 1998. ISBN 978-3-662-03349-4.
外部連結
| 维基共享资源上的相关多媒体资源:開普勒方程 |
- Danby, J. M.; Burkardt, T. M. . Cel. Mech. 1983, 31: 95–107. Bibcode:1983CeMec..31...95D. doi:10.1007/BF01686811.
- Conway, B. A. . 1986. doi:10.2514/6.1986-84.
- Mikkola, Seppo. . Cel. Mech. 1987, 40 (3). Bibcode:1987CeMec..40..329M. doi:10.1007/BF01235850.
- Fukushima, Toshio. . Cel. Mech. Dyn. Astron. 1996, 66 (3): 309–319. Bibcode:1996CeMDA..66..309F. doi:10.1007/BF00049384.
- Charles, E. D.; Tatum, J. B. . Cel. Mech. Dyn. Astr. 1997, 69 (4): 357–372. Bibcode:1997CeMDA..69..357C. doi:10.1023/A:1008200607490.
- Stumpf, Laura. . Cel. Mech. Dyn. Astr. 1999, 74 (2): 95–109. doi:10.1023/A:1008339416143.
- Palacios, M. . J. Comp. Appl. Math. 2002, 138: 335–346. Bibcode:2002JCoAM.138..335P. doi:10.1016/S0377-0427(01)00369-7.
- Boyd, John P. . Appl. Num. Math. 2007, 57 (1): 12–18. doi:10.1016/j.apnum.2005.11.010.