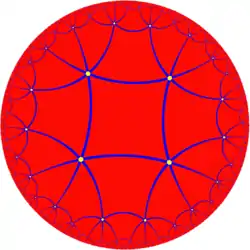
六階正方形鑲嵌

在幾何學中， 六階正方形鑲嵌是由正方形組成的雙曲面正鑲嵌圖，每六個正方形共用一個頂點。在施萊夫利符號用{4,6}表示。六階正方形鑲嵌即每個頂點皆為六個正方形的公共頂點，頂點周圍包含了六個不重疊的正方形，一個正方形內角90度，六個正方形超過了360度，因此無法因此無法在平面作出，但可以在雙曲面上作出。

六階正方形鑲嵌
六階正方形鑲嵌
龐加萊圓盤模型
類別雙曲正鑲嵌
對偶多面體四階六邊形鑲嵌
識別
鮑爾斯縮寫
hisquat在维基数据编辑
數學表示法
考克斯特符號
node 6 node 4 node_1 
施萊夫利符號{4,6}
威佐夫符號
6 | 4 2
組成與佈局
頂點圖46
對稱性
對稱群[6,4], (*642)
特性
點可遞、 邊可遞、 面可遞
圖像

四階六邊形鑲嵌
（對偶多面體）

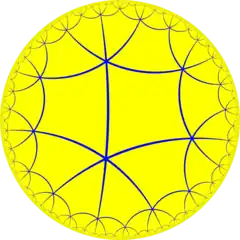
對稱性

這個鑲嵌代表一個雙曲的四次反射萬花筒。 這由四個三階交叉反射性在軌型符號被稱為(*3333)。 在考斯特表示法可表示為[6,4*], 從三個鏡射線當中移除兩條穿過正方形中心的鏡射線。 *3333對稱性可透過加入平分基本域的鏡射線增倍成663對稱性。

這個交錯塗色的正方形鑲嵌顯示了奇數/偶數的反射對稱群。 這個雙色鑲嵌的wythoff構建為t1{(4,4,3)}。而六色鑲嵌對稱群可由六邊形對稱群構造出來。

[4,6,1+] = [(4,4,3)] 或 (*443) 對稱性
node_1 4 node 6 node_h0  = node_1 split1-44 branch 		 [4,6*] = (*222222) 對稱性
node_1 4 node_g 6sg node_g  = branchu_11 2 branchu_11 2 branchu_11 


相關的多面體與鑲嵌


多面体 欧式镶嵌 双曲镶嵌

{4,2}
node_1 4 node 2 node 
{4,3}
node_1 4 node 3 node 
{4,4}
node_1 4 node 4 node 
{4,5}
node_1 4 node 5 node 
{4,6}
node_1 4 node 6 node 
{4,7}
node_1 4 node 7 node 
{4,8}
node_1 4 node 8 node 		 ...
{4,∞}
node_1 4 node infin node 

參見
维基共享资源中相关的多媒体资源：六階正方形鑲嵌

參考資料
    • John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
    • . . Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.

    外部連結
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.