出入相补
出入相补(又称以盈补虚)积是古中国数学中一条用于推证几何图形的面积或体积的基本原理。其内容有四;
- 一个几何图形,可以切割成任意多块任何形状的小图形,总面积或体积维持不变=所有小图形面积或体积之和。
- 一个几何图形,可以任意旋转,倒置、移动、复制,面积或体积不变。
- 多个几何图形,可以任意拼合,总面积或总体积不变。
- 几何图形与其复制图形拼合,总面积或总体加倍。
出入相补原理最早由三国时代魏国数学家刘徽创建。“勾股各自乘,并,而开方之,即弦。勾自乘为朱方,股自乘为青方,另出入相补,各从其类,因就其余不移动也,合成弦方之幂,开方除之,即弦也。”[1]
等腰三角形面积

- 《九章算术·方田》第25问:“今有圭田,广十二步,正纵二十一步。问为田几何?
- 答曰:一百二十六步。”
- 《九章算术·方田》第26问:“又有圭田,广五步二分步之一,纵八步三分步之二。问:为田几何?”
- 答曰:二十三步六分步之五。
- 术曰:半广以乘正纵。
圭田指等腰三角形田。《九章算术》给出求圭田面积的公式:
圭田面积=半广以乘正纵。半广=等腰三角形底长之半,正纵指等腰三角形的高。
- 等腰三角形面积= x 等腰三角形底长x等腰三角形的高。
刘徽从出入相补予以证明:
刘徽注曰:半广者以盈补虚为直田也。亦可半正纵以乘广。按半广乘纵,以取中平之数。故广纵相乘为积步。
如图ABC 为等腰三角形田,BC 为等腰三角形底宽(广),DC 为 半广 = ,AD 为等腰三角形的高(正纵)。
以盈补虚为直田:将三角形ABC按中线等分为两个相等的三角形ABD,ADC。将实三角形ABD 经平移和1800 转动,填补虚三角形ADC,成为一个长方形AECD。三角形ABC的面积=长方形AECD的面积=DC(半广) x AD(正纵)。 圭田面积=半广以乘正纵=DC x AD。
第二法:从三角形ABC底线作长方形BCFE,其高度BE= 三角形高度AD/2。从三角形顶点A作垂直平分线AD,与长方形顶线EF相交于M点。将盈三角形AML移动,补上虚三角形CFL,将盈三角形AMK移动,补上虚三角形BEK,即得实长方形EFCB。所以三角形ABC的面积=长方形EFCB面积=半正纵以乘广。
任意三角形面积
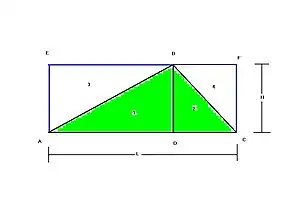
如图三角形ABC底长为L,高为H,求三角形面积。
- 从B点画垂直线BD,将三角形ABC切割成两个直角三角形ABD、BCD
- 复制三角形ABD为ABE,倒置其上:
- 复制三角形BCD为BCF,倒置其上:
- 长方形ACFE面积=三角形1,2,3,4之和,
- 但三角形3面积=三角形1面积,三角形4面积=三角形2面积,
- 所有长方形ACFE面积=HxL=2X(三角形1+三角形2)=2X三角形ABC,
- 所有三角形ABC面积= HxL/2。
直角梯形面积
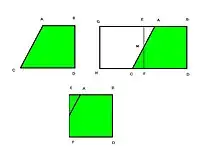
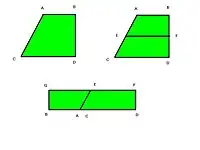
《九章算术·方田》第27问
- 今有邪田一头广三十步,一头广四十二步,正纵六十步。问,为田几何?
- 答曰:九亩一百四十四步
- 《九章算术·方田》第28问:
- 又有邪田,正广六十五步,一畔纵一百步,一畔纵七十二步。问,为田几何?
- 答曰:二十三亩七十步。
- 术曰:并两邪而半之,以乘正纵若广。又可半正纵若广,以并,亩法而一。
邪田即斜田,即一边直角一边斜的梯田。如图邪田ABCD。求面积时将两个邪田合併,成为一个长方形GBHD,从长方形正中作垂直线平分EF,将长方形等分为二。将盈三角形MCF移补虚三角形MAE,得实长方形EBFD。
由于以盈补虚,邪田ABCD面积=长方形EBFD面积=邪田正纵x(邪田上边长度+邪田下边长度)/2。
第二种方法:“又可半正纵若广,以并”:在邪田正纵中点作平行线EF;将上半部ABEF与下半步EFCD合併,成为长方形。
邪田ABCD面积=长方形GFDB面积=(AB+CD)*FD=(AB+CD)*BD/2。
梯形面积
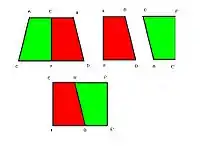
《九章算术方田》第29问:
- 今有箕田,舌广二十步,踵广五十步,正纵一百三十五步。问:为田几何?
- 答曰:四十六亩二百三十二步半。
- 术曰:并踵舌而半之,以乘正纵。亩法而一。
- 刘徽注曰:中分箕田则为两邪田,故其术相似。又可并踵舌,半正踵以乘之。
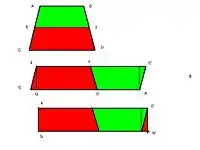
箕田即正梯形田。 第一法: 将梯田ABCD就正中线截为两个邪田EBDF和AECF,将AECFD倒转移动到右边,与EBDF合并成为长方形EF'E'F。梯田ABCD面积=长方形EF'E'F面积=((梯田上边长度+梯田下边长度)/2) X 梯田高度。
第二法:将梯田ABCD就半高处作水平线EF,将ABCD截为两个梯形ABFE,EFDC。将上截ABFED倒转,和EFDC合并为四边形EE'AC,再从左边截出三角形ECG,移动到右边,并成长方形EE'G'G。 梯田ABCD面积=长方形EE'G'G面积=(梯形上边长度+梯形下边长度) * 梯形高度之半。
内接正十二边形面积

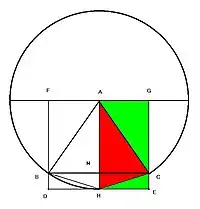
刘徽计算圆形内接正十二边形面积的公式:“以六觚之一面乘半径,因而三之,得十二觚之幂”。
如图 BC为内接正六边形的一边,HC为正十二边形的一边,圆的半径为AH。
- 刘徽公式: 以内接六边形一边BC 的长度 X 圆的半径AH X 3=内接正十二边形面积。
- 如圆半径=1,则内接正十二边形面积=3
利用出入相补容易证明刘徽公式。
- 作长方形FGED, 其面积= BC x AH。
- 用三角形AHC补虚三角形AGC,又以三角形CMH补虚三角形CEH,得正方形AGEH,
- 正方形AGEH面积=两个三角形AHC面积。
- 因此长方形FGED面积=2X 正方形AGEH面积=4X三角形AHC面积。
- 内接正十二边形面积=12 X三角形AHC 面积 = 3 X 方形FGED面积 =3X 正六边形边长 X 半径。
推广为 圆内接2N 边形的面积 = x半径 x N边形一边的长度。
刘徽还计算出半径一尺圆形内接正96边形面积=313.9344方寸,内接正192边形面积=314.1024方寸
梯形立体体积
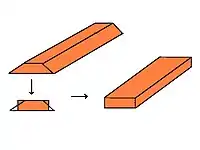
《九章算术》卷第五商功:“今有堤下广二丈,上广八尺,高四尺,袤一十二丈七尺。问:积几何?”
刘徽术文:“并上下广而半之者,以盈补虚,得中平之广,以高若深乘之,得一头之立幂,又以袤乘之,得立实之积。”