分位圖

分位圖（quantile-quantile plot）又稱QQ圖（Q-Q plot，Q代表分位数），在统计学中是比较两个概率分布的分位数，來比較这两个概率分布的概率图方法。首先选定分位数的对应概率区间集合，在此概率区间上，点(x,y)对应于第一个分布的一个分位数x和第二个分布在和x相同概率区间上相同的分位数。因此画出的是一条含参数的曲线，参数为概率区间的分割数[1] 。

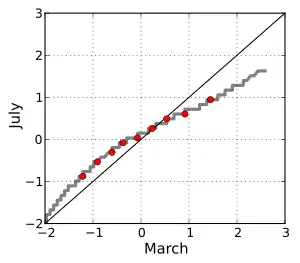
一份比較不同月分間，日平均氣溫的圖

如果被比较的两个分布比较相似，则其分位圖近似地位于y = x上。如果两个分布线性相关，则分位图上的点近似地落在一条直线上，但并不一定是y = x。分位图同样可以用来估计一个分布的位置参数。

分位图可以比较概率分布的形状，从图形上显示两个分布的位置，尺度和偏度等性质是否相似或不同。它可以用来比较一组数据的经验分布和理论分布是否一致。[2]另外，分位图也是一种比较两组数据背后的随机变量分布的非参数方法。一般来说，当比较两组样本时，分位圖是一种比直方图更加有效的方法，但是理解分位图需要更多的背景知识。